6. Базовая графика. Аффинные преобразования

6.1. Однородные координаты

Основное применение однородных координат – это геометрические преобразования, поскольку при помощи троек однородных координат и матриц третьего порядка можно описать любое аффинное преобразование плоскости. Аналогично, с помощью четверок однородных координат и матриц четвертого порядка можно описать любое преобразование в пространстве [16, 24].

В однородных координатах точка Р(x,y) записывается как Р(Wx,Wy,W) для любого масштабного множителя W0. При этом если для точки задано ее представление в однородных координатах Р(X,Y,W), то можно найти ее двумерные декартовы координаты как x=X/W и y=Y/W.

Геометрический смысл однородных координат заключается в следующем (рис.6.1). Произвольная точка на прямой, соединяющей начало координат, точку О(0,0,0), с точкой Р'(x,y,1), может быть задана тройкой чисел вида (Wx,Wy,W). Вектор с координатами Wx,Wy,W является направляющим вектором прямой, соединяющей точки О(0,0,0) и Р'(x,y,1). Эта прямая пересекает плоскость z=1 в точке (x,y,1), которая однозначно определяет точку (x,y) координатной плоскости x,y.

Рис.6.1. Графическое представление однородных координат

Тем самым между произвольной точкой с координатами (x,y) и множеством троек чисел вида (Wx,Wy,W), W0 устанавливается взаимно однозначное соответствие, позволяющее считать числа Wx,Wy,W новыми координатами этой точки.

6.2. Аффинные преобразования на плоскости

Определение 6.1. Аффинные преобразования на плоскости - преобразования, обладающие следующими свойствами:

- любое аффинное преобразование может быть представлено как последовательность операций из числа простейших: сдвиг, растяжение/сжатие, поворот;

- сохраняются прямые линии, параллельность прямых, отношение длин отрезков, лежащих на одной прямой, и отношение площадей фигур.

Общий вид аффинного преобразования на плоскости имеет вид:

,

где , , , , ,  - произвольные числа.

Основные матрицы двумерных аффинных преобразований:

Матрица вращения	Матрица переноса
Матрица масштабирования	Матрица отражения
	.

6.3. Аффинные преобразования в пространстве

Определение 6.2 Аффинные преобразования в пространстве - преобразования, обладающие следующими свойствами:

- любое аффинное преобразование может быть представлено как последовательность операций из числа простейших: сдвиг, растяжение/сжатие, поворот;

- сохраняются параллельность плоскостей, параллельность прямых, параллельность прямой и плоскости.

При замене тройки координат (x, y, z) на четверку (x, y, z, 1) возможно воспользоваться матричной записью в более сложных трехмерных задачах. Любое аффинное преобразование в трехмерном пространстве может по аналогии быть представлено в виде суперпозиции вращений, растяжений и переносов.

Соответственно, матрицы вращения, масштабирования и переноса в пространстве имеют вид:

, ,

, , .

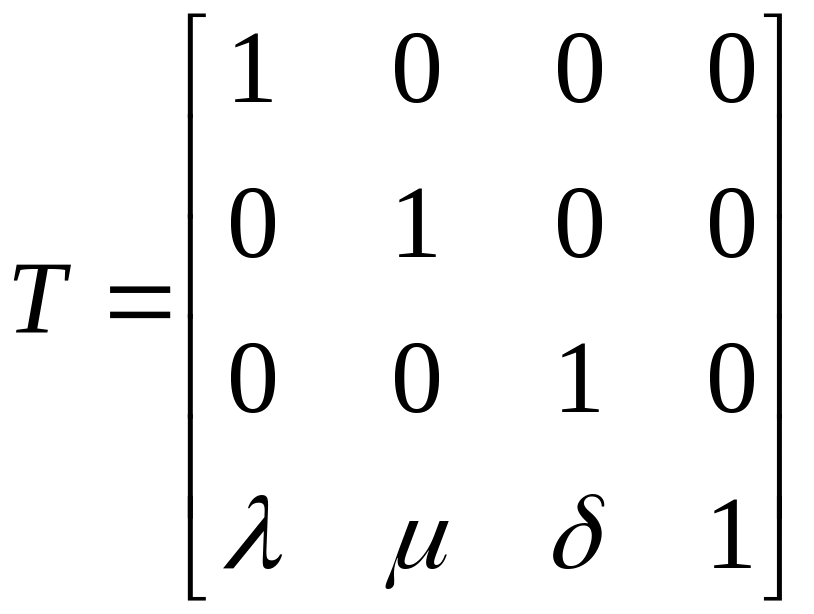При положительном угле  производится вращение против часовой стрелки.