
- •1 Теоретические основы автоматизации
- •Виды систем автоматического управления.
- •2 Линеаризация нелинейных дифференциальных уравнений
- •3 Передаточная функция
- •4 Переходная, импульсная хар-ка
- •5 Частотные характеристики
- •6 Характеристики дифференцирующего и интегрирующего звеньев.
- •7. Характеристики инерционного (апериодического) звена.
- •8 Характеристики инерционно-дифференцирующего звена.
- •9.Звено постоянного запаздывания.
- •Передаточная функция
- •10. Характеристики форсирующего звена.
- •11.Последовательное и параллельное соединение звеньев.
- •12.Простейшие типовые звенья на операционных усилителях.
- •13. Принципы построения динамических звеньев со сложными передаточными функциями на операционных усилителях (тау)
- •14. Критерий Рауса
- •15. Критерий Гурвица
- •16. Критерий Михайлова
- •17 Критерий Найквиста
- •18. Запасы устойчивости
- •21. Ошибки регулирования
- •22. Прямые показатели качества
- •23. Корневые методы оценки качества
- •24 Определение показателей качества по афчх сау
- •25 Оценка сау по показателю колебательности
- •26 Оценка качества по лачх
- •27 Интегральные методы оценки качества
- •28 Коррекция свойств сау изменением коэффициента усиления
- •29 Коррекция свойств сау изменением постоянной времени звена
- •30 Типовые законы регулирования
6 Характеристики дифференцирующего и интегрирующего звеньев.
Интегрирующее звено
Выполняет операцию интегрирования входного сигнала
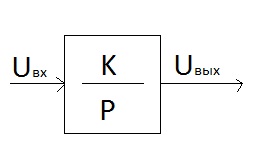
W(p)=K/P

Переходная характеритика




АФЧC

P(w)=0 → BЧХ
Q(w)= → МЧХ
→ МЧХ
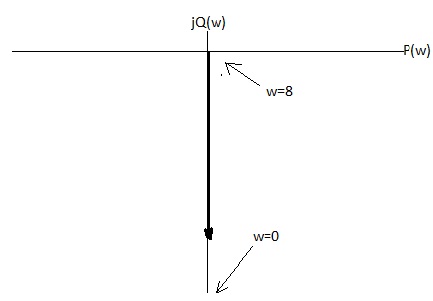
Годограф совпадает с отрицательной мнимой осью.
АЧХ

ФЧХ

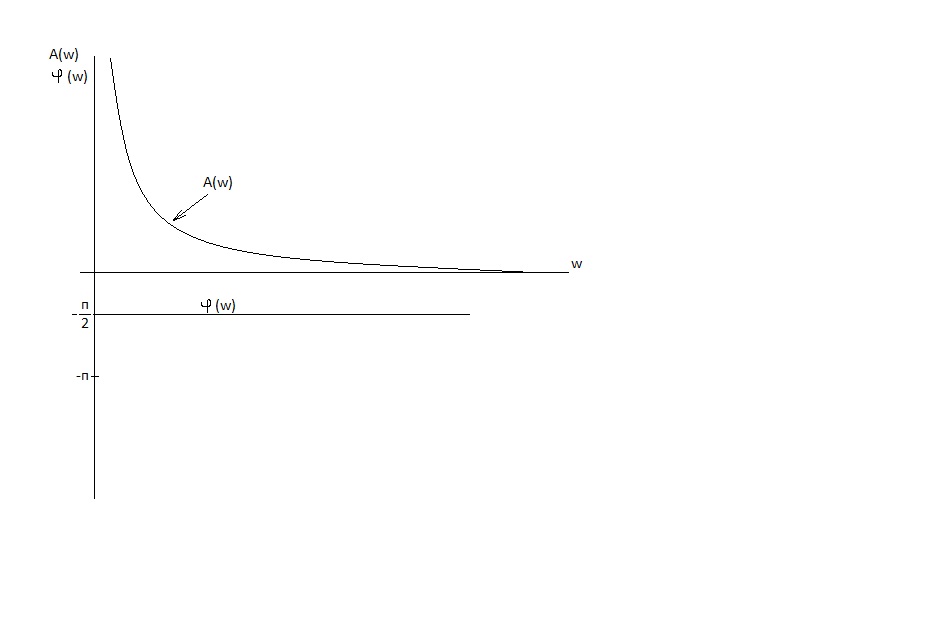
Интегратор
ослабляет высокие частоты и неограниченно
усиливает низкие, фазовый сдвиг постоянен
и равен

ЛАЧХ


ДИФФЕРЕНЦИРУЮЩЕЕ ЗВЕНО
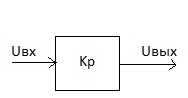
W(p) = KP
Uвых=
Переходная
Переходная характеристика дифференционного звена – импульсная функция, равная бесконечности при t=0/

Частотная характеристика АФЧХ

Вещественная частотная характеристика (ВЧХ):

Мнимая частотная характеристика (МЧХ):


АЧХ

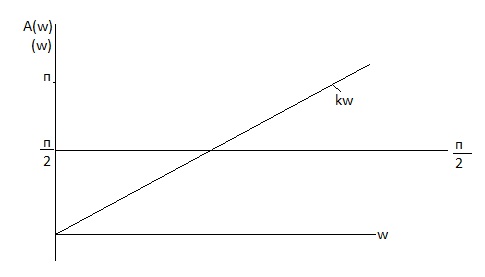
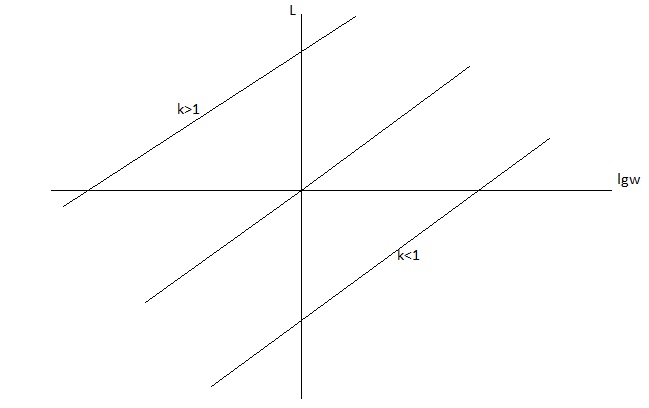
Наклон:

Идеальное дифференцирующее звено не может быть реализовано на реальных физических элементах.
7. Характеристики инерционного (апериодического) звена.







Переходная характеристика
 ,
по табл.
,
по табл.

 Определить
переходную характеристику можно с
помощью так называемой формулы разложения,
иногда называемая формула Хевисайда.
Она
применима для передаточных функций
вида
Определить
переходную характеристику можно с
помощью так называемой формулы разложения,
иногда называемая формула Хевисайда.
Она
применима для передаточных функций
вида


 - корни характерного уравнения(знаменателя)
- корни характерного уравнения(знаменателя)

 ;
;

 В
автоматике принято считать время
переходного процесса по достижении
5%-й окрестности установившегося значения.
В
автоматике принято считать время
переходного процесса по достижении
5%-й окрестности установившегося значения.

Время переходного процесса оценивается по максимальной из постоянных времени, входящий в передаточную функцию, т.е. учитывается главная постоянная времени и вся сложная система аппроксимируемая инерционным звеном, поскольку все постоянные времени к этому моменту уже затухнут.
АФЧХ

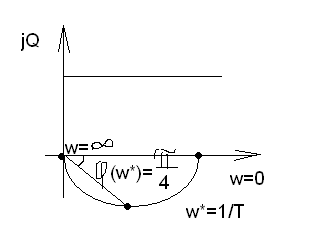
ВЧХ:

МЧХ: 
w* - частота сопряжения

Годограф
при изменении частоты от 0 до
 представляет собой полуокружность в
4-м квадранте с наинизшей точкой по
частоте сопряжения w*.
При этом фазовый сдвиг составляет
представляет собой полуокружность в
4-м квадранте с наинизшей точкой по
частоте сопряжения w*.
При этом фазовый сдвиг составляет
 ,
а коэффициент усиления на частоте
сопряжения
,
а коэффициент усиления на частоте
сопряжения
 .
.
АЧХ

Ф
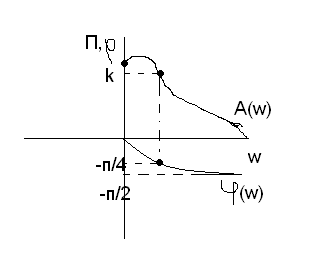 ЧХ
ЧХ

ЛАЧХ

Для упрощения использования ЛАЧХ вводит понятия асимптотических.
Выделяют 2 области частот:
- область низких частот
- область высоких частот
Границы этих областей – частота сопряжения.
А)
обл. НЧ:
 -
горизонтальная прямая
-
горизонтальная прямая
Б)
обл. ВЧ:
 - прямая с наклоном -20 дБ/дек
- прямая с наклоном -20 дБ/дек

Максимальная ошибка – это погрешность замены истинной характеристики на асимптотич. Приходится на част. Сопряж. w*

Уровень -3дБ принято считать границей полосы пропускания.

8 Характеристики инерционно-дифференцирующего звена.
Это звено не является типовым и часто называется реальным дифференциальным звеном. Основные причины использования идеально диф-звено реально не реализуются.


П
 ереходная
характеристика
ереходная
характеристика




АФЧХ

ВЧХ:

МЧХ:
Годограф
описывает полуокружность с радиусом
 при
при
 .
При этом годограф прижим. к положительной
мнимой полуоси и становится практически
неотличим от реального диф. звена.
.
При этом годограф прижим. к положительной
мнимой полуоси и становится практически
неотличим от реального диф. звена.

Частота
 считается
максимальной частотой, при которой
реализуется диф. звено, работающее почти
как идеальное.
считается
максимальной частотой, при которой
реализуется диф. звено, работающее почти
как идеальное.
АЧХ

4. ФЧХ

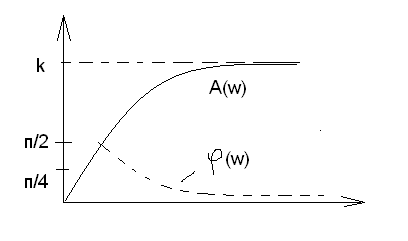
5. ЛАЧХ

А)
обл. НЧ:
 -
прямая с наклоном +20 дБ/дек
-
прямая с наклоном +20 дБ/дек
Б)
обл. ВЧ:
 - горизонтальная прямая
- горизонтальная прямая


