Лекция 29

Основные параметры сигналов с частотной и фазовой модуляцией (ЧМ и ФМ). Сходство и различия сигналов с ЧМ и ФМ. Спектр и занимаемая полоса частот. Сравнительные характеристики устройств и систем с ЧМ и ФМ. Основной метод осуществления ФМ. Фазовый модулятор. Прямой и косвенный методы ЧМ, схемы осуществления и их сравнительные характеристики. Частотный модулятор. Двухтактный частотный модулятор. Частотное и фазовое телеграфирование (ЧТ и ФТ).

Основные параметры сигналов с частотной и фазовой модуляцией (ЧМ и ФМ)

При амплитудной модуляции (АМ) модулирующий сигнал воздействует на амплитуду колебания высокой частоты. Остальные параметры высокочастотного колебания, как-то частота и начальная фаза остаются без изменений.

При частотной модуляции (ЧМ) в соответствии с законом передаваемого сигнала s(t) изменяется частота,¹значение которой определяется из соотношения

, (29.1)

где – частота колебания при отсутствии модулирующего сигнала;k– коэффициент пропорциональности.

При фазовой модуляции (ФМ) в соответствии с законом передаваемого сигнала s(t) изменяется начальная фаза колебания

, (29.2)

где – начальная фаза колебания при отсутствии модулирующего сигнала, которая может быть принята равной нулю. В этом случае, соответственно

.

При рассмотрении общих положений ЧМ и ФМ удобно воспользоваться выражением для гармонического колебания, записанном в следующем виде, например, для тока

, (29.3)

где – фаза колебания, изменяющаяся в общем случае по некоторому закону.

При отсутствии ЧМ или ФМ фаза колебания

, (29.4)

где ω=ω₀– круговая частота колебания, являющаяся постоянной;– начальная фаза колебания.

При ЧМ согласно (29.1) изменяется мгновенная частота колебания в соответствии с модулирующим сигналом. Однако это вовсе не означает, что для записи выражения ЧМ колебания на основании (29.3) следует в (29.4) на место частоты поставить выражение (29.1). При такой подстановке получится выражение, не имеющее физического смысла.

По определению круговая частота колебания есть скорость изменения фазы колебания

.

В общем случае при произвольном изменении фазы колебания последнее выражение определяет мгновенную частоту, то есть

. (29.5)

В свою очередь,

, (29.6)

где – в данном случае постоянная интегрирования, соответствующая начальной фазе колебания.

Учитывая соотношения (29.1), (29.2), (29.5), (29.6), в соответствии с (29.3) можно записать следующие выражения:

• для ЧМ колебания

• для ФМ колебания

.

Амплитуда колебания при ЧМ и ФМ остаётся неизменной.

Если передаваемый (модулирующий) сигнал гармонический, то есть

,

где S– амплитуда сигнала;– круговая частота модулирующего сигнала (для сокращения записи начальная фаза модулирующего сигнала принята равной нулю), то

• при ЧМ

(29.7)

(29.8)

, (29.9)

• при ФМ

(29.10)

(29.11)

. (29.12)

Согласно (29.7) величина при ЧМ определяет максимальное отклонение частоты от среднего значения, называемое девиацией частоты. При ФМ величина, как следует из (29.10), определяет максимальное отклонение (девиацию) начальной фазы. Отношениепри ЧМ называется индексом частотной модуляции, измеряемым в радианах. Обычно обозначается символом. Таким образом, при ЧМ

.

Сравнивая выражения (29.9) и (29.12) для ЧМ и ФМ колебаний соответственно, нетрудно видеть их большое сходство. Кроме того, если при ФМ девиацию начальной фазы также обозначить символом, то есть, и учесть, что функции синуса и косинуса отличаются только сдвигом по фазе на 90⁰, то для ЧМ и ФМ колебаний можно пользоваться одной формой записи, например, как для ЧМ колебания (29.9):

, (29.13)

которой мы в дальнейшем и будем придерживаться.

Большое сходство ЧМ и ФМ колебаний обусловлено тем, что в обоих случаях изменяется фаза колебания и при модуляции гармоническим сигналом не представляется возможным определить вид модуляции: частотная или фазовая. Поэтому обе эти модуляции объединяют под общим названиемугловой модуляции. В то же время этим видам модуляции присущи и некоторые различия изменения фазы колебания, обусловленные разными соотношениями между изменениями начальной фазы и частоты при одинаковом модулирующем сигнале.

При ЧМ девиация частоты прямо пропорциональна амплитуде модулирующего сигнала

и не зависит от частоты модуляции . В то же время индекс ЧМ

,

определяющий, как видно из (29.8), максимальное отклонение (девиацию) фазы при ЧМ, обратно-пропорционален частоте модулирующего сигнала.

При ФМ максимальное отклонение начальной фазы прямо пропорционально амплитуде модулирующего сигнала и не зависит от его частоты, то есть

.

По аналогии с ЧМ параметр называют индексом ФМ.

Частота колебания при ФМ, определяемая на основании соотношений (29.5), (29.11),

.

Согласно последнему выражению девиация частоты при ФМ оказывается прямо-пропорциональной амплитуде модулирующего сигналаS, как и при ЧМ, и прямо пропорциональной частоте модулирующего сигнала, в отличие от ЧМ, и равна

.

На рис.29.1 показаны зависимости девиации частоты и девиации фазыпри ЧМ и ФМ в зависимости от частоты модуляции.

Различное изменение девиации частоты и девиации фазыпри ЧМ и ФМ при изменении амплитуды и частоты модулирующего сигнала даёт возможность определить вид модуляции: частотная (ЧМ) или фазовая (ФМ). Для этого необходимо осуществить модуляцию поочерёдно двумя гармоническими сигналами равной амплитуды, но разных частот. Если отклонение (девиация) начальной фазы неизменно, то модуляция фазовая (ФМ), если отклонение (девиация) начальной фазы обратно пропорционально частоте модулирующего сигнала, то модуляция частотная (ЧМ). Аналогично, если девиация частоты неизменна, то модуляция частотная (ЧМ), если девиация частоты прямо пропорциональна частоте модулирующего сигнала, то модуляция фазовая (ФМ).

Если ЧМ или ФМ осуществляется сложным сигналом

,

то аналитическая запись ЧМ и ФМ колебания (29.13) принимает вид

,

где при ЧМ ипри ФМ.

При различных применениях в радиовещании ЧМ и ФМ обычно удовлетворяются условия:

.

В радиопередающих устройствах с ЧМ характерными данными являются: максимальное отклонение (девиация) частоты и индекс частотной модуляции, под которым подразумевается отношение

, (*)

где F_МАКС– максимальная рабочая частота модуляции.

Так как при ЧМ не зависит от частоты модуляции, то, как видим, под индексом частотной модуляции в радиопередающем устройстве понимается минимальное значение отношения девиации частоты к частоте модулирующего сигнала. В общем случае при ЧМ индекс модуляции изменяется в пределах

,

где F_МИН– минимальная рабочая частота модуляции.

Задание индекса модуляции в передатчиках и системах с ЧМ соотношением (*) является удобным (малое число), а главное – исчерпывающим, в чём мы убедимся при рассмотрении вопроса о занимаемой полосе частот ЧМ или ФМ колебанием.

В радиопередающих устройствах, особенно для целей радиовещания, предпочтение отдаётся ЧМ, а не ФМ. Это обусловлено следующими обстоятельствами.

1. Чтобы ЧМ и ФМ имели преимущества перед АМ в отношении помехоустойчивости, необходимо иметь индекс частотной или фазовой модуляции . Осуществить ФМ с большим индексом модуляции, как ниже будет показано, технически трудно, тогда как получить большой индекс ЧМ не столь сложно.

2. Частотный детектор проще фазового, следовательно, при использовании ЧМ для радиовещания упрощается приёмник, что важно с точки зрения его эксплуатации и стоимости.

Частотный спектр и занимаемая полоса частот ЧМ и ФМ колебаниями

Обратимся к выражению (29.13), описывающему ЧМ или ФМ колебание при модуляции гармоническим сигналом:

.

Воспользовавшись разложением косинуса двух углов в круглых скобках последнего выражения, можно представить его в следующей записи:

. (29.14)

Как видим, ЧМ или ФМ колебание можно разложить на два колебания с частотой , сдвинутых между собою по фазе на 90⁰(одно колебание изменяется по закону косинуса, а второе по закону синуса одного и того же аргумента, изменяющегося со временем пропорционально частоте). Амплитуды этих колебаний являются периодическими функциями времени следующего вида:

(**)

и

. (***)

Каждую из этих функций можно разложить в ряд Фурье.

Прежде, чем это сделать, рассмотрим случай, когда индекс модуляции мал и можно считать

а

.

В этом случае выражение (29.14) может быть представлено в следующем виде:

(29.15)

Согласно (29.15), ЧМ и ФМ колебания при малом индексе модуляции могут быть представлены, как и АМ колебание (24.5), в виде трёх гармонических составляющих. Первое слагаемое в (29.15) соответствует высокочастотному колебанию при отсутствии модуляции, то есть оно определяет колебание несущей частоты. Два других слагаемых обязаны модуляции и определяют колебания боковых частот: верхней и нижней. По сравнению с АМ колебанием (24.5) колебание нижней боковой частоты при ЧМ и ФМ оказывается сдвинутым по фазе на 180⁰относительно колебания нижней боковой частоты при АМ.²На рис.29.2,апредставлена векторная диаграмма, соответствующая выражению (29.15) для ЧМ и ФМ колебаний. Для сравнения на рис.29.2,бпредставлена векторная диаграмма АМ колебания.

При АМ вектор результирующего колебания изменяется по амплитуде. При ЧМ и ФМ вектор результирующего колебания совершает угловые колебания относительно положения вектора несущего колебания в пределах угла. Амплитуда результирующего колебания остаётся неизменной (согласно рис.29.2,авеличина вектора результирующего колебания при модуляции несколько превышает величину (амплитуду) несущего колебания, что обусловлено приближённостью представления ЧМ или ФМ колебания в виде трёх колебаний (29.15)).

В общем случае ЧМ и ФМ колебания могут быть представлены в виде суммы бесконечного числа гармонических колебаний с частотами , гдеn= 0, 1, 2, 3, …, амплитуды которых связаны с амплитудой немодулированного колебания функциями Бесселя первого родаn-го порядка с индексомв качестве аргумента. К такому выводу можно прийти, раскладывая в ряд Фурье функции (**) и (***).

Функция (**), будучи чётной функцией времени, при разложении в ряд Фурье содержит лишь косинусоидальные гармоники, причём лишь гармоники чётного порядка. Функция (***), как нечётная функция времени, при разложении в ряд Фурье содержит лишь синусоидальные гармоники, причём лишь нечётного порядка. В соответствии со сказанным можно записать:

.

Коэффициенты являются функциями Бесселя первого рода соответствующего порядка от аргумента.

Подставляя приведенные разложения функций (**), (***) в выражение (29.14), получаем (для сокращения записи начальную фазу высокочастотного колебания примем равной нулю ):

Воспользовавшись формулами

получаем:

(25.16)

Значения функций Бесселя разных порядков представлены в соответствующих книгах в виде таблиц и графиков в зависимости от аргумента. С помощью функций Бесселя можно вычислить амплитуды составляющих ЧМ или ФМ колебания.

Из разложения (25.16) следует, что ЧМ или ФМ колебание с несущей частотой , модулированное гармоническим сигналом с частотой, состоит из несущего колебания и бесконечного множества боковых компонент с частотами

.

При ЧМ и ФМ амплитуда несущего колебания и амплитуды боковых компонент являются функциями от индекса модуляции . Их значения изменяются при передаче одновременно с, то есть с амплитудой модулирующего сигнала при ЧМ и ФМ и дополнительно с частотой модуляции при ЧМ. Функции Бесселя имеют колебательный характер в зависимости от. Соответственно амплитуда несущего колебания и амплитуды боковых компонент имеют то же колебательное изменение, что и функции Бесселя, которым они пропорциональны, и проходят при этом через ряд нулевых значений. Например, амплитуда колебания с несущей частотой проходит через нуль при значениях

Отсюда следует, что составляющая спектра с частотой в модулированном колебании может отсутствовать. По этой причине частотупринято называтьсреднейилицентральной частотой ЧМ или ФМ сигнала, а не несущей, как её называют в спектре АМ колебания.

При небольших значениях индекса модуляции боковые компоненты порядка большего единицы имеют весьма малые значения по сравнению с боковыми компонентами первого порядка, а амплитуда колебания с несущей частотой изменяется очень незначительно относительно её немодулированного значения. Так при индексе модуляции амплитуда компоненты второго порядка не превышает 2% от амплитуды несущего колебания и 10% от амплитуды колебания первой боковой компоненты.

Если при малых индексах модуляции пренебречь компонентами выше первой, то выражение ЧМ и ФМ колебания (29.16) упрощается и принимает вид

, (29.17)

соответствующий (29.15).

Из сравнения (29.15) и (29.17) можно заключить, что при индексе модуляции значение функции Бесселя нулевого порядка, а значение функции Бесселя первого порядка.

Если обратиться к графикам функций Бесселя, то можно наглядно увидеть, что максимальное значение имеет функция, порядок которой примерно на единицу меньше аргумента. Это означает, что в спектре ЧМ или ФМ колебания наибольшую амплитуду имеет компонента, номер которой примерно на единицу меньше индекса модуляции . Соответственно на долю этой компоненты приходится и большая часть мощности модулированного колебания. Вообще приосновная часть мощности ЧМ или ФМ колебания приходится на долю боковых частот, которые обязаны модуляции и, следовательно, несут информацию. Этим и объясняются более высокая помехоустойчивость и хорошие энергетические показатели при ЧМ и ФМ.

Чем больше индекс модуляции, тем дальше от средней частоты колебания располагаются на оси частот боковые колебания с максимальной амплитудой. Амплитуды компонент ЧМ и ФМ колебания, номер которых больше индекса модуляции, оказываются незначительными и уровень их резко убывает с возрастанием номера компоненты. Это обстоятельство позволяет ограничить рабочую полосу частот, занимаемую ЧМ или ФМ колебанием.

Если ограничить спектр ЧМ или ФМ колебания на уровне компоненты с амплитудою 1% от амплитуды немодулированного колебания, то с достаточной точностью полосу частот ЧМ или ФМ колебания можно определить по формуле

. (29.18)

При ФМ индекс модуляции не зависит от частоты модуляции, а при ЧМ – зависит и определяется соотношением

.

Соответственно для ЧМ колебания формулу (29.18) можно записать в виде

. (29.19)

Из (29.18), (29.19) следует, что при модуляции сложным сигналом рабочую полосу частот ЧМ и ФМ колебаний следует определять, исходя из максимальной частоты модуляции F_МАКС. Определённая при этом полоса частот заведомо окажется шире устанавливаемой формулами (29.18) и (29.19) для меньших частот модуляции. Следовательно, если высокочастотный тракт передатчика или системы с ЧМ или ФМ будет рассчитан на полосу частот при максимальной частоте модуляции, то при работе с меньшими частотами модуляции полоса частот высокочастотного тракта будет более чем достаточной. В этом также причина указания индекса модуляции при ЧМ соотношением (*)

.

Следует отметить, что определение полосы частот ЧМ и ФМ колебания по формулам (29.18), (29.19) дано на энергетической основе: в этой полосе сосредотачивается практически вся энергия колебания. За пределами этой полосы оказываются компоненты, амплитуда каждой из которых не превышает 1% от амплитуды немодулированного колебания. В реальности систему передачи необходимо рассчитывать на основании условия, чтобы внесённые искажения не превышали определённые, заранее заданные пределы.

Если принять, чтобы за пределами полосы оказывались компоненты, амплитуды которых не превышают 5% от немодулированного колебания, то рабочая полоса частот ЧМ или ФМ колебания определяется соотношением

. (29.20)

При ЧМ можно также считать

.

Искажения сигнала за счёт ограничения пропускаемого спектра ЧМ или ФМ колебания при выборе полосы высокочастотного тракта согласно (29.20) не превышают единиц процентов.

Согласно (29.20) полоса частот, занимаемая ЧМ или ФМ колебанием, оказывается в раз шире полосы частот АМ колебания. Приполосы частот ЧМ, ФМ и АМ колебаний практически одинаковы. Приполоса частот ЧМ колебания.

Ограничение спектра ЧМ или ФМ колебания высокочастотным трактом обусловливает появление у сигнала на выходе тракта амплитудной модуляции. Очевидно, чем с более высоким уровнем будут ограничены компоненты, тем больше будет глубина возникающей АМ.³Для уменьшения глубины возникающей АМ следующий каскад ставится в перенапряжённый режим или сигнал подвергается амплитудному ограничению.⁴

Ранее мы отмечали, чтобы передача с использованием ЧМ или ФМ имела преимущества перед АМ в отношении помехоустойчивости, необходимо иметь . А это приводит к существенному расширению рабочего спектра ЧМ или ФМ колебания и занимаемой им полосы частот (29.18), (29.20). Поэтому ЧМ применяется в передатчиках с рабочей частотой более (30…40) МГц, то есть начиная с метрового диапазона волн.

Так как линия радиосвязи с ЧМ более помехоустойчива, чем с АМ, то на таких линиях можно работать с менее мощными передатчиками. Сами передатчики с ЧМ имеют ряд преимуществ перед передатчиками с АМ:

1. Во-первых, более полно используется мощность генераторного прибора выходного каскада передатчика. При этом мощность передатчика одинакова как при отсутствии, так и при наличии модулирующего сигнала, так как амплитуда сигнала с ЧМ неизменна.

2. Во-вторых, промышленный КПД передатчика с ЧМ в 1,3…1,5 раза выше, чем передатчика с АМ, так как выходной каскад работает в наиболее выгодном режиме: обычно критическом или слабо перенапряжённом. Также мощность, потребляемая частотным модулятором, значительно ниже мощности, потребляемой амплитудным модулятором.

3. В-третьих, при ЧМ легче получить линейность модуляции.

К основным характеристикам, определяющим работу ЧМ передатчика, относятся:

1. Статическая модуляционная характеристика, представляющая зависимость изменения частоты передатчика от постоянного напряжения на входе частотного модулятора:.

2. Динамическая модуляционная характеристика – зависимость девиации частоты или индекса модуляцииот амплитуды модулирующего сигнала при неизменной частоте модуляции:

3. Амплитудно-частотная характеристика

где F– частота модулирующего сигнала.

Осуществление фазовой модуляции (ФМ)

Основным методом осуществления ФМ является подключение к резонансному контуру в выходной цепи АЭ усилительного каскада управляемой реактивности, величина которой изменяется пропорционально амплитуде модулирующего сигнала.

В качестве управляемой реактивности в настоящее время наиболее часто используется барьерная ёмкость p-n-перехода полупроводникового диода. Для этой цели существуют специальные диоды, называемыеварикапами(см. лекцию 18). На рис.29.3 представлена схема, поясняющая принцип осуществления ФМ с использованием варикапа.

Контур образован индуктивностьюLи ёмкостью варикапаС_В. С помощью делителя напряжения коллекторного питания на диод с резистораR₂подаётся обратное напряжение на варикап, обусловливающее рабочую точку при отсутствии модулирующего сигнала. При этом контур настроен на частоту входного сигналаω₀. Под воздействием модулирующего сигнала изменяется ёмкость варикапа, соответственно изменяется резонансная частота контураω_Котносительно средней частотыω₀.

Пусть на входе транзистора действует сигнал . Обусловленная этим сигналом амплитуда первой гармоники коллекторного тока. Комплексная амплитуда колебательного напряжения на контуре

, (29.21)

где – комплексное сопротивление контура на центральной частоте, определяемое расстройкой относительно средней частотыω₀.

ФЧХ контура (рис.29.4)

, (29.22)

где Q– добротность контура.

В пределах значений ±0,5 радиана (примерно ±30⁰) ФЧХ контура оказывается практически линейной. Соответственно, максимальное изменение фазы, определяющее девиацию начальной фазы при ФМ, которое может быть получено в рассматриваемой схеме при обеспечении линейной модуляции, не превышает 0,5 радиана. Напомним, что при ФМ девиация начальной фазы колебания и индекс модуляции являются одним и тем же параметром.

При небольших расстройках контура выражение (29.22) может быть записано в виде

.

Если учесть, что относительное изменение резонансной частоты контура связано с изменением ёмкости и индуктивности контура соотношением (см. лекцию 22)

,

то при изменении ёмкости контура фазовый угол его сопротивления на средней частоте можно считать равным⁵

.

Согласно последнему выражению положительное приращение ёмкости контура, приводящее к понижению резонансной частоты контура относительно средней частоты, обусловливает изменение фазового угла в области отрицательных значений, а отрицательное приращение ёмкости контура, приводящее к повышению резонансной частоты контура, обусловливает изменение фазового угла в области положительных значений.

Для мгновенного напряжения на выходе усилителя (рис.29.3), учитывая (29.21), можно записать

,

где начальная фаза колебания изменяется под воздействием модулирующего сигнала.

Так как при расстройке контура изменяется модуль его сопротивления , то, очевидно, фазовая модуляция в рассматриваемой схеме сопровождается паразитной амплитудной модуляцией. Чем больше пределы изменения фазового угла, тем больше паразитная АМ.

Большая девиация начальной фазы колебания и меньшая паразитная АМ могут быть получены при использовании в выходной цепи АЭ усилительного каскада многоконтурных цепей, в частности, трёхконтурной колебательной системы, каждый из контуров которой перестраивается с помощью варикапа. Схема усилителя с колебательной системой из трёх одинаковых контуров, перестраиваемых варикапами, представлена на рис.29.5.

В схеме (рис.29.5) может быть обеспечена девиация фазы до ±40⁰на каждый контур при нелинейных искажениях, не превышающих 2%, и практически отсутствующей АМ. Если допустить несколько большие нелинейные искажения, то в последней схеме может быть достигнута девиация фазы до ±180⁰.

Усилители по схемам рис.29.3 и рис.29.5, а также им подобные устройства, используемые для осуществления ФМ, принято называть фазовыми модуляторами.

В последнее время в связной аппаратуре часто применяют фазовые модуляторы в виде простых RLC-фазовращателей, в которых в качестве управляемого сопротивления используется полевой транзистор. Схема такого фазового модулятора представлена на рис.29.6.

Если выбрать ёмкость цепи (рис.29.6)

то коэффициент передачи этой цепи по напряжению на частоте входного высокочастотного сигнала

. (29.23)

Как видно из (29.23), при любом значении Rмодуль коэффициента передачи по напряжению рассматриваемой цепи на частоте высокочастотного сигналаK= 1. Соответственно паразитной АМ нет. Сдвиг по фазе между входным и выходным высокочастотными сигналами, как следует из (29.23),

. (29.24)

Согласно (29.24), если сопротивление Rизменять от 0 до ∞ , то фаза будет изменяться от 0 до 180⁰. Очевидно, в реальной цепи не может быть обеспечено как нулевое, так и бесконечное значение сопротивленияR. Кроме того, если даже допустить такое изменение сопротивления, то характер изменения фазы (29.24) будет весьма нелинейным, что неприемлемо для целей ФМ. При изменении сопротивленияRв пределахR_МИН…R_МАКСфаза выходного сигнала (29.24) изменяется в пределах. При этом девиация фазы при осуществлении ФМ будет равна половине интервала изменения фазы, то есть

. (29.25)

При модуляции гармоническим сигналом сопротивление Rизменяется по закону

,

где – коэффициент модуляции сопротивления резистора;R_СР– значение сопротивления резистора в режиме несущей частоты, то есть при отсутствии модулирующего сигнала.

Если установить при отсутствии модулирующего сигнала , то, согласно (29.24), для этого необходимо обеспечить

.

Максимальное значение фазы согласно (29.24)

,

минимальное значение фазы

.

Девиация фазы (29.25) .⁶Например, приm_R= 0,6 получаем, то есть примерно 28,5⁰. Исследования показывают, что при рассмотренном выборе параметров фазовращателя (рис.29.6) имеют место заметные нелинейные искажения ФМ.

На рис.29.7 приведена схема активного мостового фазового модулятора, применяемого в радиостанциях подвижной связи.

ЭлементыR1,R2,R,C_В,Lпо структуре формируют цепь, подобную классической мостовой схеме (см. рис.16.3, лекция 16), но эта цепь не является сбалансированным мостом. На нагрузкахR1,R2 в коллекторной и эмиттерной цепях транзистора формируются два одинаковых по амплитуде, но противофазных напряжения, которые прикладываются к ветвям мостаR,C_В,L. В схеме обеспечивается девиация начальной фазы колебания до 50…60⁰при хорошей линейности и малой паразитной АМ.

В заключение отметим, что, очевидно, в качестве фазового модулятора может быть использован практически любой электрически управляемый фазовращатель соответствующего диапазона частот.⁷

Осуществление частотной модуляции (ЧМ)

Частотная модуляция (ЧМ) связана с изменением частоты высокочастотного колебания под воздействием управляющего сигнала. Так как частота колебаний определяется автогенератором, то, очевидно, ЧМ возможна в автогенераторе. С другой стороны, частотная и фазовая модуляции (ЧМ и ФМ) тесно связаны между собою, что дало основание объединить их в один вид угловоймодуляции. Тесное родство ЧМ и ФМ позволяет осуществлять один вид модуляции, а результат на выходе иметь соответствующим другому виду модуляции. Например, можно осуществлять ФМ с использованием любой из рассмотренных выше схем, а выходное колебание получать при этом со свойствами ЧМ колебания. Очевидно, можно и наоборот: осуществлять ЧМ, а результирующее колебание получать со свойствами ФМ колебания. То есть возможно преобразование колебания одного вида (модуляции) в колебание другого вида (модуляции).⁸Для преобразования ФМ в ЧМ и наоборот модуляция должна осуществляться сигналом, отличным от оригинального (исходного). В частности, если осуществить ФМ сигналом, полученным путём интегрирования исходного модулирующего сигнала, то характеристики полученного колебания относительно исходного модулирующего сигнала будут как у ЧМ колебания. Действительно, пусть исходный модулирующий сигнал как и прежде

.

После интегрирования он принимает вид

,

где C₀– постоянная интегрирования.

При осуществлении ФМ проинтегрированным сигналом получаем

. (29.10^/)

Постоянная интегрирования С₀вошла в значение.

. (29.11^/)

. (29.12^/)

Частота результирующего колебания

.

Как видим, девиация частоты результирующего колебания не зависит от частоты модуляции, а прямо пропорциональна амплитуде модулирующего сигнала, что характерно для ЧМ колебания. Таким образом результатом фазовой модуляции проинтегрированным сигналом стало колебание с частотной модуляцией.

Из сказанного выше следует, что возможны два основных метода осуществления ЧМ:

первый – путём непосредственного изменения частоты автогенератора, называемыйпрямымметодом ЧМ. Структурная схема прямого метода ЧМ показана на рис.29.8.

второй – с помощью фазовых модуляторов или метод получения частотной модуляции из фазовой, называемый такжекосвеннымметодом ЧМ. Одна из возможных структурных схем этого метода представлена на рис.29.9.

При чисто фазовой модуляции в схеме (рис.29.9) отсутствует интегрирующая цепь.

Остановимся подробнее на рассмотрении этих двух методов осуществления ЧМ.

При первом методе параллельно контуру или последовательно в контур автогенератора (АГ) подключается управляемая реактивность (частотный модулятор), с помощью которой осуществляется изменение частоты автоколебаний. Напомним, что в случае, например, одноконтурного АГ изменение частоты автоколебаний, практически определяемой резонансной частотой контура АГ, связано с изменением реактивностей контура L_К,С_Ксоотношением (см. (22.1), лекция 22)

.

Под воздействием модулирующего сигнала изменяется один или оба реактивных параметра контура АГ относительного среднего значения при отсутствии модуляции. Согласно последнему соотношению получаемая при этом девиация частоты АГ

.

Если в последующих каскадах осуществляется умножение частоты в nраз, то соответственно увеличивается и девиация частоты на выходе (средняя частота автоколебаний также возрастает вnраз), то есть

.

Очевидно, ЧМ легче осуществить в АГ с параметрической стабилизацией частоты, имеющем относительно невысокую стабильность её (см. лекцию 22). При этом нестабильность частоты возрастает за счёт подключения к контуру АГ одной или двух управляемых реактивностей частотного модулятора.⁹Отсюда следует, что один из наиболее сложных вопросов, возникающих при первом методе ЧМ, заключается в стабилизации средней частоты колебаний АГ и передатчика в целом.

Для стабилизации средней частоты рабочих колебаний при прямом методе осуществления ЧМ могут быть использованы системы АПЧ: частотная или фазовая (см. лекцию 23). Одна из возможных структурных схем с использованием системы частотной автоподстройки (ЧАП) средней частоты ЧМ автогенератора представлена на рис.29.10.

Обозначения на схеме: УПЧ – усилитель промежуточной частоты; ЧД – частотный детектор; ФНЧ – фильтр нижних частот.

При таком способе стабилизации средней частоты автогенератор работает обычно или непосредственно на рабочей частоте передатчикаf₀=f_ПЕРЕД, или на частотеf₀в (2 – 3) раза меньше частоты передатчикаf_ПЕРЕД, что значительно упрощает схему и конструкцию передатчика. Необходимо так выбрать параметры системы АПЧ, чтобы она реагировала на относительно медленные изменения частоты стабилизируемого генератора, вызванные действием дестабилизирующих факторов, и не реагировала на более быстрые отклонения частоты, вызванные действием модулирующего сигнала. Для этого необходимо, чтобы частота среза ФНЧF_СРбыла ниже низшей частоты модуляцииF_МИН(рис.29.11, гдеk_ФНЧ– коэффициент передачи ФНЧ).

Стабилизация средней частоты может быть произведена с помощью интерполяционной схемы (рис.29.12).

Вэтом случае частота выходного колебанияf=f₀образуется в результате сложения частоты колебаний опорного (кварцевого) АГf_КВи частоты АГ с параметрической стабилизацией частотыf_АГ, в котором осуществляется частотная модуляция с девиацией частоты. Если выполняется соотношениеf_КВ>>f_АГ, то нестабильность частоты выходных колебаний, соответственно и нестабильность средней частоты получаемого ЧМ колебания, практически определяется нестабильностью частоты опорного генератора с кварцевой стабилизацией частоты.

При рассмотрении кварцевых АГ было отмечено (см. лекцию 22), что в осцилляторных схемах частота автоколебаний может изменяться в некотором интервале между частотами последовательного и параллельного резонансов кварцевого резонатора. Это обстоятельство позволяет осуществлять в небольших пределах ЧМ в кварцевом АГ путём подключения параллельно кварцевому резонатору или последовательно с ним управляемой ёмкости, например, варикапа. Изменение частоты КАГ может быть получено в пределах (0,01…0,08)% собственной частоты кварцевого резонатора. Практически в осцилляторных схемах КАГ при частоте порядка 10 МГц получают девиацию частоты до 1 кГц. При ЧМ КАГ никаких специальных мер для стабилизации средней частоты колебаний не требуется. ЧМ в КАГ находит применение в основном в радиопередающих устройствах низовой связи, так как при этом методе имеют место довольно значительные нелинейные искажения передаваемого сигнала в дополнение к несколько пониженной стабильности средней частоты рабочих колебаний и невозможности получения большой девиации частоты.

Для большинства линий радиосвязи с ЧМ величина нестабильности средней частоты передатчика выбирается из соотношения . При широкополосной ЧМ, соответственно при большой девиации частоты, это условие можно выполнить без применения специальных мер по стабилизации средней частоты.

При втором – косвенном методе ЧМ, когда ЧМ колебание получается путём осуществления ФМ проинтегрированным сигналом модуляции, получаемая девиация начальной фазы, как следует из (29.10^/),

оказывается зависящей от частоты модуляции, а не только от амплитуды модулирующего сигнала. При одинаковой амплитуде модулирующего сигнала, как видим, максимальное значение девиации начальной фазы колебания получается на нижней частоте модуляции. Так как в каждой схеме осуществления ФМ девиация начальной фазы колебания не может быть получена больше некоторого значения , например, больше 0,5 радиана в схеме рис.29.3, то это значение при косвенном методе ЧМ может быть допущено только на нижней частоте модуляции. Соответственно получаемая при этом методе девиация частоты

. (29.26)

Если принять, например, , а нижнюю частоту модуляцииF_МИН= 100 Гц, то получаемая девиация частоты составит всего 50 Гц. В системах ЧМ вещания и звукового сопровождения телевидения необходимая девиация частоты устанавливается ±50 кГц или ±75 кГц. Для получения столь большой девиации частоты необходимо осуществить умножение получаемой девиации частоты в 1000 или в 1500 раз, что потребует применения большого числа умножителей частоты. Напомним, что с умножением девиации частоты умножается и средняя частота колебания. Необходимость многократного умножения девиации частоты и связанное с этим умножение средней частоты колебания существенно усложняют построение передатчика. Но при этом методе ЧМ не требуется применять какие-либо меры по стабилизации средней частоты, так как в качестве источника исходного модулируемого колебания используется автогенератор с кварцевой стабилизацией частоты.

Если обозначить необходимую девиацию частоты выходного колебания (в случае передатчика это девиация частоты передатчика) , то, учитывая (29.26), для получения такой девиации частоты необходимо осуществить умножение частоты исходного модулируемого колебания вnраз:

. (29.27)

Зная необходимую частоту выходного колебания (рабочую частоту передатчика) , можно определить частоту исходного модулируемого колебания

. (29.28)

Частота исходного модулируемого колебания f_АГдолжна быть достаточно высокой (минимум в 5…10 выше максимальной частоты модуляцииF_МАКС), чтобы не возникали большие нелинейные искажения при модуляции. Таким образом, если даваемое (29.28) значение частоты превышает (5…10)F_МАКС, то частота исходного кварцевого АГ выбирается согласно (29.28) и в последующих каскадах осуществляется умножение частоты вnраз. Структурная схема реализации метода в этом случае совпадает со схемой рис.29.9. Если даваемое (29.28) значение частоты оказывается ниже допустимого, то выбирается частота исходного колебания, превышающая максимальную частоту модуляцииF_МАКСв необходимое число раз. Очевидно, если осуществить в последующих каскадах умножение частоты вnраз, то у выходного колебания девиация частоты будет равна заданной, а средняя частота выходного колебания окажется выше необходимой (например, рабочей частоты передатчика). В этом случае потребуется произвести понижение (гетеродинирование) частоты полученного колебания до нужного значения. Девиация частоты при этом сохранится без изменения. Если потребуется производить понижение частоты полученного колебания, то обычно это делается на промежуточном этапе. В этом случае выбирается частота исходного колебанияf_АГи осуществляется модуляция с девиацией частоты, определяемой (29.26). Полученное колебание подвергается умножению частоты вn₁раз. После умножения получаем колебание со средней частотойn₁f_АГи девиацией частоты. Используя гетеродин (высокостабильный АГ) с частотойf, с помощью смесителя (как в интерполяционной схеме) выделяем колебание разностной частоты, например,

f–n₁f_АГ,

имеющее девиацию частоты .

Полученное колебание подвергается умножению частоты в n₂раз. Средняя частота получаемого колебания должна быть равна требуемой частоте выходного колебания (рабочей частоте передатчика), то есть должно иметь место

.

Девиация частоты выходного колебания должна быть равна требуемой, то есть должно быть

.

Из сравнения последнего соотношения с (29.27) следует, что должно быть n₁n₂=n. Необходимая частота гетеродина.

Структурная схема реализации косвенного метода ЧМ в этом случае представлена на рис.29.13.

В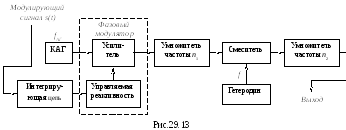качестве интегрирующей цепи обычно используется цепочка ФНЧRC– типа, представленная на рис.29.14.

Напряжение на выходе такой цепочки

.

При , где– низшая модулирующая частота, амплитуда выходного напряжения

оказывается обратно пропорциональной частоте и прямо пропорциональной амплитуде модулирующего сигнала.¹⁰Если таким сигналом осуществить ФМ, то результатом будет колебание со свойствами ЧМ.

При указанных параметрах элементов цепи (рис.29.14) изменение частоты сигнала в два раза приводит к изменению амплитуды выходного напряжения также в два раза. Соответственно, крутизна АЧХ рассматриваемого фильтра составляет – 6 дБ на октаву.

Следует отметить, что в силу определённой громоздкости косвенный метод ЧМ в современных разработках радиовещательных и телевизионных передатчиков почти не используется. В то же время он практикуется в радиопередатчиках низовой связи с использованием фазовых модуляторов по схемам (рис.29.3 и рис.29.5 – рис.29.7).