Основы радиосхемотехники / Учебник по САЭУ(2005) / САЭУ кн.2 / Приложение 5-укороченное

134

Приложение 5

Дискретизация аналоговых сигналов

В третьем разделе восьмой главы показано, что при обработке аналоговых сигналов в дискретно-аналоговых устройствах с коммутируемыми цепями происходят специфические искажения, которые возрастают с уменьшением частоты переключения.

В связи с этим возникают вопросы, связанные с возможностью потери информации (или сведения этих потерь к минимуму), при переходе от аналоговых сигналов к дискретно-аналоговым, в частности в устройствах с переключаемыми конденсаторами. Ответы на эти вопросы можно получить из известных работ Найквиста и Котельникова. Кратко изложим постановку задачи и основной результат их исследований, пользуясь частотными представлениями сигналов. Необходимо было определить: можно ли точно восстановить аналоговый сигнал S(t) или его спектральную интенсивность S(jωt), располагая значениями сигнала только в дискретные моменты времени t_k=Δtk, и какой должен быть при этом интервал дискретизации Δt? Для решения задачи рассмотрим функциональную схему устройства, проводящего дискретизацию аналогового сигнала, которая изображена на рис.П.5.1.

Устройство дискретизации представляет собой умножитель сигналов, на первый вход которого поступает аналоговый сигнал S(t), а на второй- сигнал функции дискретизации S_Д(t). Положим, что функция S_Д(t) является периодической и отлична от нуля только в моменты времени t=Δt n. Предположим также, что в указанные моменты её значения равны бесконечности, тогда S_Д(t) запишется в виде:

(П.5.1)

.

. Можно было бы записать сигнал S_Д(t) в виде суммы бесконечного числа коротких прямоугольных импульсов сдвинутых на одинаковые временные интервалы Δt и с постоянной амплитудой. При этом дальнейшие математические выкладки оказались бы более громоздкими. Однако основной результат исследования при таком предположении будет практически таким же, как и при записи функции S_Д(t) в виде (П.5.1)

Периодическая функция S_Д (t) может быть разложена в ряд Фурье, её период равен интервалу дискретизации Δt:

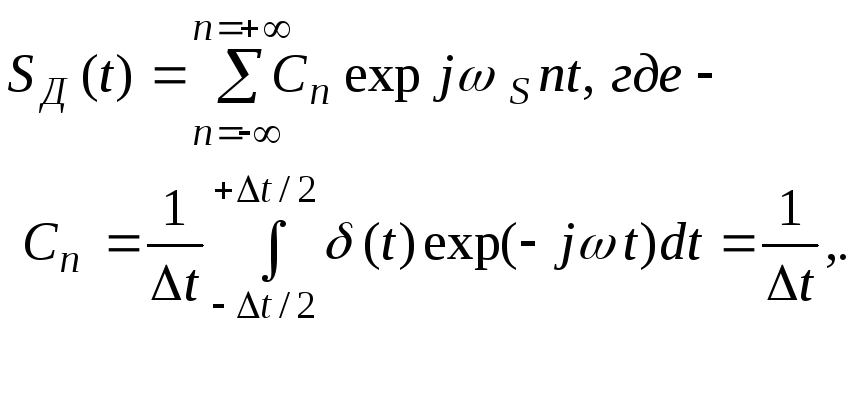
ω_S- угловая частота дискретизации ω_S=2π/Δt. Следовательно:

Определим спектральную интенсивность S_Д(jω) сигнала S_Д(t):

=

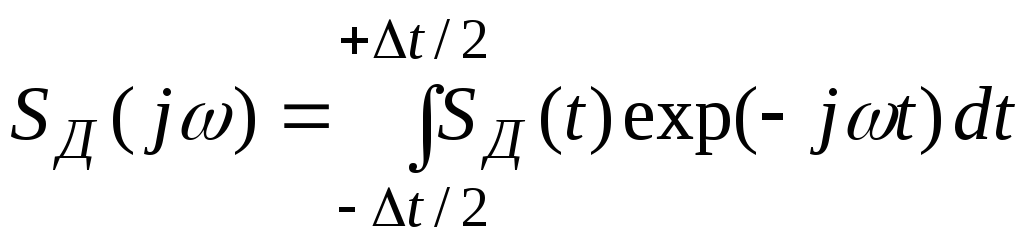(П.5.2)

Таким образом, спектральная интенсивность S_Д(jω) функции S_Д(t) равна сумме дискретных частот кратных частоте дискретизации . Чтобы определить спектральную интенсивность выходного сигнала S_ВЫХ(t), воспользуемся теоремой для определения спектра произведения двух функций (теоремой свертки в частотной области). Положим, что нам известна спектральная интенсивность входного сигнала S(t):

.

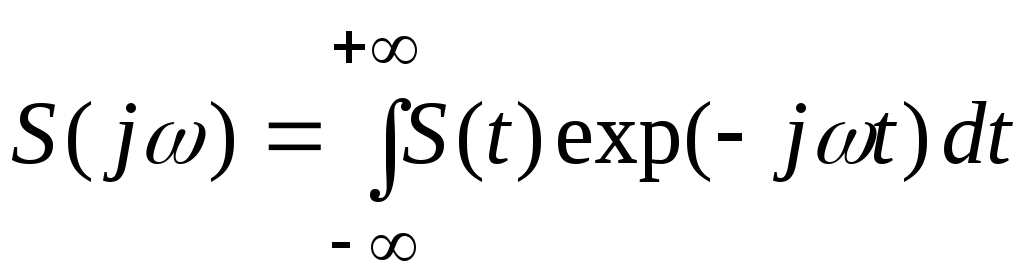Определим спектральную интенсивность сигнала S_ВЫХ(t) на выходе устройства, изображенного на рисункеП.5.1. Используя теорему о свертке, запишем:

.

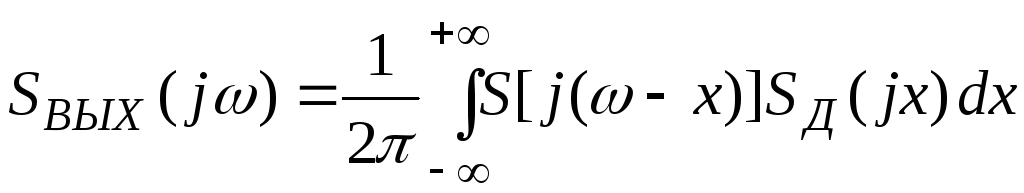Подставляя в последнее выражение спектральные интенсивности входного сигнала S(jω) и сигнала S_Д(t), а также используя фильтрующее свойство дельта-функции, получим:

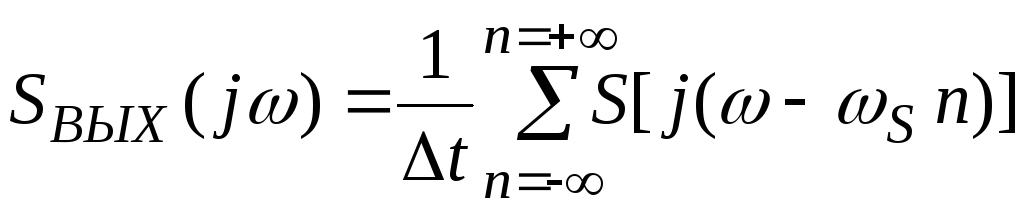(П.5.3)

Выражение (П.5.3)указывает, что спектр сигнала на выходе устройства равен спектру входного сигнала и бесконечной сумме его спектров, смещенных по оси частот на величину кратную частоте дискретизации ω_S.С физической стороны этот результат можно объяснить следующим образом. Поскольку спектральная интенсивность функции S_Д(t), помимо дельта-функции на частоте ω=0, содержит бесконечную сумму дискретных частот (дельта-функций) кратных ω_S , то после перемножения сигнала S_Д(t) с сигналом S(t),на выходе устройства кроме основного спектра S(jω) входного сигнала будут дополнительные слагаемые

,

т.е. смещенные по частоте на величину спектры входного сигнала. Число таких слагаемых бесконечно. На рис.П.5.2. приведены зависимости модуля спектральной интенсивности входного и выходного сигналов от частоты. На рисунке приведен пример, когда частичные спектры выходного сигнала перекрываются. В этом случае с помощью частотной фильтрации на выходе устройства невозможно восстановить исходный сигнал после его дискретизации. Однако все сигналы имеют практически ограниченный частотный диапазон. Введя в рассмотрение верхнюю частоту ω_S спектра входного сигнала и учитывая четность спектра, можно считать, что перекрытия спектров сигнала после его дискретизации не будет, если выполнено условие:

(П.5.4)

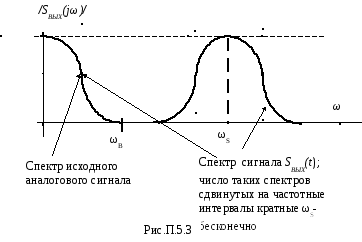
На рис.П.5.3 приведены спектры входного и выходного сигналов при выполнении условия (П.5.4) , при котором спектры не перекрываются. В этом случае имеется возможности восстановления сигнала после его дискретизации. Приведем формулировку теоремы отсчетов ( теоремы Найквиста-Котельникова):

Аналоговый сигнал можно практически восстановить без искажения, используя его дискретные отсчеты в моменты времени кратные Δt, если частота дискретизации ω_S будет превышать в два раза или более верхнюю частоту спектра ω_В исходного сигнала.

Применительно к фильтрам с переключаемыми конденсаторами, рассмотренными в разделе 8.3, условие теоремы Найквиста-Котельникова означает, что частота коммутации ПК должна удовлетворять условию (П.5.4) Таким образом, переключаемые конденсаторы в дискретно-аналоговых устройствах можно рассматривать с одной стороны как имитаторы резисторов больших номиналов, а с другой, как элементы аналоговой памяти обрабатываемых сигналов внутри интервалов дискретизации.

При рассмотрении вопросов дискретизации сигналов и их восстановления предполагалось наличие идеальной функции дискретизации S_Д(t) равной сумме бесконечного числа дельта-функций, которые сдвинуты на интервалы по оси времени на величину кратную Δt.В реальных устройствах функция S_Д(t) может быть выполнена в виде периодической последовательности прямоугольных импульсов конечной длительности Δt_К с ограниченной амплитудой А₀ .

/S_ВЫХ(jω)/

Исходный спектр Частичные спектры сигнала

аналогового сигнала S_ВЫХ(t) перекрываются

Рис. П.5.2

При этом обычно выполняется условие малости Δt_K по сравнению с Δt: Δt_К<< Δt. Вследствие этого разложение реальной периодической функции дискретизации не совпадает с разложением, которое соответствует выражению (П.5.2). Особенность разложения реальной функции дискретизации приводит к тому, что амплитуды дискретных составляющих оказываются не постоянными и равными бесконечности в моменты кратные Δt, а пропорционально уменьшаются с увеличением номера гармоник разложения в соответствии с законом изменения модуля функции Sin(nω_S)/(nω_S). Учет этого обстоятельства приводит к тому, что повторяющиеся по форме спектры сигнала на выходе устройства уменьшаются по величине с увеличением их частотного интервала nω_S относительно максимума частоты исходного спектра. Этот эффект равносилен уменьшению верхней частоты спектров составляющих nω_В, гарантируя усиленное выполнение теоремы Найквиста-Котельникова.

Для восстановления сигнала S(t) из S_ВЫХ(t) необходимо после его дискретизации провести частотную фильтрацию с помощью устройства, которое не пропускает частотные составляющие сигнала S_ВЫХ(t) кроме частот спектра исходного аналогового сигнала S(t). Если полагать, как это изображено на рис. П.5.1и П.5.3, что входной сигнал относится к видеосигналам, т.е. его спектр расположен в окрестности нулевой частоты, то для его выделения из сигнала S_ВЫХ(t) необходимо применить фильтр нижних частот с идеальной частотной характеристикой. Частота среза такого фильтра должна быть в точности равна ω_В .Требование идеальной АЧХ такого фильтра, которое практически невыполнимо, приводит к погрешности при восстановлении аналоговых сигналов, поступающих на вход дискретно-аналогового устройства, каким является в частности фильтр, использующий переключаемые конденсаторы.

При проектировании дискретно-аналоговых устройств используется математический аппарат Z-преобразования, который отличается от преобразования Лапласа. Ядром интегрального преобразования Лапласа является функция:

,

а дискретного Z-преобразования функция ,

где Δt- интервал дискретизации сигналов в дискретно-аналоговом устройстве.

Линейные устройства, к которым относятся и фильтры рассмотренные в гл.7, имеют операторный коэффициент передачи К(р) в виде дробно-рациональных функций комплексного переменного р. К сожалению Z-преобразование с ядром

или

переводит дробно-рациональную функцию К(р) в трансцендентную функцию К(Z), что затрудняет проектирование дискретно-аналоговых устройств и их расчет. Для исключения таких затруднений точное соотношение между комплексными переменнымиZ и р: заменяют различными приближениями. В частности используется разложение натурального логарифма в ряд:

, (П.5.5)

и учитывается только первый член разложения. В этом случае:

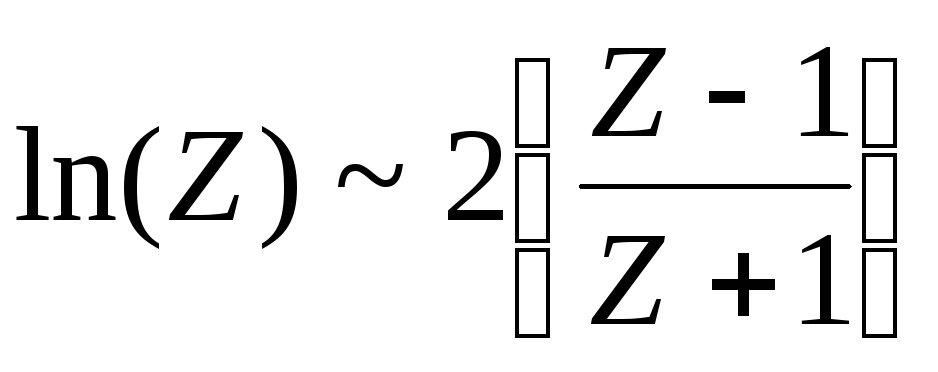(П.5.5^/)

Преобразование (П.5.5^/) называется билинейным. При этом

и .

В этом случае при билинейном преобразовании (П.5.5^/), как и при преобразовании Лапласа, комплексный коэффициент передачи дискретно-аналогового устройства записывается также в виде дробно-рациональной функции, как и у аналогового устройства. Но имеется некоторое различие в поведении этих коэффициентов передачи. При преобразовании Лапласа и изменении частоты аналогового фильтра от нуля до бесконечности функция ядра движется в области комплексного переменного по окружности единичного радиуса с периодическим повторением в фазовом интервале: 0<t<2π . При преобразовании (П.5.5^/) и изменении частоты дискретно-аналогового устройства в тех же пределах функция ядра Z-преобразования движется в комплексной плоскости по окружности единичного радиуса с тем же с периодическим её повторением в фазовом интервале 0< Δt<2π, но с другим значением частоты.

Вследствие этого частота аналогового устройстване совпадает с частотой дискретно-аналогового. Можно показать[12], что между этими частотами существует нелинейная зависимость, которая определяется соотношением:

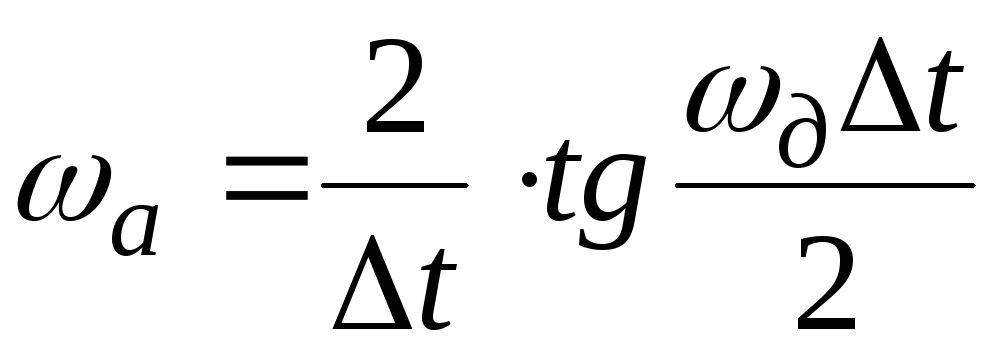, (П.5.6)

или

(П.5.6^/)

Согласно (П.5.6^/) при частота дискретно-аналогового устройства достигает только конечного предельного значения равного . При высокой частоте дискретизации, когда Δt мало ( частота дискретизации примерно в восемь раз превышает верхнюю частоту спектра сигнала), функцию тангенса в выражении (П.5.6) приближенно можно заменить линейной:

.

тогда .

Следовательно, если частота дискретизации достаточно высокая, что означает отсутствие перекрытия спектров в сигнале S_ВЫХ(t), то изменения масштаба частот и при переходе от аналогового устройства к дискретно-аналоговому не происходит.