2.3.2. Силовой расчет группы звеньев 4 и 5

Выделим из механизма группу звеньев 4 и 5 в масштабе (рис. 2.6). В характерных точках расставим силы и моменты сил, действующие на звенья структурной группы. Действие на рассматриваемую группу отброшенных звеньев заменяем реакциями. В индексе обозначения реакций ставятся две цифры: первая показывает, со стороны какого звена действует сила, а вторая – на какое звено действует сила.

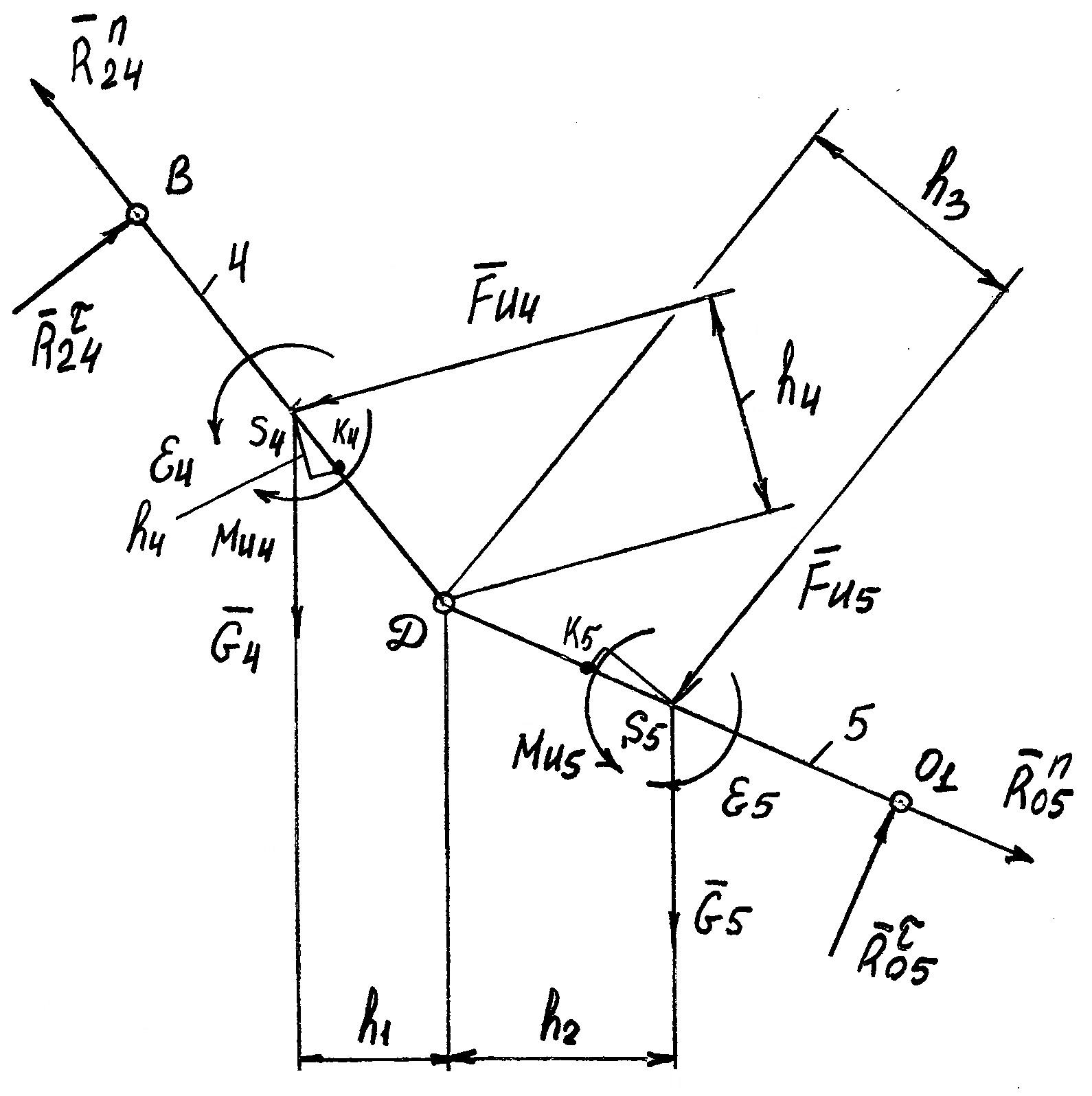
Рис. 2.6. Группа из 4 и 5 звеньев механизма, μ_l = 0,008 м/мм

Определим реакцию из уравнения

.

.

Величины , , , изображенные в масштабе , сняты с чертежа в мм, поэтому необходимо делить на масштаб .

Определим реакцию из уравнения

.

.

Определим реакции , , , из векторного уравнения , .

Строим план сил для группы звеньев 4 и 5 в масштабе

(рис. 2.7).

Рис. 2.7. План сил для группы звеньев 4 и 5, μ_F = 4,48 Н/мм

Тогда вектора-отрезки сил на плане сил будут:

;

;

;

;

;

.

Из плана сил

;

;

.

Определим реакцию из векторного уравнения , .

Из плана сил – на чертеже показана пунктиром.

2.3.3. Силовой расчет группы звеньев 2 и 3

Выделим из механизма группу звеньев 2,3 и расставим все нагрузки: силы тяжести; силы инерции и моменты сил инерции; реакции со стороны отброшенных звеньев. В точке B действует реакция со стороны отброшенного четвертого звена на второе. равна и направлена противоположно (рис. 2.8).

Рис. 2.8. Группа звеньев 2 и 3, μ_l=0,008 м/мм

Определим реакцию из уравнения :

.

;

.

Определим реакции , , из векторного уравнения :

.

Зная силы, выберем масштаб сил и вычислим соответствующие им длины отрезков:

Строим план сил для группы звеньев 2 и 3 (рис. 2.9). Из плана сил определим , , :

;

;

.

Рис. 2.9. План сил для группы звеньев 2 и 3, μ_F = 6,9 Н/мм

Определим реакцию из векторного уравнения , .

Из плана сил (на чертеже показана штриховой линией).

2.3.4. Силовой расчет ведущего звена

Рассмотрим силовой расчет ведущего звена 1 (рис. 2.10). Так как кривошип уравновешен, центр масс находится в точке O звена, то . При этом считается, что масса противовеса, расположенного от оси вращения на расстоянии , равна массе кривошипа m₁ и равнодействующая сила тяжести .

Со стороны отброшенного второго звена на первое действует реакция . Определим уравновешивающий момент из уравнения : ; .

Рис. 2.10. Силовой расчет ведущего звена (план сил, μF = 5,1 Н/мм)

Реакцию со стороны стойки на кривошип определим из векторного уравнения : .

Строим план сил в масштабе . Вектора-отрезки сил на плане сил в масштабе μ_F равны: , . Из плана сил .

2.4. Определение уравновешивающего момента методом возможных перемещений

В тех случаях, когда требуется определить уравновешивающий момент и уравновешивающую силу без предварительного определения реакций в кинематических парах, можно воспользоваться принципом возможных перемещений. Если система, состоящая из n звеньев, находится в равновесии, то сумма мгновенных мощностей всех сил и моментов, приложенных к звеньям механизма, должна равняться нулю. При этом уравновешивающий момент определяется из следующего уравнения:

,

где ω₁ – угловая скорость кривошипа, с^-1; F_i – силы, приложенные в характерных точках плана скоростей, перенесенные на план скоростей без изменения своего направления, Н; – проекции скоростей точек приложения сил на направление действия сил, мм; μ_V – масштаб плана скоростей, .

При этом целесообразно провести предварительную замену силы инерции и момента сил инерции на одну силу, приложенную в центре качения (рис. 2.11).

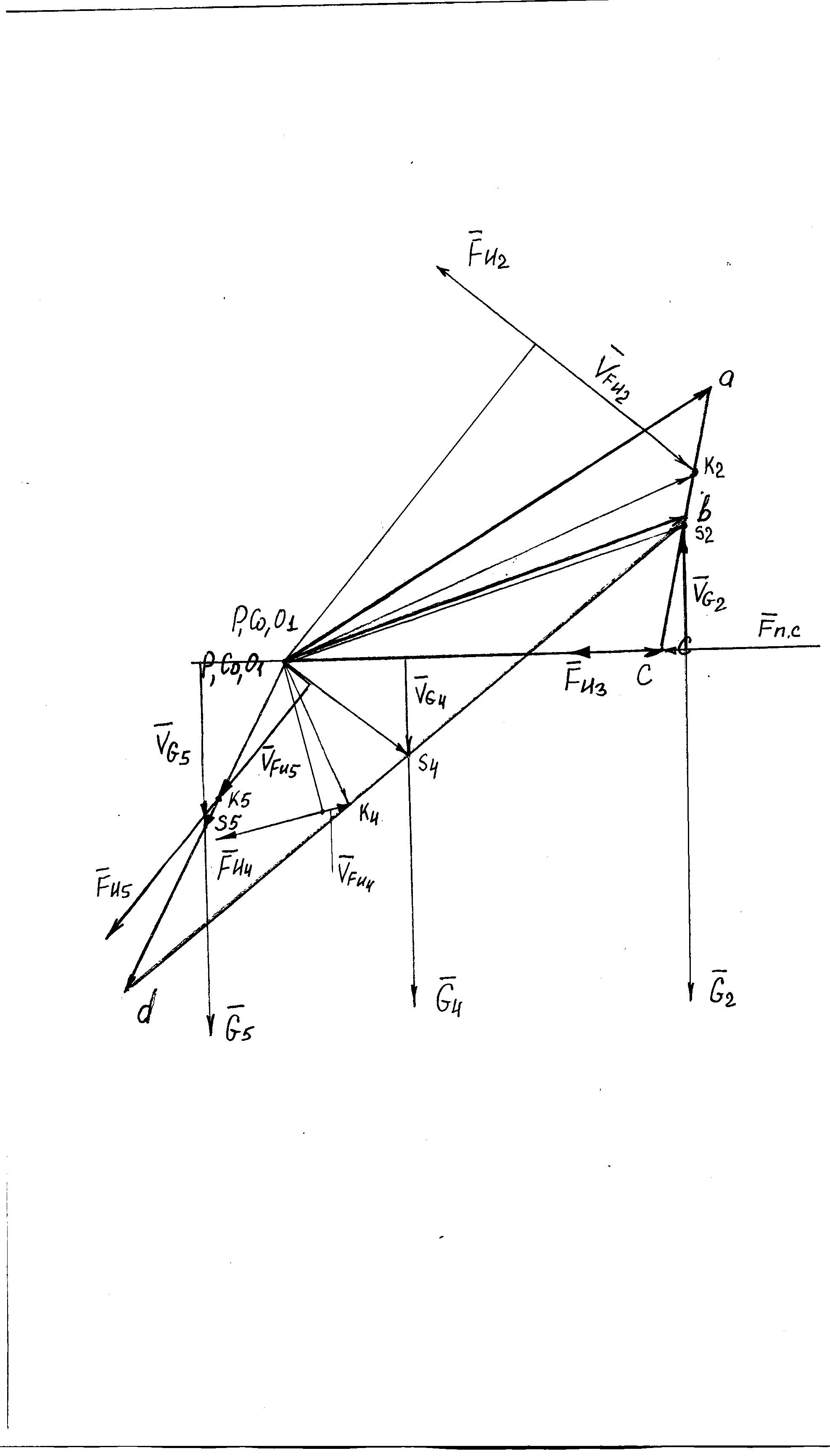
Рис. 2.11. Определение уравновешивающего момента методом возможных

перемещений, μ_V = 0,025 м/с·мм

Для проведения замены определим расстояния h_i (плечи пар сил) для каждого звена:

.

;

;

.

Величины плеч на чертеже равны:

;

;

.

Определим точки качения K_i на звеньях (рис. 2.6 и рис. 2.8). Основываясь на свойстве подобия плана скоростей и плана механизма, определим положения точек качения K_i на плане скоростей (рис. 2.11).

Для второго звена:

;

.

Для четвертого звена:

;

.

Для пятого звена:

;

.

В характерные точки плана скоростей (центры масс S_i, расположенные посередине звеньев, точки качения K_i) приложим силы тяжести и силы инерции. Силу полезного сопротивления приложим в точке С плана скоростей (рис. 2.11).

Определив проекции скоростей точек приложения сил на направление действия сил , найдем уравновешивающий момент

Учитывая, что произведения необходимо брать со знаком «плюс», если направления сил F_i и проекций скоростей совпадают, и со знаком «минус», если направления сил F_i и проекций скоростей противоположны. Получим

.

Знак «плюс» показывает, что направление уравновешивающего момента совпадает с направлением угловой скорости входного звена.

Относительная погрешность в определении уравновешивающего момента двумя методами составит:

.

Она не должна превышать 4%.

28