Начальная ордината графика ускорений определяется из формулы

.

Начальная и конечная точки графика за период цикла движения долж­ны иметь одинаковые ординаты.

Для проверки правильности построения графиков служат следующие зависимости между графиками функции (скорости) и графиками её производ­ной (ускорения):

1. максимальной или минимальной ординате графика скорости соот­ветствует нулевая ордината ускорений;

2. точке перегиба графика скорости соответствует максимум или ми­нимум графика ускорений.

При графическом дифференцировании заданы: масштаб времени , масштаб скорости , полюсное расстояние H, мм. Масштаб графика ускорений определяется по формуле

.

1.5. Графическое интегрирование

Графическое интегрирование является задачей, обратной дифференци­рованию.

Положим, что движение точки задано графиком ускорений (рис. 1.5, а) и требуется построить график скорости . Разбивая ось вре­мени t на ряд участков, заменяют внутри каждого участка переменное уско­рение постоянным средним ускорением, проводя горизонтальный отрезок с ординатой, изображающей это среднее ускорение так, чтобы площади высту­пающих и входящих углов были одинаковыми (рис. 1.5, а).

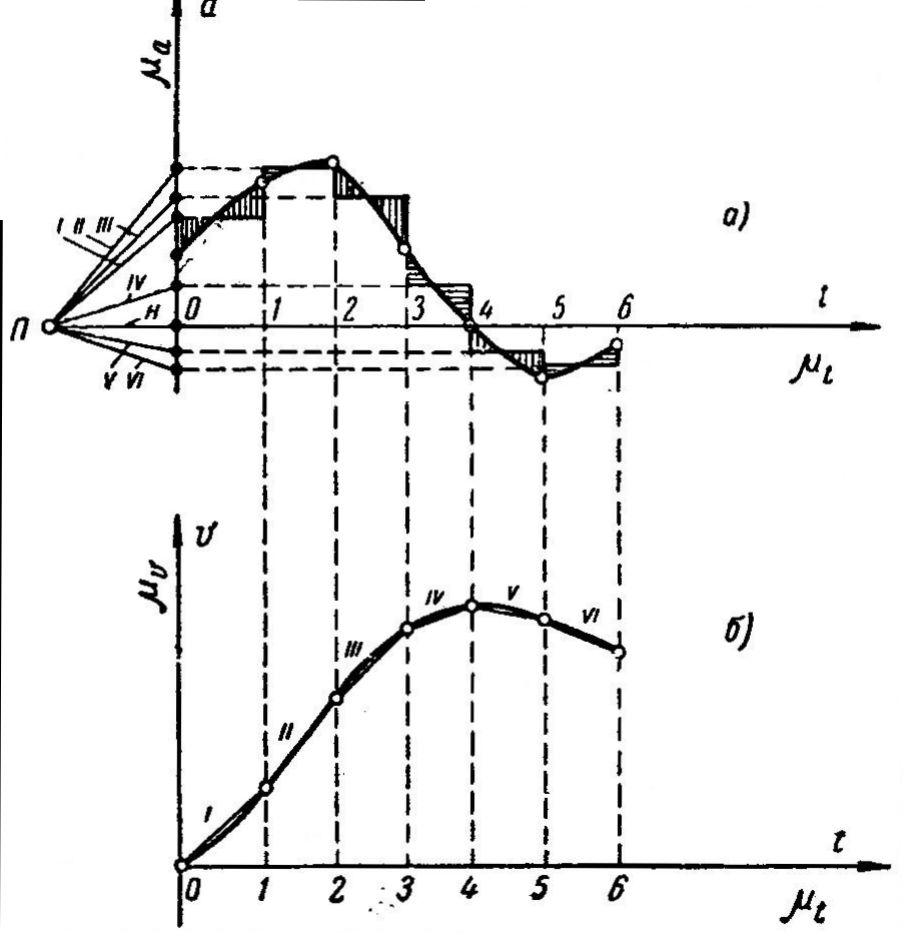
Рис. 1.5. Графическое интегрирование

Ординаты полученных средних ускорений сносят на ось ускорений и соединяют лучами I, II, III… с полюсом П, взятым на расстоянии H, мм, от начала координат.

На том же чертеже, ниже системы осей (a, t) строят систему осей (V, t) (рис. 1.5, б) и из точки O начала этих осей на соответствующих участках про­водят отрезки, параллельные лучам I, II, III и т.д. Затем строят первую ли­нию, которая приближенно представляет искомый график .

Так как график рекомендуется строить от крайних положений входного звена, в которых его скорость равна нулю, то график скорости строится от начала координат. Масштаб полученного графика связан с масштабом графика ускорений и полюсным расстоянием формулой

.

2. Силовой анализ рычажного механизма (графоаналитический метод)

2.1. Задачи и последовательность проведения силового анализа

Задачей силового анализа механизмов является определение сил, действующих на звенья механизма, и реакций в кинематических парах, а также уравновешивающих момента или силы на ведущем звене.

К заданным силам относятся: движущие силы, силы производственных сопротивлений, силы веса звеньев и условно силы инерции звеньев, зависящие от их масс и ускорений.

При проведении силового расчета пользуются методом кинетостатики, который заключается в том, что если к движущейся с ускорением системе, кроме внешних сил, добавить силы инерции, то все силы, действующие на систему, будут уравновешены и к ней могут быть применены теоремы статики.

В проекте силовой расчет производят для одного из двух положений механизма: внутри интервала рабочего хода с учетом сил производственных (полезных) сопротивлений, в интервале холостого хода без учета сил производственных (полезных) сопротивлений. Определение движущих сил или сил производственных сопротивлений производится по данным, приведенным в заданиях, индикаторных диаграммах, графиках сил полезных сопротивлений и т. п.

Для определения реакций в кинематических парах механизм разделяется на структурные группы. Воздействие других звеньев механизма на звенья отсоединенной группы заменяются силами реакций, каждую из которых удобно разложить по направлению звена (нормальную составляющую) и пер­пендикулярно этому направлению (тангенциальную составляющую).

Тангенциальные составляющие определяются из уравнений моментов сил, составленных для отдельных звеньев, входящих в структурную группу. Нормальные составляющие реакций определяются построением векторного многоугольника: геометрическая сумма сил, действующих на рассматриваемую структурную группу, должна равняться нулю.

Силовой расчет начинают с наиболее удаленной от входного звена структурной группы и заканчивают расчетом входного звена. К входному звену может быть приложен уравновешивающий момент или уравновешивающая сила. Если кривошипный вал соединен с двигателем, то в этом случае к валу приложен уравновешивающий момент , а реакция в опоре вала будет равна действию второго звена на кривошип (рис. 2.1).

Если кривошипный вал соединен с двигателем посредством зубчатой передачи, то в этом случае на звено АВ действует уравновешивающая сила со стороны сопряженного колеса под углом (90°- α_w) к линии центров колес (α_w – угол зацепления) (рис. 2.2, а); величина уравновешивающей силы F_у определяется из равенства

.

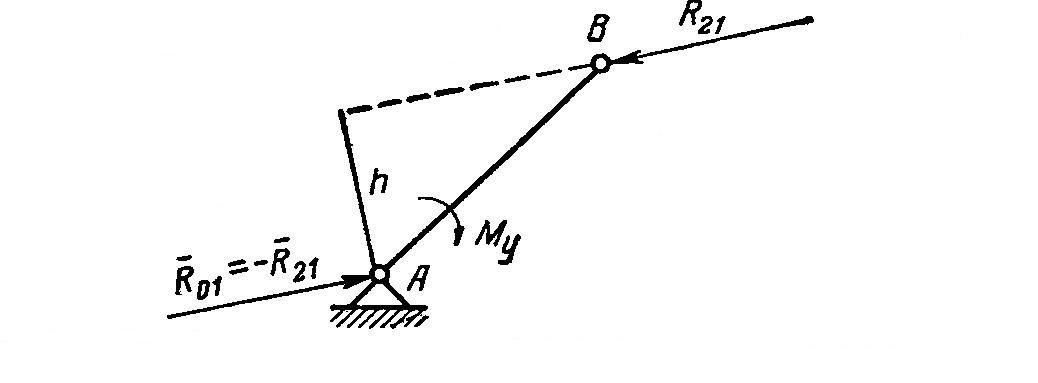
Рис. 2.1. К определению уравновешивающего момента

Рис. 2.2. К определению уравновешивающей силы

Реакция может быть определена из векторного уравнения , в котором имеется один неизвестный вектор . Графическим решением этого уравнения является треугольник сил, показанный на рис. 2.2, б.