3.1.3 Графический метод кинематического исследования планетарной зубчатой передачи.

Способ графического определения передаточного отношения планетарного механизма состоит в построении и исследовании картин (планов) линейных и угловых скоростей.

Изображаем кинематическую схему механизма с использованием масштабного коэффициента длины, определяемого по формуле:

где z – число зубьев колеса;

m – модуль зацепления.

Диаметр делительной окружности определяется по формуле: D=mZ.

Построение картины линейных скоростей.

Чтобы построить картину линейных скоростей, проведем параллельно плоскости вращения колес вертикальную прямую, на которую спроектируем оси зубчатых колес (О₁, О₃), оси сателлита (О_Н1, О_Н2) и все полюса зацепления (12, 34, 52', 5'4'); от точки 12 полюса зацепления колес 1 и 2 проводим прямую ₁, изображающую в масштабе _V окружную скорость точки на начальной (делительной) окружности колеса 1, далее соединив точки О₁ и конец вектора ₁ получим линию распределения скоростей звена 1.

Скорость точки О₁ для колеса z₁ равно 0, скорость ₁ можно найти по формуле:

Скорость точки 52' равна нулю, следовательно, для звена Z₂-Z_2' известны скорости двух точек, и можно провести линию распределения линейных скоростей этого звена, соединив точки 52' и конец вектора ₁.

Из точки О_Н1 опустим перпендикуляр до пересечения с линией распределения звена Z₂-Z_2'. Полученный отрезок _H1 определяет окружную скорость оси звена 2 и окружную скорость водила Н₁. Соединив точки О₃ и конец вектора _H1, получим линию распределения скоростей водила Н₁ и Z₃, так как Z₃ и Н₁ являются единым звеном. К прямой О₃-конец вектора _H1 восстановим перпендикуляр из точки 34, полученный вектор ₄ определяет окружную скорость Z₄, Z_4', соединив точки 5'4' и конец вектора ₄ получим линию распределения скоростей звена Z₄-Z_4'. К прямой 5'4'-конец вектора u₄ восстановим перпендикуляр из точки О_Н2, полученный вектор _H2 определяет окружную скорость водила Н₂.

Масштабный коэффициент картины линейных скоростей:

Построение картины угловых скоростей.

Проведем горизонтальную прямую О и на произвольном расстоянии от точки О по вертикали отложим точку P_ (О P_=70 мм), считая эту точку полюсом и проведя из нее лучи параллельно линиям распределения линейных скоростей звеньев 1; 4; Н₁; Н₂, получаем на пересечении с линией О точки Н₁, Н₂, 4, 1.

Масштабный коэффициент картины угловых скоростей:

Измерив на картине угловых скоростей отрезки О1 и ОH₁ (а также О4 и ОН₂) и взяв их отношение, находим:

;

Вычисляем погрешность в вычислении передаточных отношений:

3.2 Построение геометрической картины зацепления эвольвентных зубьев.

Рассмотрим внешнее эвольвентное зацепление.

Эвольвента окружности получается, если по неподвижному кругу данного радиуса перекатывать прямую без скольжения. Любая точка этой прямой прочертит эвольвенту в плоскости круга. Окружность, по которой перекатывается прямая, называется основной окружностью, а прямая – производящей прямой.

Пара зубчатых колес, находящихся в зацеплении, всегда имеет соприкасающиеся окружности, которые при вращении этих колес перекатываются друг по другу без скольжения. Эти окружности касаются в полюсе зацепления П и называются начальными (r, мм).

Окружность изготовленного зубчатого колеса, по которой производится деление цилиндрической заготовки на z равных частей, называется делительной окружностью, где z- число зубьев зубчатого колеса. Зубчатые колеса, нарезаемые без смещения режущего инструмента, называются нулевыми. У нулевых зубчатых колес начальный r (мм) и делительный r окружности совпадают. Окружность, ограничивающая вершины готовых зубьев, называется окружностью выступов (r_a, мм).

Окружность, ограничивающая глубину впадин со стороны тела колеса, называется окружностью впадины (r_f). Расстояние между двумя одноименными точками двух соединенных зубьев, измеренное по делительной окружности, называется шагом зацепления p (мм).

Отношение P/ называется модулем зацепления и обозначается m:

мм

Модуль зацепления является основным геометрическим параметром зубчатого зацепления. По известному модулю и числу зубьев можно определить все остальные геометрические параметры зубчатого колеса.

Коэффициентом торцевого перекрытия называется отношение длины k (мм) дуги зацепления к длине шага P (мм) по начальным окружностям колес:

.

Длина дуги зацепления k (мм) определяется по формуле:

(мм),

где AB – длина активной части линии зацепления. Тогда коэффициент торцевого перекрытия:

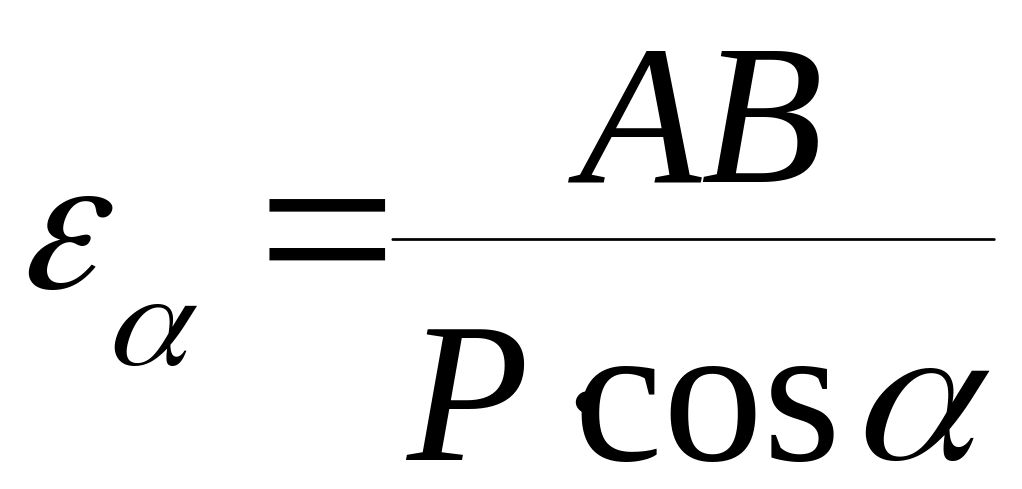
Коэффициент перекрытия характеризует собой плавность работы зацепления и показывает число пар зубьев одновременно находящихся в зацеплении.

Коэффициент перекрытия может быть определен аналитически по формуле:

,

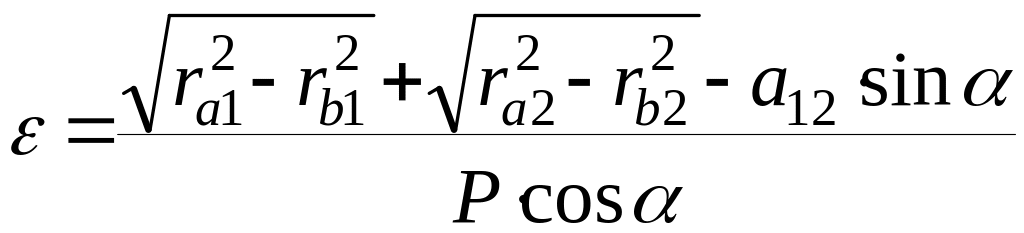где r_a1, r_a2 – радиусы окружностей выступов соответственно шестерни и колеса;

r_b1, r_b2 – радиусы основных окружностей соответственно шестерни и колеса;

– межосевое расстояние;

P – шаг зубьев;

 – профильный угол инструментальной рейки.

Дано:

число зубьев шестерни z₁=18;

число зубьев колеса z₂=19;

модуль зацепления m=30.

Радиусы (r, мм) делительных (начальных) окружностей:

(мм);

(мм);

(мм).

Радиусы основных окружностей (r_b, мм):

(мм), =20°;

(мм);

(мм).

Радиусы (r_f, мм) окружностей впадин:

(мм);

h_a^*+c^*=1,25;

(мм);

(мм).

Шаг зубьев (P, мм) по делительной окружности:

(мм);

P=3,14^.30=94,25 (мм).

Высота головки зуба (h_a, мм):

(мм).

Высота ножки зуба (h_f, мм):

(мм);

h_f=30^.1,25=37,5 (мм).

Высота зуба (h, мм):

h=h_a+h_f (мм);

h=30+37,5=67,5 (мм).

Радиусы окружностей выступов (r_a, мм):

r_a=r_f+h (мм);

r_a1=232,5+67,5=300 (мм);

r_a2=247,5+67,5=315 (мм).

Толщина зуба по делительной окружности (S_t, мм):

(мм);

(мм).

Межосевое расстояние ( , мм):

(мм);

(мм).

Коэффициент перекрытия:

;

.

Построение геометрической картины зацепления эвольвентных зубьев.

Выбираем масштабный коэффициент длины, исходя из условия, чтобы высота зуба на чертеже была не менее 50 мм

,

где m – модуль зацепления, мм;

z₁ – число зубьев колеса 1;

О₁П – отрезок на чертеже (мм), изображающий радиус делительной окружности.

Вычерчиваем профили зубьев в следующей последовательности:

а) На линии центров полюсов от точки П (полюса зацепления) откладываем радиусы начальных окружностей r₁ и r₂ и проводим эти окружности.

б) Строим основные окружности радиусами r_b1 и r_b2. Проводим прямую N₁N₂ являющуюся теоретической линией зацепления. Для этого проводим радиусы основных окружностей под углом =20° к прямой, соединяющей центры колес. Эти радиусы в пересечении с основными окружностями дадут точки N₁ и N₂. Если центры колес выходят за пределы чертежа, построение ведут в таком порядке: строим прямую КК, касательную к начальным окружностям; от нее проводим прямую под углом =20°. Эта прямая будет касаться основных окружностей в точках N₁ и N₂.

в) Строим эвольвенты, которые описывает точка П прямой при перекатывании ее по основным окружностям. При построении эвольвенты первого колеса (шестерни) отрезок N₁П делим на 4 равные части (П-1, 1-2, 2-3, 3-N₁) и из точки 3 проводим дугу радиусом ₁=3П до пересечения в точке О' с основной окружностью, тогда N₁O'=N₁П.

На прямой ПN₁ за точкой N₁ откладываем отрезки (4-5=5-6=6-7=7-8=П-1). Дугу N₁O' делим на такое же число равных дуг (O'-I'=I'-2'=2'-3'=…) Откладывая эти дуги за точку N_1, получим дуги ('-5'='-6'=…), равные дуге O'-I'.

Через точки 1'; 2'; 3'; … на основной окружности проводим перпендикуляры к соответствующим радиусам O₁-1'; O₁-2'; O₁-3';…,

где О₁ – центр вращения колеса Z₁. На этих перпендикулярах (они являются касательными к основной окружности) из точек 1'; 2'; 3';….. откладываем отрезки, равные отрезкам 1-П, 2-П, 3-П, … с теоретической линии зацепления N₁N₂. Соединяя последовательно полученные точки плавной кривой, получаем эвольвенту для первого зубчатого колеса. В той же последовательности строим эвольвенту для второго зубчатого колеса.

г) Строим окружности выступов обоих колес r_a1 и r_a2. Для более точного построения целесообразно отложить с использованием масштабного коэффициента длины _l высоты головок на линии центров колес от точки П.

Построив окружности выступов, найдём точки их пересечения с соответствующими эвольвентами – крайние точки на профилях головок.

д) Строим окружности впадин колес радиусами r_f1 и r_f2. Здесь также целесообразно предварительно отложить высоты ножек с использованием масштабного коэффициента длины от точки П.

Полный профиль ножки зуба состоит из эвольвентной части и переходной кривой (галтели), которая соединяет эвольвентную часть с окружностью впадин. Профиль ножки у основания зуба строим следующим образом: из центра вращения колеса О₁ проводят радиус О₁О' до начала эвольвенты, а затем у основания зуба делают закругление радиусом r_fm''=0,38m.

е) От точки П откладываем на делительной окружности дуги: влево ПЕ и вправо ПF, равные каждая длине шага P. От точек П, Е и F влево откладываем дуги ПМ ,ER, FH, равные каждая толщине зуба по делительной окружности.

Делим дуги ПМ, ER и FH пополам. Соединяя полученные точки на делительной окружности с центром О₁, получаем оси симметрии зубьев. После этого вырезаем из твердой бумаги шаблон половины зуба, которым пользуемся для построения остальных зубьев. Аналогично строим 3 зуба второго колеса.