4. Время жизни неосновных носителей, диффузионная длина.

В процессе движения зарядов в полупроводниках происходят релаксационные процессы, связанные с генерацией и рекомбинацией зарядов. Для того чтобы приборы работали в микроволновом диапазоне, необходимо выполнить условие 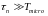во временной области и 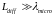в пространственной.

Практические измерения времени жизни носителей заряда в полупроводниках показали величину 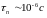. Пространственный интервал, связанный с этой величиной называется диффузионной длиной и рассчитывается с помощью следующего соотношения:

,

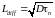где 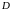-коэффициент диффузии.

Подстановка реальных значений для 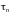и показывает, что условия в пространственной и во временной области выполняются.

10.2. Макроскопическая система уравнений полупроводниковой электроники

Усиление и генерация электромагнитных колебаний полупроводниковыми приборами СВЧ осуществляется за счет взаимодействия носителей заряда, движущихся в объеме полупроводника, с высокочастотным электромагнитным полем. Как было показано в гл.1 для математического описания этого взаимодействия используют систему, состоящую из уравнения Больцмана и уравнений Максвелла. В практически важных случаях не требуется уравнений на основе , отличающие степенью строгости. В данном рассмотрении используется мдетализация процессов токопереноса и для анализа бывает достаточно макроскопических параметров системы. В этих случаях уравнения (1.22-1.24) могут быть сведены к более простым уравнениям переноса:

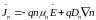; (10.12)

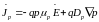; (10.13)

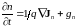; (10.14)

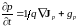. (10.15)

Уравнения (10.14) и (10.15) называются уравнениями непрерывности. К этой системе необходимо добавить уравнение Пуассона:

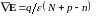(10.16)

и выражение для плотности полного тока:

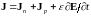. (10.17)

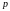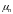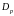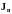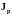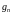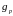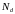В этих уравнениях и - концентрации; и - подвижности; и - коэффициенты диффузии; и - плотности токов; и - скорости генерации - рекомбинации электронов и дырок соответственно; - эффективная концентрация легирующей примеси ( и 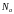- концентрации доноров и акцепторов); 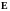- напряженность электрического поля; 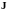- плотность тока; 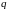- заряд электрона; - диэлектрическая проницаемость полупроводника.

Область применимости системы уравнений (10.12-10.17) ограничивается приближениями, которые были сделаны при ее выводе. К ним относятся:

1. Предположение о непрерывности функци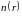й и 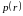, что не позволяет рассматривать процессы в областях, размеры которых меньше дебаевского радиуса экранирования (длины Дебая). Это обстоятельство затрудняет анализ процессов в областях с малой протяженностью и с низкой концентрацией носителей заряда (например, в базовой области микроволнового - транзистора).

2. При выводе принято т.н. локальное приближение, когда скорость носителей определяется полем в данной точке. Другими словами, скорость определяется приложенной силой в данной точке. Однако, для изменения скорости под действием силы требуется время. Характерным масштабом изменения скорости будет время порядка времени релаксации по импульсу 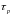. (см. разд.10.1.1). Стационарное значение скорости установится за время релаксации энергии 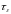. В связи с этим рассматриваемая система уравнений плохо описывает процессы в полупроводнике на частотах свыше .

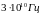3. В уравнениях (10.12-10.13) не учитываются как внешнее магнитное поле, так и собственное магнитное поле токов, протекающих в полупроводнике. Это исключает из рассмотрения целый ряд физических явлений, которые, однако, не играют существенной роли в рассматриваемых полупроводниковых приборах.

Свойства системы уравнений (10.12-10.17) определяются входящими в нее величинами, характеризующими среду. Рассмотрим эти величины более подробно. Подвижности электронов и дырок устанавливают связь между напряженностью электрического поля и дрейфовой скоростью носителей:

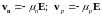. (10.18)

В таких материалах, как Ge, Si, GaAs, подвижности являются скалярными величинами, зависящими от напряженности электрического поля , концентрации примеси 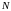и температуры 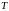. У этой зависимости наблюдается насыщение дрейфовой скорости в полях выше 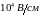(рис.10.9), связанное с рассеянием носителей заряда на оптических фононах. Скорость насыщения 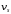в большинстве материалов близка к .

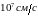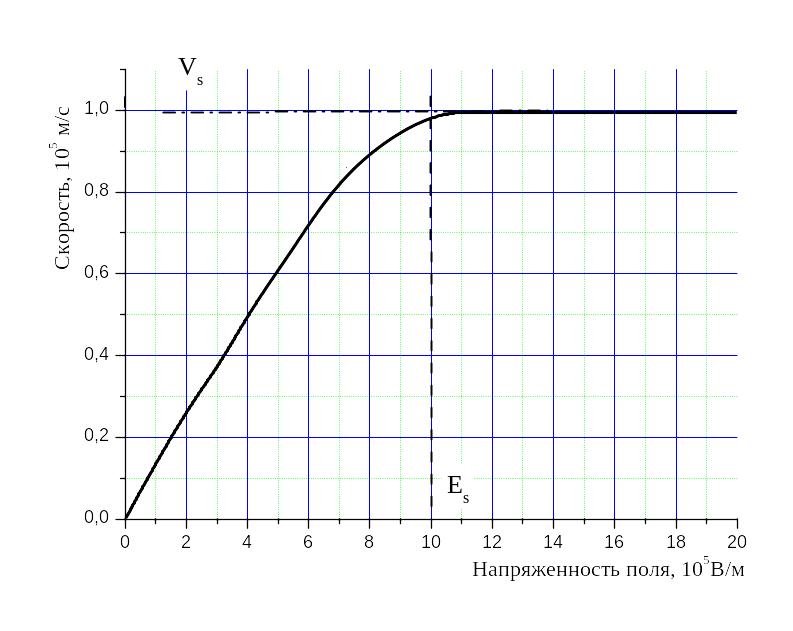
Рис. 10.9. Зависимость дрейфовой скорости носителей заряда от напряженности электрического поля для кремния.

Для некоторых материалов, таких, как GaAs, InP и т.п., зависимость скорости электронов от напряженности поля имеет вид, показанный на рис.10.10. Кроме того, при не слишком больших температурах имеет место участок с отрицательной дифференциальной подвижностью (ОДП) , возникающей за счет междолинных переходов электронов. Заметим, что у дырок ОДП не наблюдается.

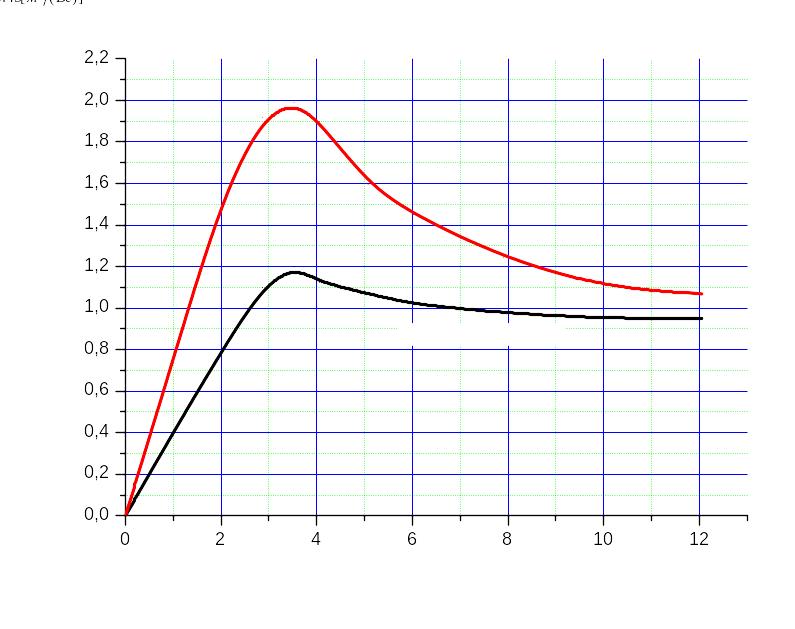
Рис.10.10. Зависимость дрейфовой скорости электронов от напряженности электрического поля для арсенида галлия при 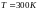и при двух значениях малосигнальной подвижности .

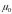Коэффициенты диффузии 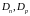также зависят от параметров среды. Они связаны с подвижностями известным соотношением Эйнштейна в условиях термодинамического равновесия:

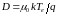, (10.19)

где - эффективная температура носителей, определяемая их средней кинетической энергией 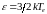. В сильных полях температура носителей может существенно отличаться от температуры решетки .

Скорость генерации - рекомбинаци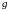и определяется как число пар носителей, возникших (исчезнувших) в единице объема полупроводника за единицу времени. Генерация и рекомбинация в полупроводнике могут происходить по различным причинам. Важнейшие из них - тепловая генерация и рекомбинация на рекомбинационных центрах. Для случая, когда рекомбинационный центр имеет один энергетический уровень, скорость тепловой генерации - рекомбинации определяется формулой

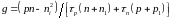, (10.20)

где 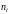- собственная концентрация носителей заряда; 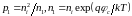, 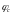- энергетический уровень рекомбинационного центра; 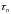и - времена захвата электронов и дырок. Наряду с тепловой генерацией в полупроводниковых приборах важную роль играет генерация носителей за счет ударной ионизации. Введем коэффициенты ударной ионизации для электронов 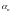и дырок 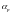, численно равные числу пар носителей, образованных электроном (дыркой) на пути единичной длины. Определим скорость генерации за счет ударной ионизации:

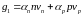.(10.21)

Зависимость коэффициентов ионизации от напряженности электрического поля выражается формулой

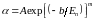, (10.22)

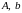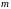где величины и определяются сортом носителей и материалом полупроводника. В большинстве полупроводников ударная ионизация становится заметной в полях, превышающих .

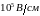Таким образом, система уравнений (10.12-10.17) является нелинейной, что весьма затрудняет ее решение в случае достаточно сильных электрических полей.

Для решения этой системы уравнений необходимо знать начальные и граничные условия для концентрации подвижных носителей, плотностей токов и поля. В качестве начальных обычно задаются условия термодинамического равновесия 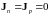, , 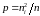(для полупроводников - типа), 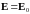, где 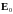- заданное поле в момент времени . Тип граничных условий определяется свойствами границ образца. Так, на границе полупроводник - диэлектрик выполняются условия:

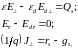
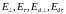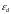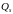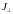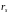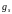где - нормальные и касательные к поверхности раздела составляющие напряженности электрического поля и тока в полупроводнике и диэлектрике; - диэлектрическая проницаемость диэлектрика; - поверхностный заряд; - нормальная составляющая плотности тока; и - скорости поверхностной рекомбинации и генерации.

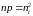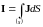На границе полупроводник-металл имеет место термодинамическое равновесие . Обычно задается также разность потенциалов между выводами прибора или ток через прибор , где 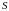- площадь контактных поверхностей.