Питання 4. Елементи математичної статистики Методичні рекомендації:

Математична статистика – наука про планування і проведення випадкових експериментів та аналіз їх результатів методами теорії ймовірності. Об’єктом статистичного дослідження є одна або кілька випадкових величин, які називаються спостережуваними величинами.

Генеральною сукупністю називають множину значень спостережуваної випадкової величини .

У результаті випробувань дістають вибірку (вибіркову сукупність) спостережених значень з генеральної сукупності. Якщо спостережені значення розташувати у порядку їх зростання, то дістанемо варіаційний ряд

де – кількість спостережених значень вибірки, що дорівнюють , , а – обсяг вибірки. При цьому числа називають варіантами, – їх абсолютними частотами, а – їхніми відносними частотами або статистичними ймовірностями, причому .

Статистичним розподілом вибірки називається перелік варіант та відповідних їм частот або відносних частот, тобто

			…
			…

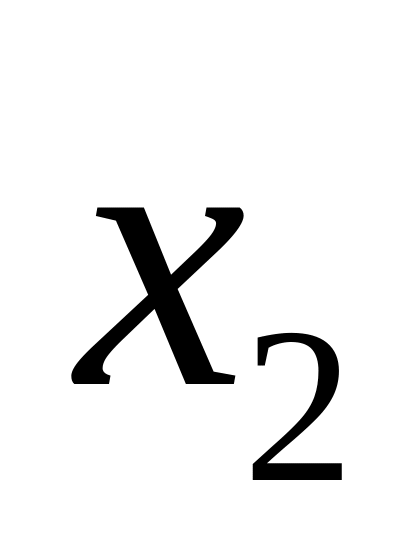
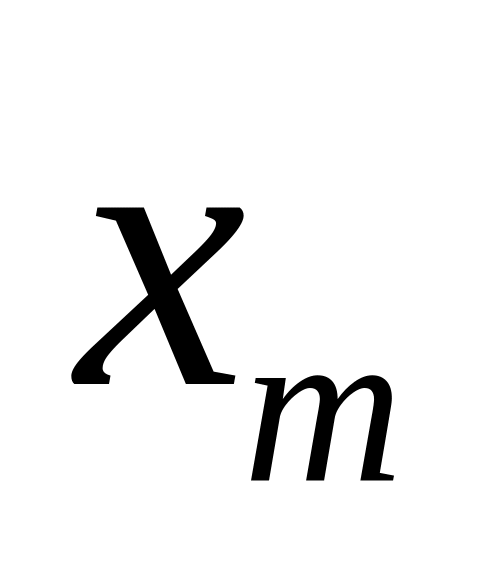
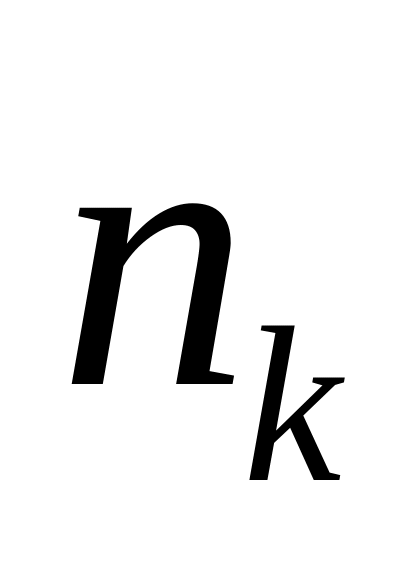
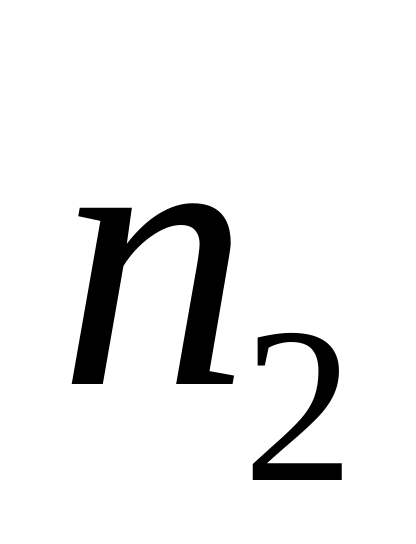
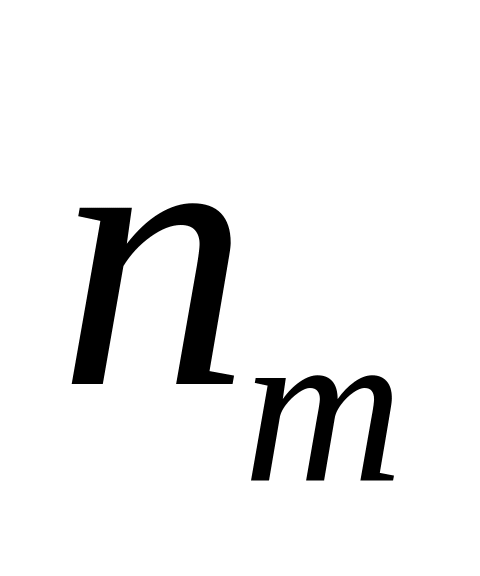
або

			…
			…

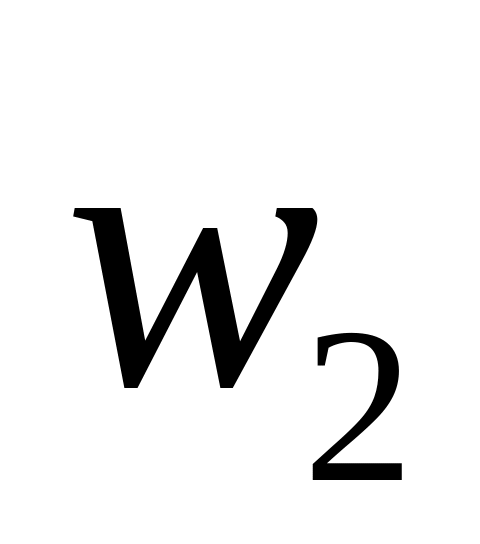
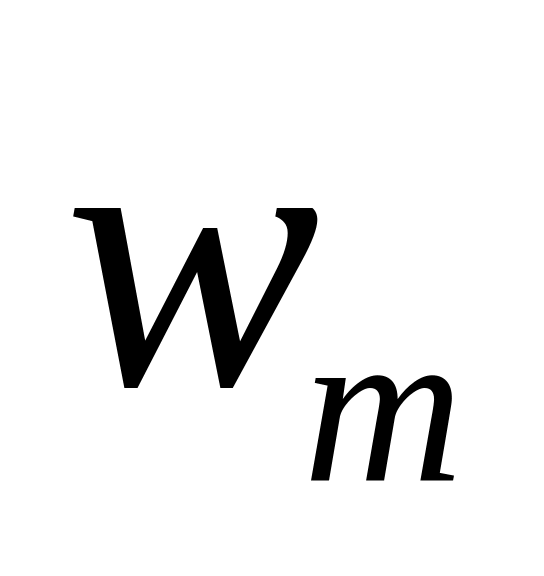
Де – об’єм вибірки і .

Нехай є статистичний розподіл частот деякої ознаки . Позначимо через загальну кількість спостережень, тобто об’єм вибірки; – кількість спостережень, при яких спостерігалися ознаки . Тоді відносна частота події дорівнює . Якщо змінюється, то може змінюватися відносна частота, тобто є функцією від . Ця функція знаходиться емпіричним (дослідним) шляхом, тому її називають емпіричною.

Означення: Емпіричною функцією розподілу (або функцією розподілу вибірки) називається функція , яка визначає для кожного значення відносну частоту події .

Математично це означення має вигляд: .

Емпірична функція розподілу має такі властивості:

1. ;

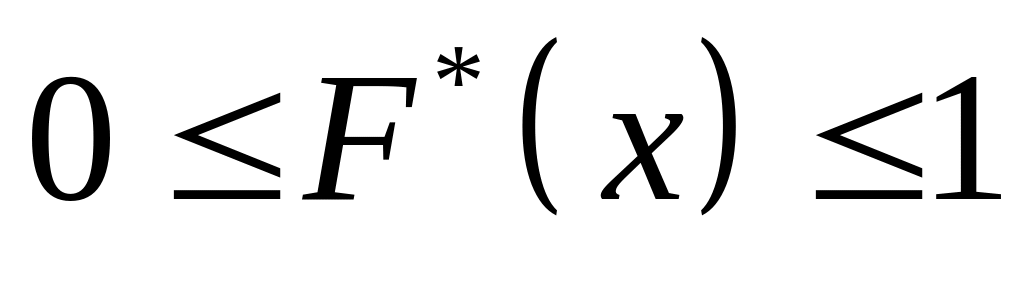2. – зростаюча функція;

3. 

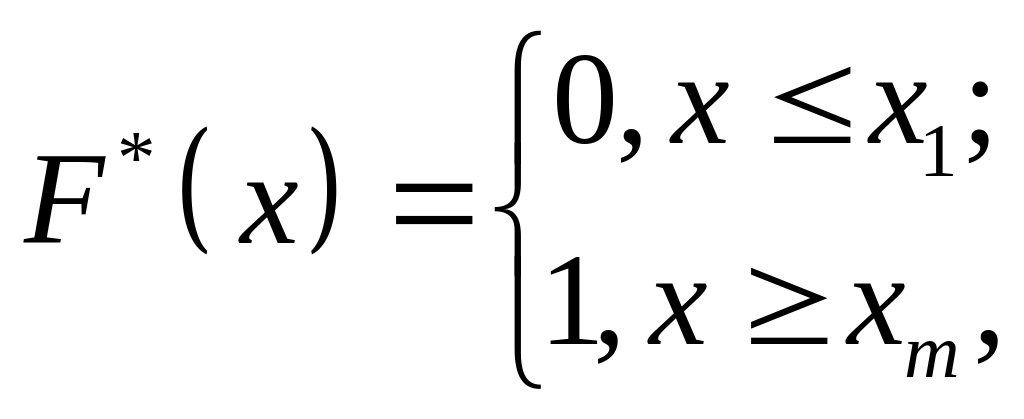
Де – найменша варіанта, – найбільша варіанта.

Полігоном частот називається ламана, відрізки якоїх з’єднують точки .

Полігоном відносних частот називається ламана, відрізки якої проходять через точки .

До числових характеристик вибірки відносяться:

1. Мінімальне 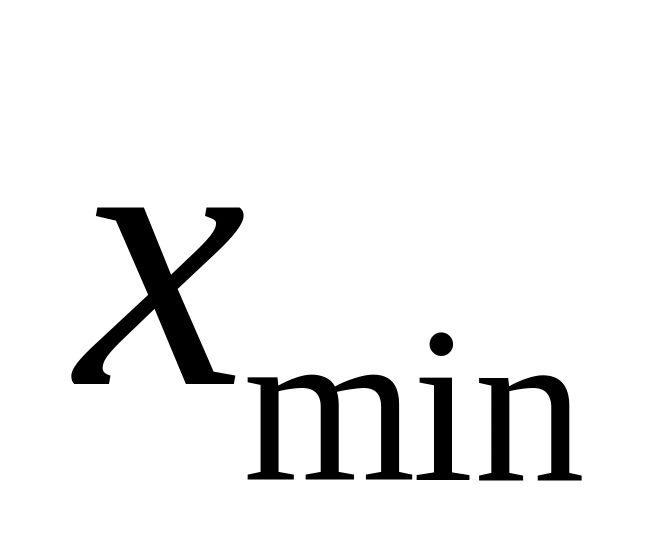і максимальне 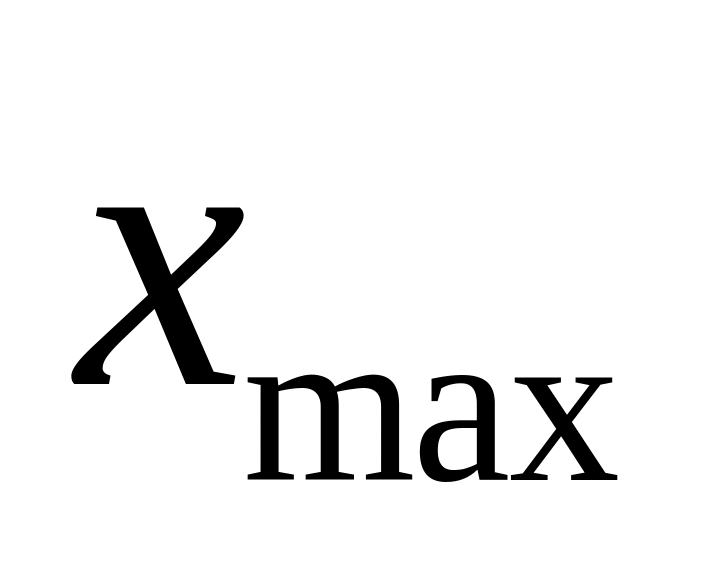спостережені значення;

2. Розмах вибірки ;

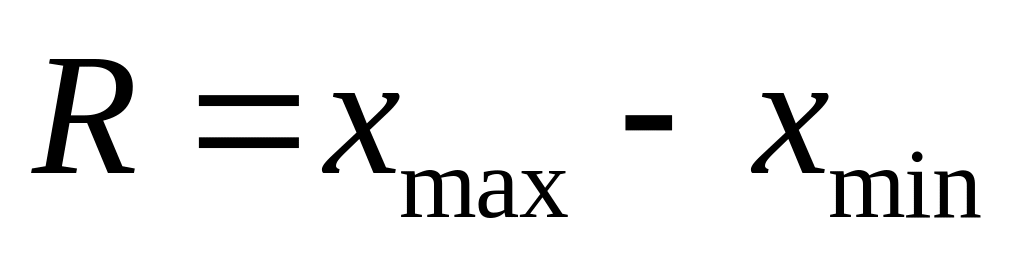3. Мода 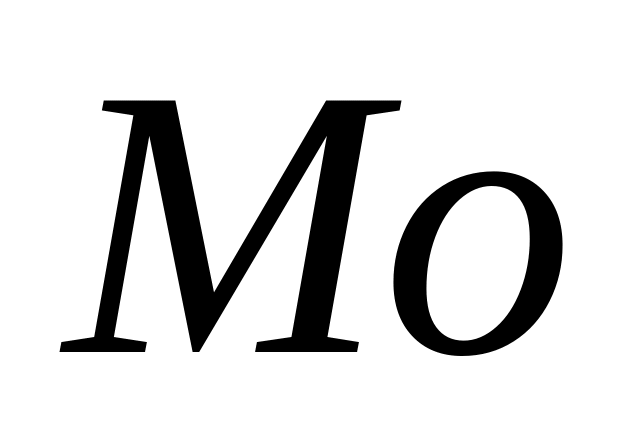– варіанта з найбільшою частотою у статистичному ряді розподілу частот;

4. Медіана – така точка проміжку 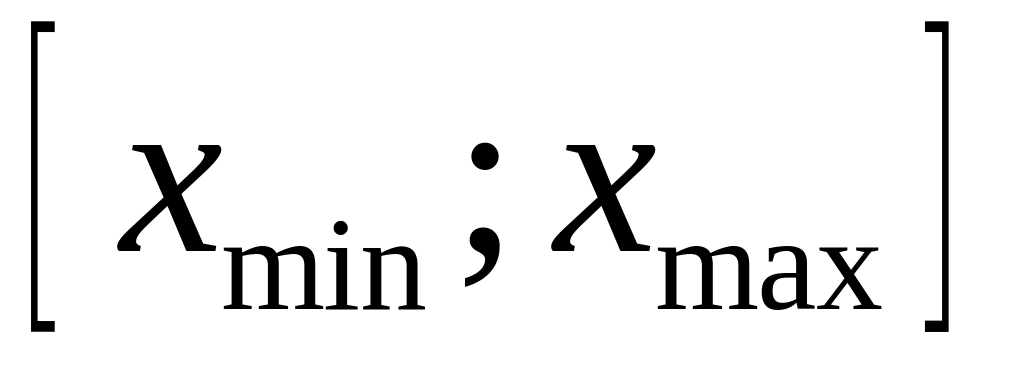, що ймовірність попадання спостереженого значення злііва від дорівнює ймовірності попадання спостереженого значення справа від , тобто медіана ділить варіаційний ряд навпіл.

5. Середнє арифметичне, або статистичне середнє, спостережених значень ;

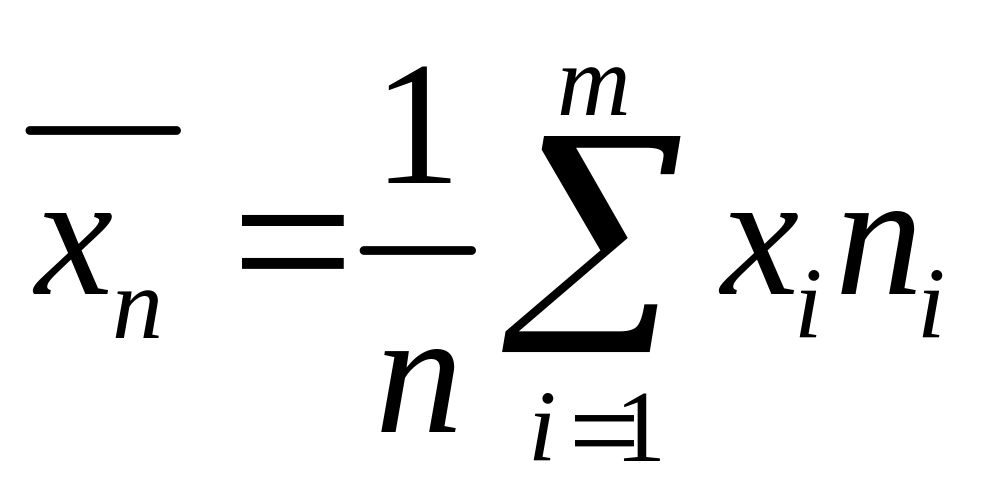6. Середнє гармонічне спостережених значень

7. ;

8. Середнє геометричне спостережених значень ;

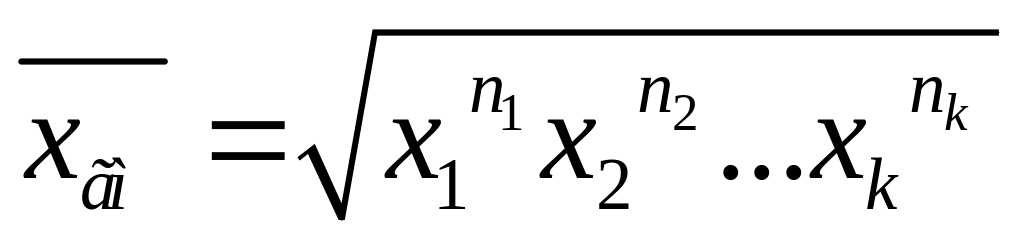9. Середнє квадратичне спостережених значень ;

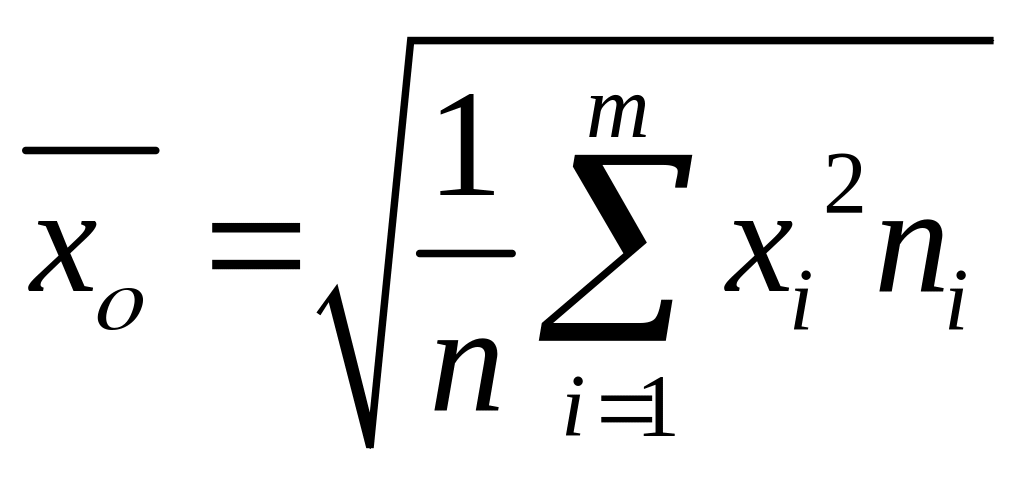10. Статистична дисперсія ;

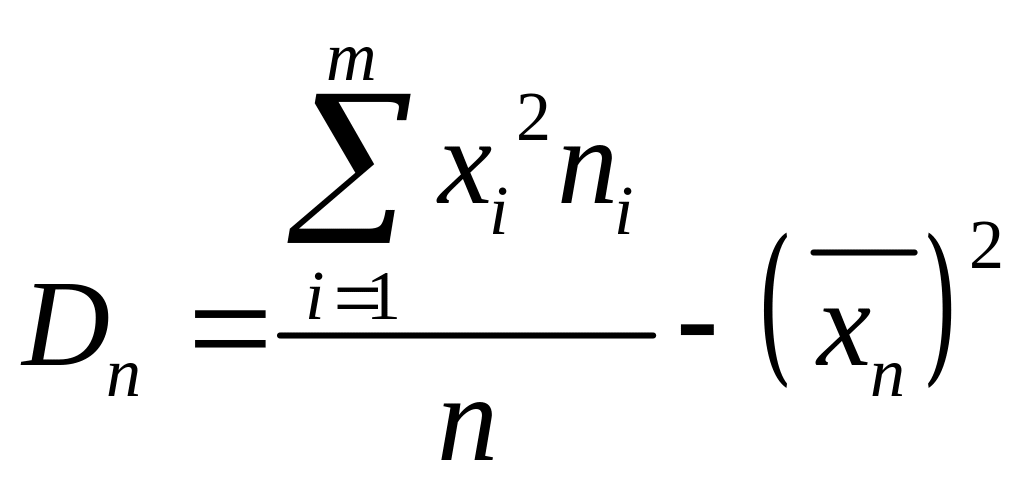11. Виправлена статистична дисперсія ;

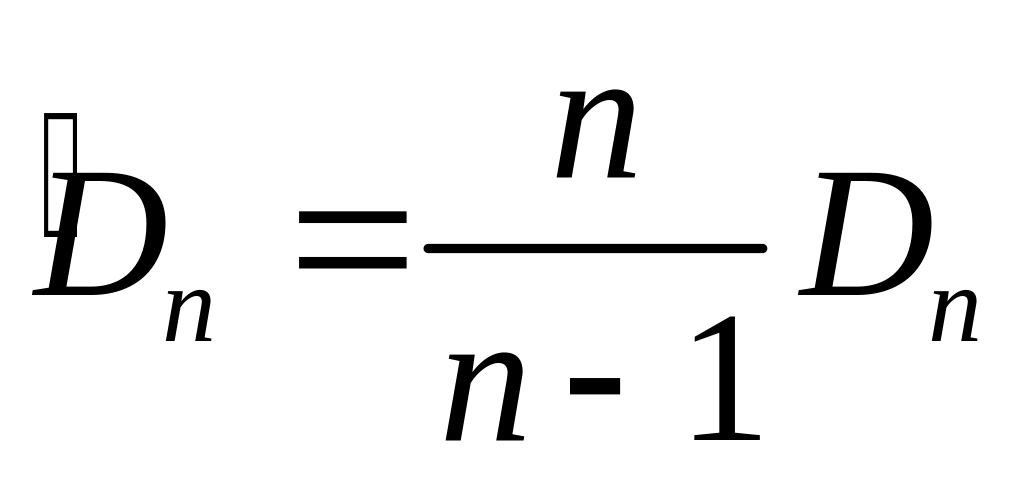12. Статистичне середнє квадратичне відхилення .
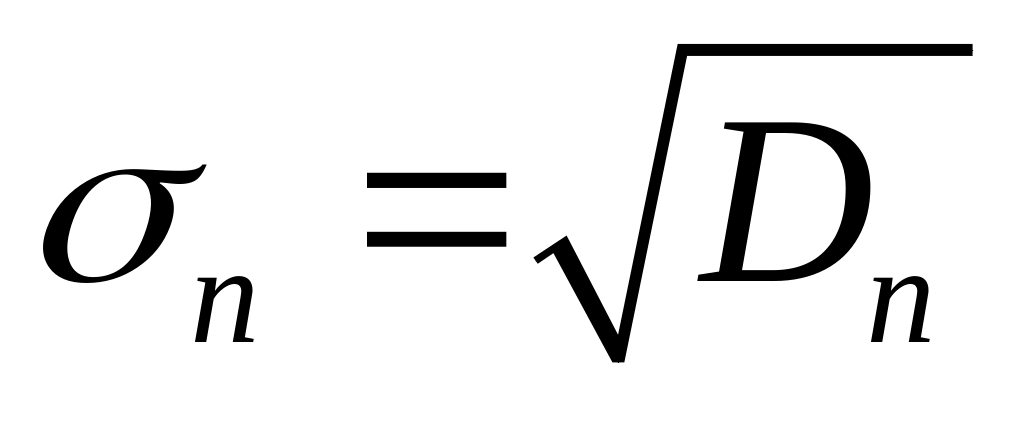