Література:

1. Лейфура В.М. та ін. Математика: Підручник для студентів екон. спеціальностей вищ. навч. закладів І-ІІ рівнів акредитації / В.М. Лейфура, Г.І. Городницький, Й.І. Файст; За ред. В.М. Лейфури. – К.: Техніка, 2003 – 640 с.

2. Кулян В.Р. и другие. Математическое программирование (с элементами информационных технологий): Учеб. Пособие/ В.Р. Кулян, Е.А. Юнькова, А.Б. Жильцов. – К.: МАУП, 2000

3. Васильченко І.П. Вища математика для економістів: Підручник – К.: Знання-Прес, 2002, 454 с.

Розділ 5

Тема: Диференціальне та інтегральне числення

САМОСТІЙНА РОБОТА № 5

Питання 1. Означення та економічний зміст похідної та диференціала.

Методичні рекомендації:

Нехай на деякому проміжку задано функцію у = f (x). Візьмемо будь-яку точку і надамо х довільного приросту ∆х такого, щоб також належала проміжку . Знайдемо приріст функції .

Означення: Похідною функції у = f (х) в точці х називається границя відношення приросту функції в цій точці до приросту аргументу , коли приріст аргументу прямує до нуля.

Похідна функції в точці х позначається одним із таких символів:

.

Таким чином, за означенням

.

Якщо в деякій точці х: , то похідна в цій точці називається нескінченною.

Якщо границя в деякій точці х не існує, то не існує в цій точці і похідної.

Значення похідної функції в точці позначається одним із таки символів:

Означення: Операція знаходження похідної від функції називається диференціюванням цієї функції.

Означення: Функція f(х) називається диференційованою в точці х₀, якщо в цій точці вона має похідну .

Означення: Функція називається диференційованою на деякому інтервалі , якщо вона є диференційованою у кожній точці цього інтервалу.

Зв’язок між неперервністю функції в точці і диференційованістю її в цій точці встановлює така теорема.

Теорема: Якщо функція диференційована в точці х₀, то вона в цій точці неперервна.

Обернене твердження неправильне: існують неперервні функції, які в деяких точках не є диференційованими. Це означає, що неперервність функції в точці є тільки необхідною умовою диференційовності функції в даній точці.

Геометричний зміст похідної виражає твердження:

Твердження: Графік функції , визначеної і неперервної в деякому околі точки , що має похідну в точці , в точці має дотичну, кутовий коефіцієнт якої дорівнює .

Поняття диференціала тісно пов’язане з поняттям похідної, і є одним з найважливіших в математиці. Диференціал наближено дорівнює приросту функції і пропорційний приросту аргументу.

Термін “диференціал” (від латинського слова differentia - різниця) ввів у математику Лейбніц.

Нехай функція диференційована в точці , тобто в точці має похідну . Тоді , де при , звідки . Перший з доданків лінійний відносно і при та є нескінченно малою одного порядку з , тому що 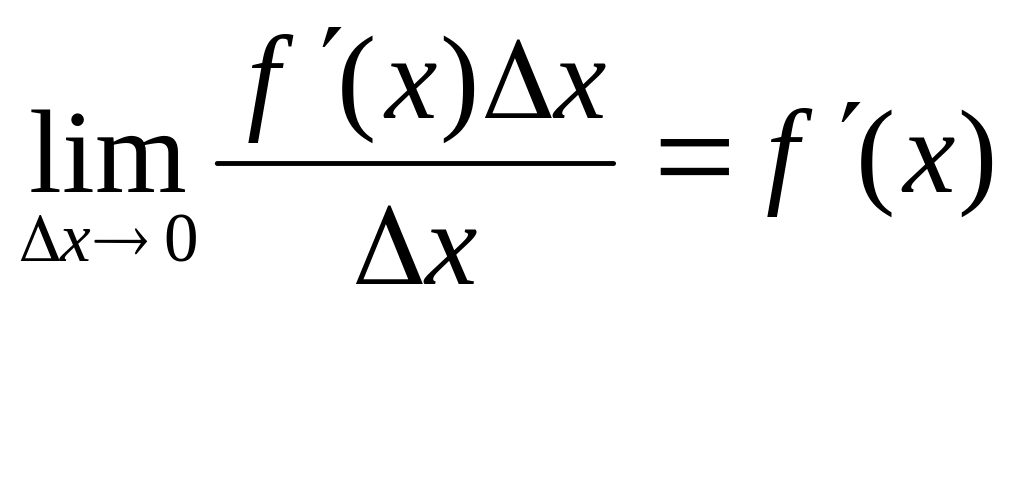. Другий доданок – нескінченно мала вищого порядку, ніж , тому що . Цей доданок не є лінійним відносно , тобто містить в степені, вищому від одиниці. Таким чином, перший доданок є головною частиною приросту функції, лінійною відносно приросту аргументу.

Означення: Диференціалом функції в точці називається головна, лінійна відносно , частина приросту функції в цій точці:

, (1).

Диференціал називають також диференціалом першого порядку. Останню формулу можна записати ще так:

, (2).

Формула (2) дає змогу розглядати похідну як відношення диференціала функції до диференціала незалежної змінної.

Геометричний зміст диференціала: диференціал є лінійним наближенням до приросту функції.

Правила обчислення похідних і диференціалів.

На практиці функції диференціюють за допомогою ряду правил і формул.

Теорема: Якщо функції диференційовані в точці х, то сума, різниця, добуток і частка цих функцій (частка за умови, що ) також диференційовані в цій точці і справедливі такі формули:

Основні формули диференціювання функцій

.

.

.

.

.

.

.

.

.

.

.

.

.

Застосування поняття похідної в економіці.

Якщо на момент часу виробник виготовив одиниць продукції, то відношення , де – приріст випущеної продукції за час , називають середньою продуктивністю праці виробника за час , а границю

• продуктивністю праці виробника в момент часу (економічний зміст похідної).

При вивченні економічних процесів широко використовують обчислення похідних, які часто називають граничними значеннями функції.

В економіці звичайно користуються середніми величинами: обчислюють середню собівартість продукції, середню продуктивність праці і т. д., проте при вивченні виробничих процесів зустрічаємося з такою задачею: треба з’ясувати на яку величину зростуть витрати виробництва, якщо збільшити обсяг продукції, і, навпаки, на скільки зменшаться витрати виробництва, якщо скоротити обсяг продукції. У подібних задачах вимагається знайти границю відношення приросту ефекту до приросту витрат, або, як кажуть в економіці, граничний ефект. Нехай, наприклад, витрати виробництва однорідної продукції є функцією кількості продукції . Тому можна записати . Припустимо, що кількість продукції збільшилася на . Продукції відповідають витрати виробництва цієї продукції .

Отже, приросту кількості продукції відповідає приріст витрати виробництва продукції

.

Середній приріст витрат виробництва дорівнює приросту витрат виробництва, який припадає на одиницю приросту кількості продукції, тобто .

Для того, щоб визначити швидкість зміни витрат у момент, коли обсяг виробництва становить одиниць продукції, треба здійснити граничний перехід у виразі при прямуванні до нуля.

Границя

називається граничними витратами виробництва. Аналогічно, якщо ми позначимо через виручку від продажу одиниць товару, то границю

називатимемо граничною виручкою.

Нехай на проміжку задано функцію . Зафіксуємо точку і надамо їй приросту таким чином, щоб .

Означення: Процентним приростом незалежної змінної називається відносний приріст незалежної змінної , тобто відношення .

Позначимо процентний приріст аргументу через . Отже,

, (3)

Означення: Процентним приростом функції називається відносний приріст функції в точці , тобто відношення

.

Позначимо процентний приріст функції через . Отже,

, (4)

Складемо відношення:

, (5)

Співвідношення показує, у скільки разів відносний приріст функції більший за відносний приріст незалежної змінної. Припустимо, що функція є диференційованою на проміжку . Тоді, перейшовши у рівності (5) до границі за умови , дістанемо

, (6)

Означення: Границю відношення процентного приросту функції до процентного приросту незалежної змінної, коли , називають відносною похідною функції в точці .

Відносну похідну функції називають ще еластичністю функції і позначають символом . Отже,

, (7)

Перепишемо формулу (7) у вигляді

, (8)

Припустимо, що незалежна змінна зросла на . Це означає, що . Оскільки , то з формули (8) дістаємо

або в процентах .

Отже, еластичність функції в точці наближено дорівнює процентному приросту функції (підвищенню або зниженню), який відповідає приросту незалежної змінної на .

Маргінальними витратами називають гранично можливі витрати в умовах хоча би постійного відтворення виробництва відповідної продукції. Аналогічно визначають маргінальні доходи та прибуток. Якщо позначити через витрати, дохід та прибуток виробництва одиниць продукції, то кожна з цих величин є певною функцією кількості одиниць виробленої та проданої продукції. Тоді економічний зміст похідної формулюється так: похідні дорівнюють маргінальній вартості, доходу та прибутку відповідно.