Запитання для самоперевірки:

1. Що називається системою лінійних рівнянь?

2. Яка система лінійних рівнянь називається однорідною?

3. Яка система лінійних рівнянь називається сумісною?

4. Яка система лінійних рівнянь називається визначеною?

5. Що називається розв’язком системи лінійних рівнянь?

6. Як розв’язується система лінійних рівнянь методом Крамера?

7. У чому полягає метод розв’язування системи лінійних рівнянь методом оберненої матриці, на чому він грунтується?

8. Які перетворення матриці називаються еквівалентними?

9. Як розв’язується система лінійних рівнянь методом Гаусса?

Завдання для виконання:

Завдання 6. Розв’язати систему лінійних рівнянь: а) за формулами Крамера; б)методом оберненої матриці; в) методом Гаусса:

1)

2)

3)

4)

5)

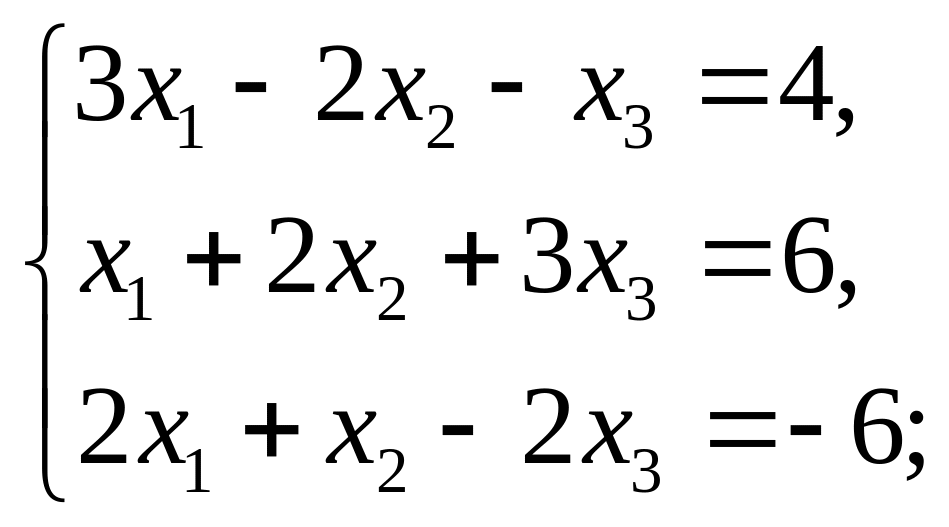
6)

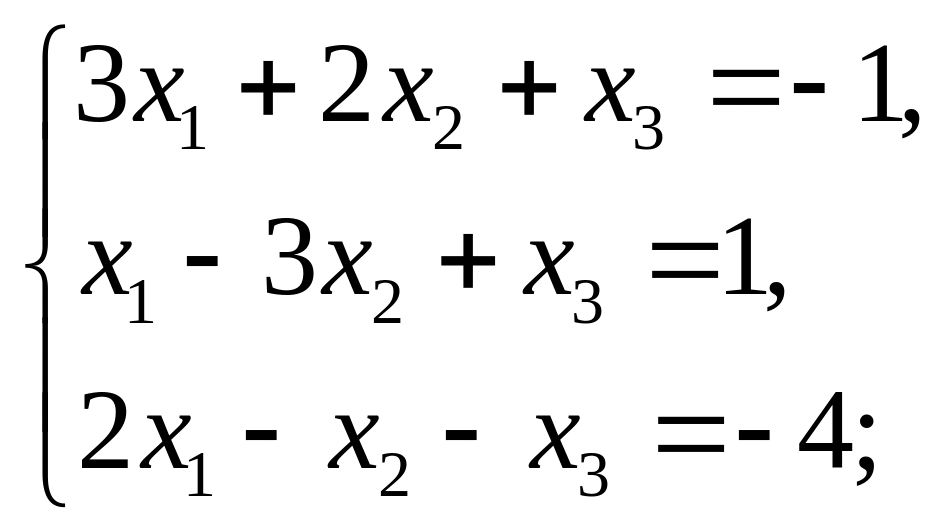
7)

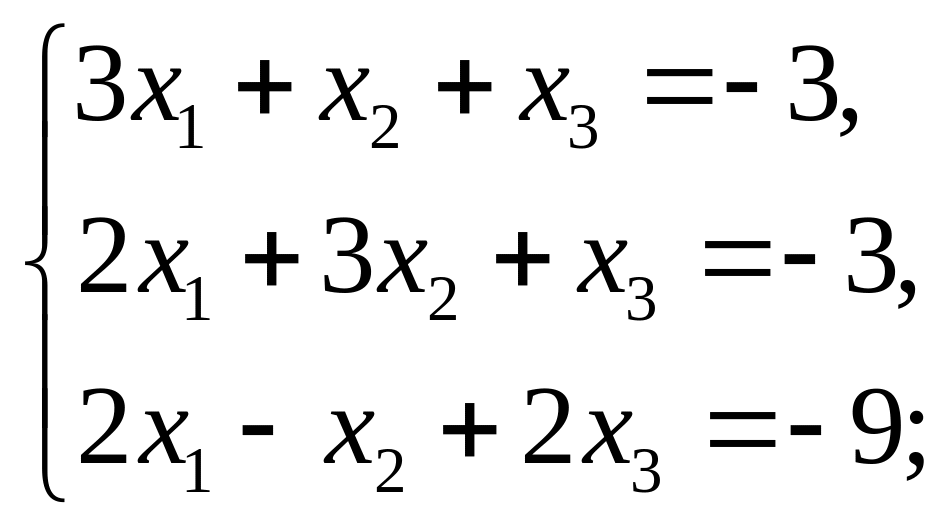
8)

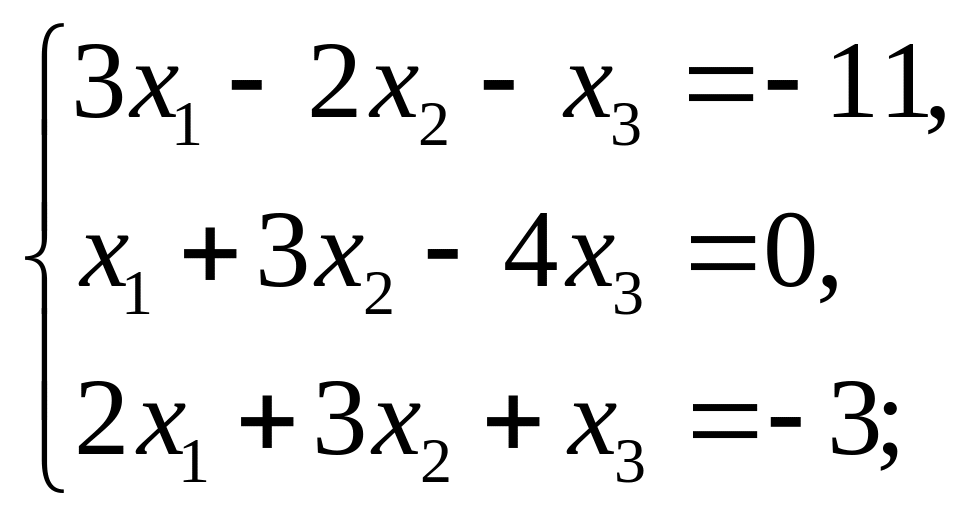
9)

10)

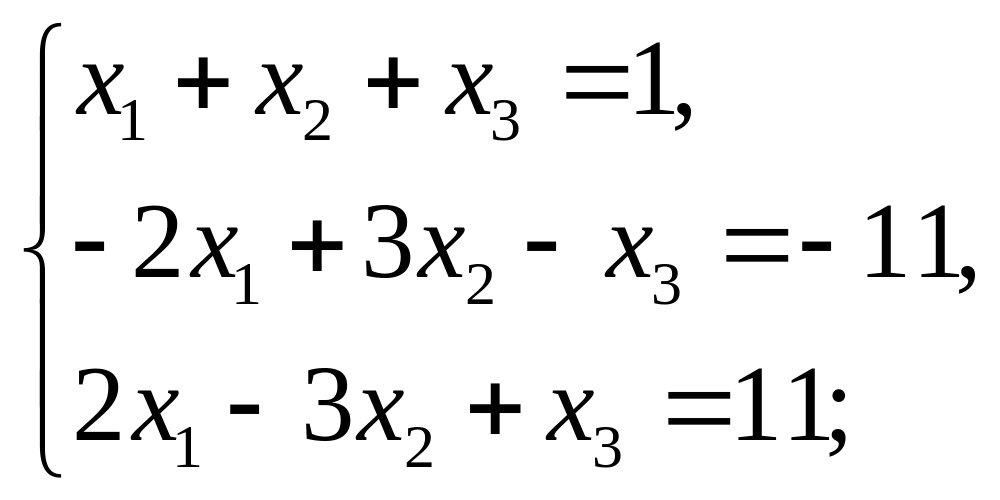
Література:

1. Соколенко О. І. Вища математика: Підручник. - К.: Видавничий центр „Академія", 2003. - 432 с. (Альма-матер).

2. Валєєв К.Г., Джалладова І.А. Вища математика: Навч. посібник: У 2-х ч. - К.: КНЕУ, 2001. - 546 с.

3. Дубовик В.П., Юрик І.І. Вища математика: Навч. посібник . - К.: А.С.К., 2001.-648 с.

4. Барковський В.В., Барковська Н.В. Вища математика для економістів. - Київ: ЦУЛ, 2002. - 400 с.

5. Л.І.Дюженкова, О.Ю.Дюженкова, Г.О.Михалін Вища математика. Приклади і задачі. - К: Видавничий центр „Академія" 2002 р.

Розділ 4

Тема: Лінійне програмування

Самостійна робота № 4

Питання 1. Постановка задач лінійного програмування.

Методичні вказівки:

Лінійне програмування є складовою частиною розділу математики, який вивчає методи знаходження умовного екстремуму функцій багатьох змінних і називається математичним програмуванням. В зв’язку з розвитком техніки, зростанням промислового виробництва все більшу роль почали відігравати задачі знаходження оптимальних розв’язків в різних сферах людської діяльності. З економічної точки зору задачі лінійного програмування пов’язані з пошуком способів найкращого розподілу і використання обмежених ресурсів (робоча сила, сировина, матеріали, засоби виробництва). При цьому шукають такий план (програму), який при певних обмеженнях на ресурси дає змогу досягнути, наприклад, найбільшого випуску продукції, найменших витрат виробництва тощо.

Основним інструментом при розв’язанні цих задач стало математичне моделювання – формальний опис явища, що вивчається і дослідження за допомогою математичного апарату. Мистецтво математичного моделювання полягає в тому, щоб врахувати як можна більше факторів по можливості простими засобами. Задача знаходження оптимального плану зводиться до математичної задачі – задачі на знаходження найбільшого чи найменшого значень функції при заданих обмеженнях. Функцію, найбільше або найменше значення якої вимагається знайти називають цільовою функцією. У задачах лінійного програмування цільова функція є лінійною функцією двох змінних.

У загальному вигляді задачу лінійного програмування можна записати так: знайти максимальне або мінімальне значення функції

при заданій системі обмежень

,

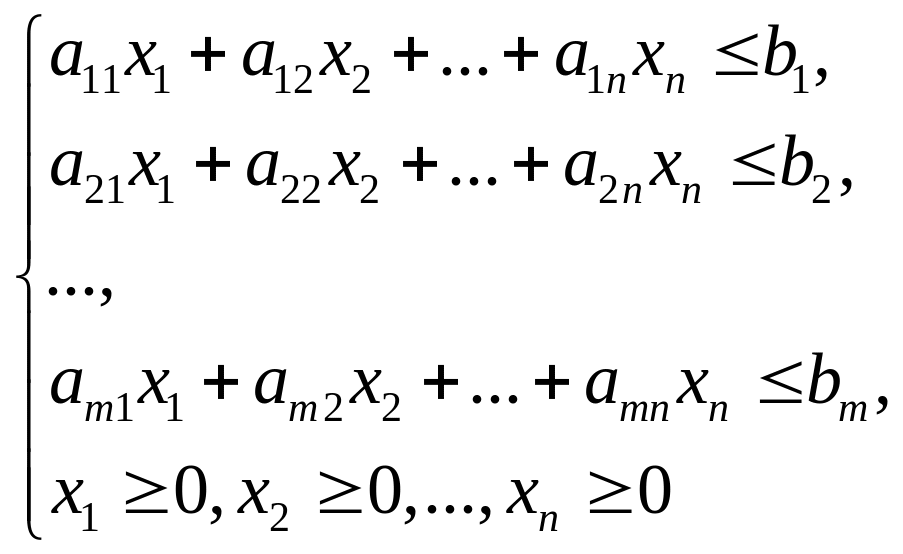– деякі числа, – змінні. Слід сказати, що у системі знаки нерівності можуть бути строгими, а можуть бути замінені знаками рівності.

Типовими задачами лінійного програмування є задача про використання ресурсів, задача раціонального харчування і транспортна задача.

Задача про використання ресурсів або інакше задача про максимальну рентабельність підприємства: як використати запаси сировини, що є на підприємстві, для виготовлення тієї чи іншої продукції, щоб дохід підприємства був найбільшим?

Приклад 1. Скласти математичну модель задачі лінійного програмування – задачі отримання максимального прибутку фірми: підприємство випускає продукцію двох видів А і Б. види сировини, їх запаси, норми витрат сировини на умовну одиницю продукції кожного виду занесені в таблицю:

Вид сировини	Запаси сировини	Норма витрат сировини на одиницю продукції кожного виду
		А	Б
І	450	2	3
ІІ	180	1	4
ІІІ	240	4	2

Дохід виробництва від реалізації умовної одиниці продукції виду А дорівнює 5 грн., а виду Б – 8 грн. Спланувати так випуск продукції, щоб дохід підприємства був найбільшим.

Розв’язування:

Позначимо через – кількість продукції виду А, – кількість продукції виду Б. Користуючись даними таблиці, складаємо систему обмежень:

Цільова функція матиме вигляд: .

Задача раціонального харчування полягає в наступному: із наявних продуктів потрібно скласти таку дієту, яка задовольняла б потреби людини в поживних речовинах (жирах, білках, вуглеводах, вітамінах і т.д.) і вимагала б найменших затрат.