1.7. Скорость создания информации дискретным источником без памяти

Существует достаточно большое количество моделей источников информации (сообщений). Особенности каждой конкретной модели рассматриваются при решении определенной задачи.

К наиболее простой модели источников относят дискретный источник без памяти, что позволяет доступно оценить его информационные способности.

Понятие «дискретный источник» является в большей мере условным и используется для простоты рассмотрения информационных свойств источников, так как любой непрерывный источник с некоторыми допущениями можно свести к дискретному источнику.

Источник без памяти – это источник, формирующий сообщения вне зависимости от ранее сформированных сообщений.

В источниках без памяти сообщения выдаются в некоторые моменты времени, определяемые самим источником, и не зависят от работы передающего устройства. В этом случае можно говорить о производительности источника, т. е. о среднем количестве информации, выдаваемом источником в единицу времени.

Если в среднем каждое элементарное сообщение занимает время t, то производительность источника будет равна

,

где Н(Х) – энтропия сообщения.

Следует заметить, что производительность источника зависит не только от количества элементов, составляющих сообщения, но и от корреляционных связей между элементами сообщений. Для того, чтобы более точно определить информационные характеристики источников сообщений, необходимо знать зависимость передаваемых сообщений друг от друга.

Задача. Определить скорость создания информации системой, которая описывается дискретной случайной величиной х со следующим рядом распределения: р(х₁) = р(х₂) = р(х₃) = р(х₄) = = 0,01; р(х₅) = 0,96, если система генерирует элемент сообщения за 0,1 с.

Решение. Найдем энтропию источника сообщений:

Н(Х) = – (4  0,01 log₂0,01 + 0,96 log₂0,96) = 0,322 бит.

Производительность источника составляет

С(Х) = 0,322 бит / 0,1 с = 3,22 бит/с.

Если же сообщения источника равновероятны:

р(х₁) = р(х₂) = р(х₃) = р(х₄) = р(х₅) = 0,2,

то энтропия источника равна примерно 2,322 бит, а производительность источника – 23,22 бит/с.

Задачи

1. Определить энтропию системы, которая описывается дискретной случайной величиной х со следующим рядом распределения: р (х₁) = = р (х₂) = р (х₃) = р (х₄) = р (х₅) = 0,2.

2. Какое количество информации приходится на букву алфавита, состоящего из 16 букв?

3. Определить энтропию сообщения из восьми букв, если общее число букв в алфавите равно 28 и все сообщения равновероятны.

4. Определить количество символов в алфавите, если появление сообщений равновероятно и энтропия сообщения из трех букв 21 бит.

5. Определить условную энтропию ансамбля двух источников, если р (х₁) = 0,4; р (х₂) = 0,2; р (х₃) = 0,4; р (у₁) = 0,36; р (у₂) = 0,26; р (у₃) = = 0,38. Матрица совместных вероятностей имеет вид

.

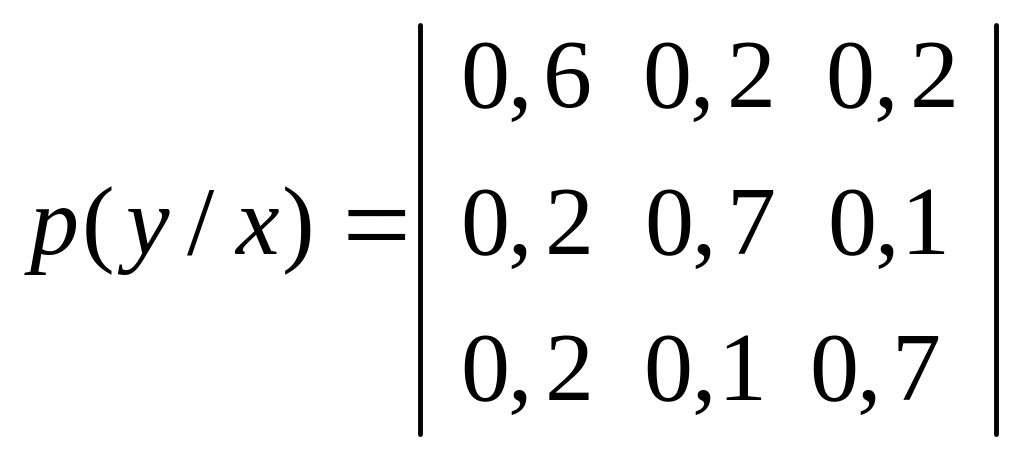Контрольные вопросы

1. Что называется информацией, сообщением, сигналом?

2. В каких единицах измеряется количество информации?

3. Что характеризует энтропия источника сообщений? Какова ее размерность?

4. Перечислите свойства энтропии.

5. Дайте определение взаимной энтропии, совместной энтропии.

6. В чем разница между взаимной и совместной энтропией?

7. Что является причиной избыточности сообщений?

8. Раскройте понятие «дискретный источник без памяти».

9. Как определить избыточность сообщений?

10. Как определить производительность источника сообщений?