2. Взаимная информация и взаимная энтропия

При передаче информации по каналу связи на передаваемый сигнал действуют помехи различного характера. Вследствие этого возникают различные ошибки. Например, при передаче бита «0» из 600 раз значение бита, равное «0», было принято 540 раз, «1» – 60 раз. Аналогично при передаче бита «1», из 400 раз значение бита, равное «1» было принято 320 раз, «0» – 80 раз. Как определить неопределенность возникновения комбинаций вида 1 – 0; 1 – 1; 0 – 0, 0 – 1?

Пусть (x₁ , x₂ , …, x_i , …, x_n) есть выборочное пространство X (ансамбль сообщений Х), характеризующее источник сообщений, а (y₁ , y₂ , …, y_j , …, y_n) есть выборочное пространство Y (ансамбль принятых сообщений Y), характеризующее приемник сообщений (рис. 1).

p (y₁ / x₁)

p (y₁ / x₃)

p (y₃ / x₁)

p (y_n / x₁)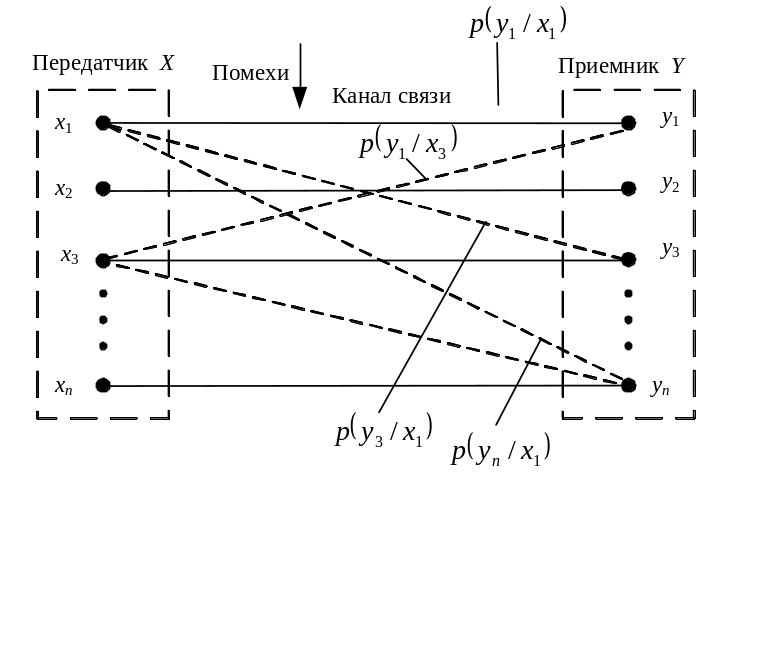

Рис. 1. К определению взаимной информации

При этом x_i есть i-й сигнал на входе канала, y_j есть j-й сигнал на его выходе. В идеальном канале без помех передача x_i однозначно определяет прием y_i. В реальных каналах передача информации неизменно сопровождается помехами, действие которых приводит к искажению передаваемых сообщений (переходу x_i к y_j). В этом случае взаимная энтропия представляет собой информацию о переданном сигнале x_i , содержащуюся в принятом сигнале y_j. Допустим, что искажения сообщений в канале связи не приводят к увеличению их общего числа.

Взаимосвязь переданных и принятых сигналов описывается вероятностями совместных событий вида p(x, y), а взаимосвязь выборочных пространств X и Y описывается матрицей вида

.

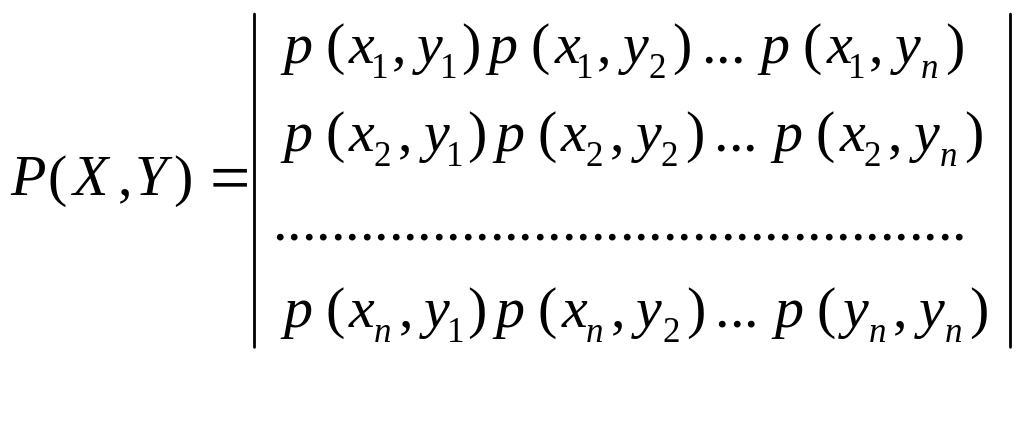При рассмотренных ограничениях матрица с вероятностных позиций описывает канал связи и носит название канальная матрица. Канальная матрица имеет число строк, равное числу столбцов.

Канальная матрица при условии известности ее элементов, используется для расчета энтропии источника H(X) и приемника H(Y) сообщений, а также взаимной информации и взаимной энтропии.

Под взаимной энтропией источника сообщений и приемника сообщений H(X / Y) понимается энтропия передаваемых сооб­ще­ний X при условии принятия сообщений Y. Аналогично трактуется понятие взаимная информация.

Взаимная информация и взаимная энтропия имеют свойства, аналогичные свойствам условной информации и условной энтропии, хотя по сути эти понятия полностью различны.

Для взаимной энтропии справедливо двойное неравенство

0  H(X / Y)  H(X).

При этом равенство H(X / Y) = 0 имеет место в том случае, когда, зная реализацию Y (конкретные принятые сообщения или сообщение), можно точно установить реализацию X (то что было сформировано источником сообщений). Другими словами, H(X / Y) = 0 в случае, если Y содержит полную информацию об X, а это возможно только в канале связи без помех.

Другой крайний случай, когда H(X / Y) = H(X), имеет место, если значение реализации Y не уменьшает неопределенности X, т. е. Y не содержит никакой информации об Х. Данный случай соответствует каналу с высоким уровнем помех, при передаче сообщений по которому полностью разрушается соответствие x_i и y_i.

В общем случае условная энтропия Н(X / Y) меньше безусловной Н(X) и знание реализации Y в среднем снижает первоначальную неопределенность Х.

Естественно назвать разность Н(X) – Н(X / Y) количеством информации, содержащимся в Y относительно Х. Информацию, содержащемся в Y относительно Х, называют также взаимной информацией между Х и Y и обозначают J(Y, X):

J(Y, X) = H(X) – H(X / Y).

Величина J(Y, X) показывает, сколько в среднем получают бит информации о переданном сообщении ансамбля Х, наблюдая принятое сообщение ансамбля Y.

Сформулируем основные свойства взаимной информации:

1. J(X, Y)  0, причем равенство имеет место тогда и только тогда, когда Х и Y независимы. Это следует из определения и неравенства 0  H(X / Y)   H(X).

2. J(X, Y) = J(Y, X), т.е. Y содержит столько же информации относительно Х, сколько Х содержит информации относительно Y. Поэтому можно также записать

J(X, Y) = H(Y) – H(Y / X).

3. J(X, Y)  H(X), причем равенство имеет место только в случае если по принятым сообщениям Y можно однозначно восстановить переданные сообщения Х.

Изменим незначительно трактовку вопроса. Пусть Х – ансамбль дискретных сообщений, а Y – ансамбль дискретных сигналов, в которые преобразуются сообщения Х. Тогда J(X, Y) = = H(X) в том и только в том случае, если преобразование Х  Y обратимо. При необратимом преобразовании J(X, Y) < H(X) и разность

H(X) – J(X,Y) = H(X / Y)

можно назвать потерей информации при преобразовании.

1.6. Избыточность сообщений

Энтропия сообщений при одинаковом количестве элементов (символов) может быть различной в зависимости от статистических характеристик сообщений. Энтропия максимальна, если элементы сообщения равновероятны и взаимно независимы. Если появление элементов сообщения не равновероятно, то энтропия уменьшается.

Еще меньшей будет энтропия при наличии коррелятивных связей между элементами сообщений. Сообщения, энтропия которых максимальна, являются оптимальными с точки зрения наибольшего количества передаваемой информации.

Мерой количественной оценки того, насколько данное реальное сообщение по своей энтропии отличается от соответствующего ему оптимального сообщения, является коэффициент сжатия

,

где H(X) – энтропия реального сообщения; H(X)_max – энтропия соответствующего ему оптимального сообщения.

Пусть неоптимальное и оптимальное сообщения характеризуются одинаковой общей энтропией. Тогда справедливо равенство

nH(X) = n H(X)_max,

где n – число элементов неоптимального сообщения; n – число элементов соответствующего ему оптимального сообщения.

Так как средняя на элемент энтропия оптимального сообщения максимальна, то число элементов неоптимального сообщения всегда будет больше числа элементов соответствующего ему оптимального сообщения.

Коэффициент сжатия можно выразить и через количество элементов сообщения:

.

Таким образом, реальные сообщения при одинаковой информативности обладают определенной избыточностью в элементах по сравнению с оптимальными сообщениями.

Мерой количественной оценки избыточности является коэффициент избыточности

.

Избыточность приводит к увеличению времени передачи сообщений, излишней загрузке канала связи. Однако не всегда нужно стремиться к тому, чтобы избыточность отсутствовала. Некоторая избыточность бывает полезной для обеспечения требуемой надежности систем, повышения помехоустойчивости передачи сообщений. Например, иногда практикуется повторная передача одного и того же сообщения с целью повышения достоверности его приема в условиях воздействия помех.

Задача. Определить избыточность системы, которая описывается дискретной случайной величиной х со следующим рядом распределения: р(х₁) = р(х₂) = р(х₃) = р(х₄) = 0,01; р(х₅) = 0,96.

Решение. Зная, что самой большой энтропией обладает система с равновероятным появлением элементов, находим оптимальную и реальную энтропии источника:

Н(Х)_max = log₂5 = 2,3219 бит;

Н(Х) = – (4  0,01 log₂0,01 + 0,96 log₂0,96) = 0,322 бит.

Используя формулу для коэффициента избыточности, находим:

К_и = 1 – (0,322/2,3219) = 1 – 0,1387 = 0,8613.

Таким образом, при равных энтропиях идеального и реального источников сообщения реального источника будут представлены бόльшим числом символов: .