1. Энтропия источника сообщений

В теории информации принят энтропийный подход к измерению количества информации. Понятие «энтропия» введено К. Ше­нноном в 1948 г.

Пусть сообщения можно передавать по каналу связи с помощью некоторого набора символов (например, букв, а вообще здесь подразумеваются любые символы, называемые алфавитом) Х, причем полное число символов в наборе равно m.

Будем полагать, что величины вероятностей появления любого из символов р_i , где i = 1, 2, …, m, априори известны.

Энтропией источника сообщений называют среднее (статистическое усреднение по всем возможным символам) значение количества информации, приходящееся на один символ алфавита (размерность энтропии бит/символ):

.

Энтропия характеризует неопределенность сообщения.

Определим среднее количество информации, передаваемое источником с алфавитом Х.

.

Несмотря на совпадение зависимостей, энтропия Н(Х) и количество информации I(X) принципиально различны. Энтропия Н(Х), выражающая среднюю неопределенность состояния источника сообщений, является объективной характеристикой источника сообщений и, если известны вероятности появления сообщений, может быть вычислена априори, т.е. до получения сообщения. Величина же I(X) определяется апостериорно, т.е. после получения сообщений. Н(Х) есть мера недостатка информации о состоянии отдельной системы. С поступлением информации о состоянии системы энтропия последней снижается.

Совпадение выражений для I(X) и Н(Х) свидетельствует лишь о том, что количество получаемой информации численно равно энтропии, которая имела место относительно источника сообщений.

В случае равной вероятности сообщений выражение для количества информации приводится к виду

,

где – количество передаваемых элементарных сообщений.

Выражение для энтропии в этом случае приобретает вид

.

В случае, если алфавит источника равен m, а сообщения составляются из набора символов n, то число возможных сообщений равно N = mⁿ. Тогда количество информации, которое может передавать источник (численно равно энтропии), равно (формула Хартли)

.

Анализируя рассмотренное, можно утверждать, что энтропия дискретных сообщений обладает следующими свойствами:

1. Энтропия есть величина вещественная, ограниченная и неотрицательная. Это свойство следует из расчетной формулы, если учесть, что вероятности p_i есть величины неотрицательные, заключенные в промежутке 0  p_i  1.

2. Энтропия детерминированных сообщений равна нулю. Действительно, если заранее известно, какое будет событие, например х₁ , то вероятность этого события равна единице, а остальных – нулю, т.е. р₁ = 1; р₂ = р₃ = … = р_n= 0. Подставляя эти значения в формулу, получим

.

Первый член равен нулю, поскольку log_a 1 = 0. Остальные члены также обращаются в нуль при p_i  0.

3. Энтропия максимальна, если все сообщения равновероятны. Проиллюстрируем рассмотренный материал.

Задача. Определить энтропию системы, которая описывается дискретной случайной величиной х со следующим рядом распределения: р₁ = 0,01; р₂ = 0,01; р₃ = 0,01; р₄ = 0,01; р₅ = 0,96.

Решение. Используя выражение для определения энтропии дискретного распределения, получим

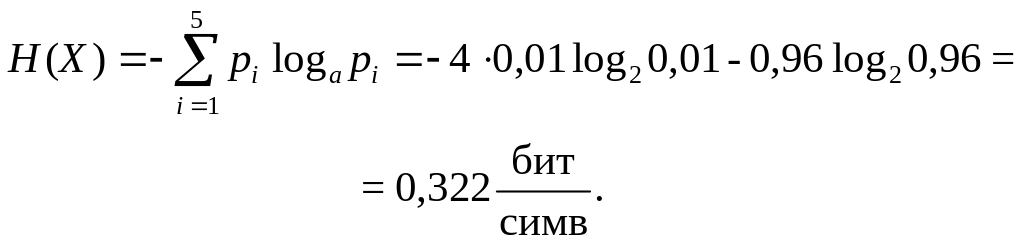
Определить энтропию системы, которая описывается дискретной случайной величиной х со следующим рядом распределения: р₁ = р₂ = р₃ = р₄ = р₅ = 0,2.

Решение.

Задача. Определить энтропию сообщения из пяти букв, если общее число букв в алфавите равно 32 и появление всех букв в сообщении равновероятно.

Решение. Общее число пятибуквенных сообщений n = 32⁵. Используя выражение для определения энтропии равновероятных сообщений, получим

.

Используя свойства энтропии, еще раз поясним смысл понятия.

Энтропия – это средняя информативность источника на один символ, определяющая «непредсказуемость» или «неожиданность» передаваемых источником сообщений. Полностью детерминированный источник, вырабатывающий одну полностью известную последовательность символов, обладает нулевой информативностью. Наоборот, полностью хаотический источник, выдающий независимые и равновероятные символы, обладает наибольшей информативностью.

Для большей доступности понятия энтропии специалисты часто приводят пример с обезьяной, сидящей за клавиатурой компьютера. Поскольку она не знает грамоты, но умеет ударять по клавишам, то набираемый ею текст окажется сообщением с взаимно независимыми и равновероятными символами. Поэтому «обезьяний» текст будет обладать наибольшей энтропией.