2. Пропускная способность непрерывного канала связи

Если теоретически предположить, что в канале связи отсутствуют всякие шумы, то задача о пропускной способности теряет смысл – любой объем информации можно было бы передать достаточно быстро и с высокой верно­стью.

Реальное наличие в канале связи шумов различного происхождения резко усложняет проблему. Интенсивность информационного потока жестко связа­на с шириной полосы частот, занимаемых сигналом, а также величиной от­ношения сигнал/шум на входе приемника. Совершенно очевиден тот факт, что канал связи тем совершеннее, чем шире полоса частот и чем больше поддерживается от­ношение сигнал/шум на выходе приемного устройства.

Количественные оценки, дающие возможность решить данную проблему, были получены впервые К. Шенноном в его классической работе по теории связи.

Упрощенно рассуждения К. Шеннона сводились к следующему. Пусть имеется некоторый канал системы связи с шириной полосы пропускания F_к. Предположим, что Р_с – средняя мощность полезного сигнала на входе при­емника, а в канале присутствует белый гауссовский шум, мощность которого на входе приемника составляет величину Р_ш.

Для надежного различения двух отсчетов сигнала необходимо, чтобы данные, по­лучаемые при взятии отсчетов, отличались друг от друга на достаточную ве­личину, например не менее чем на среднеквадратическое отклонение, обу­словленное шумом. Поскольку дисперсии стационарных случайных процес­сов прямо пропорциональны их мощностям, число полностью «различимых» значений сигналов при взятии каждого отсчета соста­вит

.

Положим, что длительность передаваемой информации составляет Т_с се­кунд. Из теоремы Котельникова, определяющей, что отсчеты сигналов должны браться не реже, чем через интервал времени Δt = 1/ 2F_к , следует: за время длительности передаваемого сообщения Т_с может быть взято не менее 2T_с F_к отсчетных значений ( ). Тогда общее число различных сигналов, которые могут быть по­строены описанным способом, равно

.

Поскольку все сигналы равновероятны, то вероятность выбора одного кон­кретного сигнала равна P_i = 1/М. Очевидно, что число битов информации, кото­рое можно безошибочно передать за время Т_с , при этом составит

.

Максимальная скорость передачи информации (бит/с), достигаемая при этом, является пропускной способностью канала и равна

.

Это соотношение известно как формула Шеннона для пропускной способно­сти канала аналоговой системы связи с ограниченной полосой частот и ограни­ченной средней мощностью сигнала при наличии белого нормального шума.

Характер зависимости С = f (F_к) представлен на рис. 18.

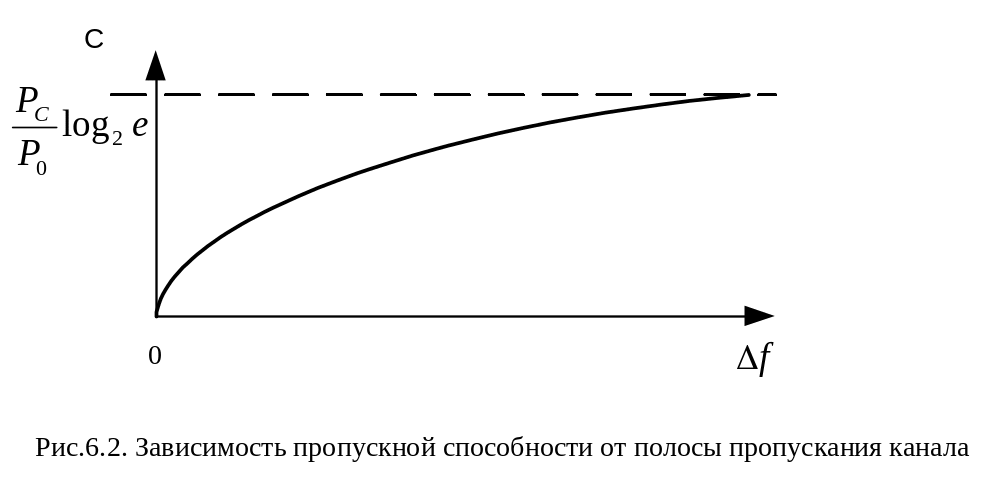
Рис. 18. Зависимость пропускной способности

от полосы пропускания канала

Формула Шеннона является важным инструментом при проектировании раз­нообразных каналов связи.

2. Пути повышения пропускной способности непрерывных каналов связи

Анализ формулы Шеннона показывает, что существуют два пути повышения пропускной способности канала связи:

- за счет расширения полосы частот канала;

- за счет повышения отношения сигнал/шум.

Однако эти пути не равноценны. Если F_к = const, a отношение сигнал/шум Р_с / Р_ш возрастает, то пропускная способность С также будет увеличиваться, но ее рост оказывается весьма медленным, посколь­ку подчиняется логарифмическому закону.

При фиксированном же значении отношения сигнал/шум и увеличении полосы пропускания канала F_к пропускная способность возрастает, как следует из формулы, линейно, однако можно показать, что в полосе пропус­кания не заключены неограниченные возможности ее увеличения.

Покажем, что зависимость пропускной способности канала от F_к при постоянной мощности сигнала нелинейная. Заметим, что мощность помехи также зависит от ширины частотного спектра. Энергетический спектр белого шума равномерен, поэтому его мощность можно представить в виде

P_ = P₀ F_к ,

где P₀ – мощность помехи, приходящаяся на полосу в 1 Гц (спектральная плотность мощности помехи).

Подставив формулу для мощности помехи в выражение для пропускной способности, получим выражение, определяющее действительный характер зависимости пропускной способности канала от ширины его полосы пропускания:

.

Из произведенного анализа можно заключить, что нет смысла сильно увеличивать полосу пропускания канала, так как по мере расширения полосы пропускания рост пропускной способности канала замедляется и в пределе при F_к   пропускная способность приближается к постоянной величине. Имеет смысл увеличивать полосу пропускания примерно до значения, равного отношению .

Пропускная способность может быть увеличена за счет увеличения отношения , но при этом потребуется значительное увеличение мощности передатчика.

Определим предел, к которому стремится пропускная способность канала при неограниченном увеличении его полосы пропускания:

.

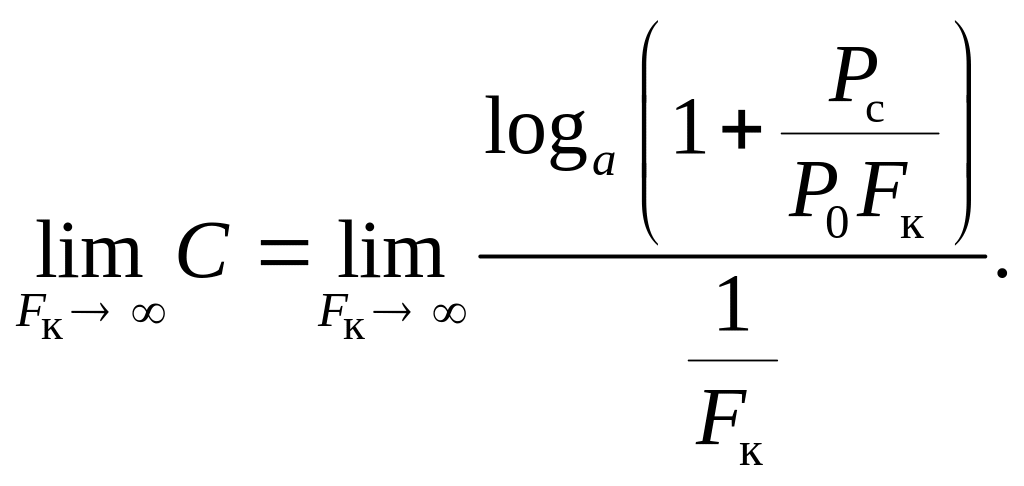Введя значение , получим

Раскрывая неопределенность, используя второй замечательный предел, получим предельное значение пропускной способности канала:

Из полученного соотношения видно, что максимальное значение, к которому стремится пропускная способность канала с ростом его ширины полосы пропускания, пропорционально отношению средней мощности сигнала к спектральной плотности мощности помехи.

Для непрерывного канала с помехами Шенноном сформулирована следующая теорема:

Если энтропия источника непрерывных сообщений, определяющая количество информации, вырабатываемое в единицу времени при заданной оценке g верности воспроизведения, сколь угодно близка к пропускной способности канала, т.е. справедливо соотношение

,

где  – как угодно мало, то существует метод передачи, при котором все сообщения, вырабатываемые источником, могут быть переданы, а верность воспроизведения при этом как угодно близка к g.

Обратное утверждение этой теоремы говорит о том, что такая передача невозможна, если

Теорема позволяет находить предельно достижимую эффективность непрерывных каналов.