Рекуррентные коды. Кодирование с перемежением
Принцип построения рекуррентных (сверточных) кодов
При использовании блочных корректирующих кодов одной из основных проблем считается проблема сложности кодера (декодера). Как правило, сложность кодера растет с увеличением длины кодовой комбинации экспоненциально, реже – линейно. С другой стороны, с увеличением длины кодовой комбинации уменьшается вероятность ошибки декодирования.
Метод кодирования-декодирования считается эффективным, если с ростом числа символов в кодовой комбинации вероятность ошибки декодирования Род уменьшается асимптотически экспоненциально, а сложность кодера растет линейно.
Кроме функции надежности и сложности кодера характеристикой метода кодирования – декодирования является трудоемкость декодирования, под которой понимают число элементарных операций, выполняемых декодером.
В настоящее время для блочных реализуемых кодов трудоемкость декодирования является степенной функцией длины кодовой комбинации, а вероятность ошибки декодирования уменьшается практически линейно. Поэтому блочные, в том числе и циклические коды, используются при малых длинах кодовых комбинаций.
Блочные коды недостаточно согласуются с последовательной природой источника, особенно [при использовании современных цифровых методов передачи непрерывных аналоговых сообщений (при импульсно–кодовой модуляции (ИКМ), дифференциальной импульсно–кодовой модуляции (ДИКМ) и дельта–модуляции (ДМ)].
Рекуррентные и сверточные (частный случай рекуррентных) коды в большей степени удовлетворяют цифровым методам передачи непрерывных сообщений.
Основная идея рекуррентного кодирования заключается в том, что кодер не имеет буфера и каждый информационный символ сразу же после поступления в кодер участвует в формировании кодовых символов, выдаваемых в канал.
Выходные кодовые символы bi1 , bi2 , …, bin формируются с помощью рекуррентного соотношения из V символов сообщения аi1 , аi2 ,…, аiq, поступивших в данный такт и в предшествующие такты (отсюда название – рекуррентный код). При этом каждый выходной кодовый символ зависит от q последних поступлений в кодер информационных символов до данного момента. Величина V называется длиной кодового ограничения. Она показывает, на какое максимальное число кодовых символов влияет данный информационный символ, и играет ту же роль, что и длина блочного кода. Отношение q/n = R называется скоростью кода, где q – количество символов входного сообщения; n - количество символов выходного сообщения, сформированных на основе q входных символов. Обычно q и n - взаимно простые числа.
Выходные символы можно рассматривать как результат свертки импульсной характеристики кодера с информационной последовательностью (отсюда название – сверточный код).
Типовые параметры сверточного кода: q, n = 1, 2, …, 8; R = = q / n = 1/4 …7/8; V = 3 … 10.
Рассмотрим общие принципы построения рекуррентных кодов на примере сверточных кодов.
На рис. 14 приведены схемы простейших кодеров, формирующих разделимый (а) и неразделимый (б) сверточные коды. Основными элементами сверточного кодера являются регистр сдвига, сумматоры по модулю 2, коммутатор.
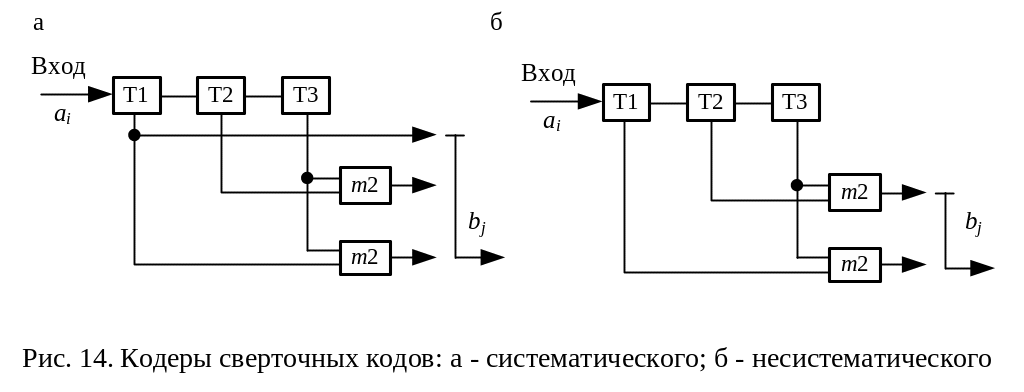
Рис. 14. Кодеры сверточных кодов:
а - систематического; б - несистематического
Видно, что алгоритм формирования выходной кодовой последовательности определяется функциональными связями в кодере.
В кодере (рис. 14, а) в канал, наряду с проверочными символами, формируемыми в сумматорах, передаются информационные символы (1-й контакт коммутатора). Кодер, имеющий такую связь, называется систематическим, а код - разделимым, так как выходную кодовую последовательность можно разделить на последовательность информационных и последовательность проверочных символов.
Кодер (рис. 14, б) не имеет такой связи. Он называется несистематическим и формирует неразделимый сверточный код. На практике обычно используются несистематические сверточные коды.
Можно заметить, что сигнал на выходе i-го сумматора образуется путем свертки кодируемой информационной и порождающей (связи кодера) кодовой последовательности. Поэтому код и называется сверточным.
Различают прозрачные и непрозрачные сверточные коды. Прозрачный сверточный код инвариантен к операции инвертирования кода: если значения символов на входе кодера поменять на противоположные, то выходная последовательность также инвертируется. У таких кодов неопределенность знака последовательности можно устранить после декодирования. Указанное свойство прозрачных кодов важно для систем передачи информации, которым свойственно явление обратной работы (инверсный прием кодовой последовательности).
Для непрозрачных сверточных кодов неопределенность знака кодовой последовательности необходимо устранять до сверточного декодирования, что приводит к увеличению вероятности ошибки.
Длина кодовых ограничений V и конкретный выбор связей в кодере определяют корректирующую способность кода.
Сверточный код обозначается (R, V)-код, т.е. код со скоростью R и длиной кодового ограничения V.
Для построения сверточного кодера необходимо указать число сумматоров и связи с каждым из сумматоров.
Выбор способа представления кода зависит от способа решаемой задачи и выбранного метода декодирования.
Достоинством несистематических сверточных кодов является лучшая корректирующая способность (при прочих равных условиях). Вместе с тем несистематические коды могут быть катастрофическими, когда конечное число ошибок, происшедших в канале связи, приводит к бесконечному числу выходных ошибок.
Систематические коды таким недостатком не обладают.
Задачей выбора структуры кодера является выбор таких связей в кодере, чтобы получить некатастрофический код с наилучшей корректирующей способностью.