3. Структурная схема кодера циклического кода

На рис. 12 приведена схема декодера циклического кода (7, 4) с порождающим полиномом . Код имеет кодовое расстояние, равное 3, что позволяет исправлять однократные ошибки.

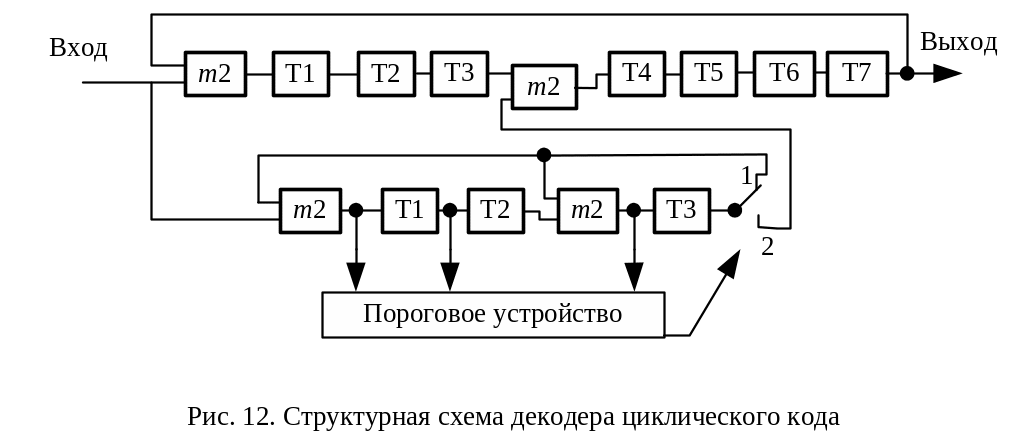
Рис. 12. Структурная схема декодера циклического кода

Принятая кодовая комбинация одновременно поступает в буферный регистр сдвига, служащий для запоминания кодовой комбинации и для ее циклического сдвига, и на устройство деления на порождающий многочлен для вычисления синдрома (вес остатком от деления).

В исходном состоянии ключ находится в состоянии 1. После семи тактов буферный регистр оказывается загруженным, а в регистре устройства деления будет вычислен синдром. Если вес синдрома больше единицы, то декодер начинает производить циклические сдвиги кодовой комбинации в буферном регистре при отсутствии новой кодовой комбинации на входе и одновременно вычислять синдромы. Если на каком-то шаге вес синдрома равен единице, то пороговое устройство переключает ключ в положение 2, при этом обратные связи в регистре разрываются.

При последующих тактах ошибки исправляются путем подачи содержимого регистра деления на вход сумматора по модулю 2, включенного в буферный режим. После семи тактов работы декодера в автономном режиме исправленная кодовая комбинация в буферном регистре возвращается в исходное положение (информационные символы будут занимать старшие разряды).

Кроме рассмотренного, существуют более универсальные методы декодирования циклических кодов.

К циклическим кодам относятся коды Хэмминга, Боуза – Чоудхури – Хоквингема (БЧХ) и др.

4.5.4. Мажоритарное декодирование

Наряду с рассмотренными циклическими кодами существуют коды, обладающие более худшей корректирующей способностью, но простые в реализации. Такие коды допускают иной алгоритм декодирования, так называемое мажоритарное декодирование.

Оно основано на возможности для некоторых циклических кодов выразить каждый информационный символ с помощью q различных линейных соотношений. Решение о значимости символа принимается по большинству значений, даваемых каждым отдельным соотношением.

Для исправления всех ошибок кратности t_и включительно необходимо иметь 2 t_и +1 соотношение.

Рассмотрим более подробно принцип мажоритарного декодирования на примере кода (7, 3) порождающим многочленом и проверочной матрицей (b₁ – b₇ – принятая кодовая комбинация):

.

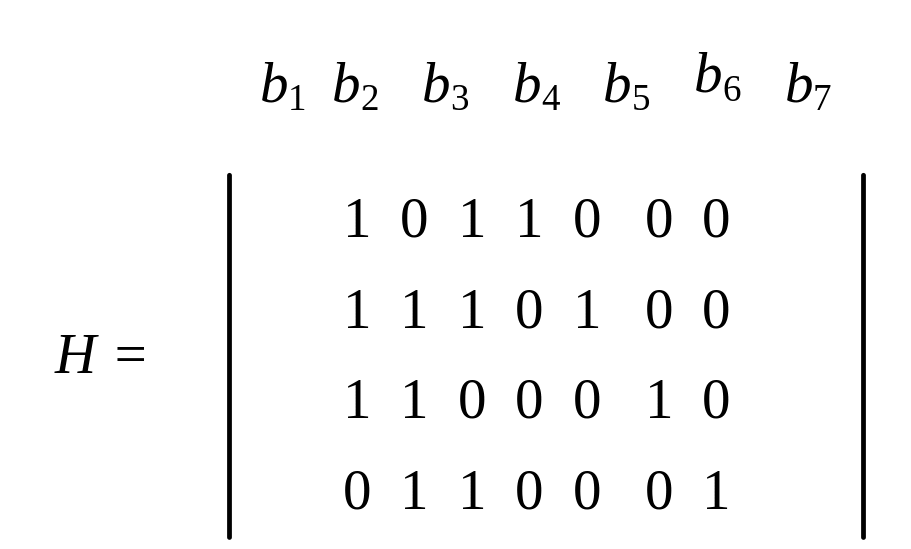
Данный код является циклическим, имеет кодовое расстояние, равное 4.

Из проверочной матрицы можно записать:

b₄ = b₁ b_{3 ,} откуда ;

, откуда ;

, откуда .

Складывая вторую и четвертую строку, имеем: . Сложим второе и четвертое уравнение и прибавим к ним тривиальное равенство b₁ = b₁. После преобразований относительно b₁ получим:

;

;

;

b₁ = b_1.

Таким образом, у декодера имеется четыре разных способа вычислить первый информационный символ b₁. Система уравнений образует систему раздельных проверок , позволяющих устранять одну ошибку.

При отсутствии ошибки все проверочные уравнения дают один и тот же результат. При наличии одной ошибки три уравнения дадут правильный результат, а одно – неправильный. Принимая решение по большинству, декодер выдает правильный символ b₁.

Если ошибочно принято два символа, то декодер выдает сигнал отказа от декодирования.

На рис. 13 представлен вариант мажоритарного декодера. На его выходе формируется символ 1, если на большинстве его выходов появилась единица. В противном случае формируется 0.

Рис. 13. Декодер циклического мажоритарного кода

Простота представленной схемы обусловлена тем, что каждый символ кодовой комбинации участвует в одном проверочном соотношении. Код, для которого выполняется это условие, называется кодом с раздельными проверками.

Следует отметить, что мажоритарное декодирование возможно только для отдельных циклических кодов, например кода Хемминга.

4.6. Модификации циклических кодов

При использовании кодирования в системах связи часто оказывается, что на длину кодового блока n или на число информационных символов k налагаются некоторые ограничения, в результате которых значения этих параметров должны отличаться от значений, наиболее предпочтительных при проектировании. В таких случаях код можно видоизменить, чтобы удовлетворить заданным ограничениям.

Всего известно шесть модификаций кодов:

- коды увеличенной длины путем ввода (добавления) информационных или проверочных символов;

- коды уменьшенной длины путем выбрасывания информационных или проверочных символов;

- коды с увеличенным или уменьшенным числом кодовых слов.

Покажем, как проводятся эти видоизменения на примере кода Хемминга (7, 4). Код может быть расширен путем добавления проверочных символов. Дополнительные проверочные символы выбираются так, чтобы они улучшали весовую структуру кода.

Обычным случаем такой модификации является введение одной общей проверки на четность. Значение соответствующего проверочного символа равно остатку от деления первоначального кодового слова на многочлен (x – 1). При этом вес каждого кодового слова становится четным.

Кодирование информационной кодовой комбинации (например, 1010) циклическим кодом Хемминга (7, 4) с кодовым расстоянием d_min = 3, образующим полиномом G(x) = 1 + х + х³, производится на основании известных правил.

Для расширения кодового слова [получения кода (8, 4)] вводится обобщенная проверка на четность, определяющая, что дополнительный проверочный символ является остатком от деления исходной кодовой комбинации 1010 на многочлен (x – 1) (код 11): последний символ равен нулю. Можно показать, что образованное кодовое слово 10100110 кода (8, 4) при циклическом сдвиге делится на образующий полином без остатка, а кодовое расстояние такого кода равно 4.

Заметим, что обобщенная проверка на четность может быть применена для любого кода с нечетным кодовым расстоянием, при этом кодовое расстояние увеличивается на 1.

Код может быть уменьшен по длине (выколот) путем удаления некоторых проверочных символов. Эта процедура обратна процедуре расширения кода. При выбрасывании отдельного проверочного символа необходимо, чтобы кодовое расстояние не изменилось, так как при некорректном выкалывании кодовое расстояние может уменьшиться на 1.

Операция выбрасывания выполняется путем отбрасывания некоторых кодовых слов. Для циклического кода эта процедура выполняется путем умножения порождающего полинома на дополнительный сомножитель (хⁿ - 1). Наиболее часто встречается код с выбрасыванием, порожденный полиномом G(х)/(х - 1). Кодовыми словами этого кода являются все слова четного веса исходного кода. Так, в результате выбрасывания из (7, 4) кода Хемминга проверочного символа получается (7, 3) код с минимальным кодовым расстоянием, равным 4, порожденный многочленом G(x) = (1 + х + х³ ) · (1 + х).

Код может быть пополнен путем добавления новых кодовых слов. Циклический код, порожденный многочленом G(х), может быть дополнен до кода той же длины, порождающий многочлен которого является некоторым множителем G(х). Если, например, G(х) содержит сомножитель (х - 1), то пополненный код будет порождаться многочленом G(х) / (х - 1).

Код может быть удлинен путем добавления дополнительных символов. Если начать с циклического кода, для которого G(х) делится на (х - 1), то удлинение этого кода проводится в два этапа. Сначала код надо пополнить до кода, порожденного полиномом G(х) / (х - 1), что соответствует добавлению к коду слова, состоящего только из единиц. Далее полученный код нужно расширить, добавив общую проверку на четность. В большинстве случаев эта процедура не приводит к уменьшению кодового расстояния.

Код может быть укорочен путем удаления некоторых информационных символов. Для циклического кода такую процедуру проводят, полагая лишние информационные символы каждого кодового слова равными нулю.