1. Принцип построения циклического кода

Циклические коды, как и коды с обобщенной проверкой на четность, относятся к линейным блочным систематическим кодам. Основное свойство циклических кодов состоит в том, что любая циклическая перестановка (сдвиг влево или вправо, при этом младший разряд кодовой последовательности становится старшим, и наоборот) приводит к формированию нового кодового слова, принадлежащего этому коду.

Один из вариантов описания циклических кодов предусматривает использование полиномов степени (n - 1), у которых элементы кодовых слов (а₁, а₂, …, а_{n - 1}) являются коэффициентами многочлена:

.

Например, х⁵ + х³ +х²+1 соответствует коду 1 0 1 1 0 1. В этой связи циклический код также называют полиномиальным.

При таком подходе полиномиальный код описывается как множество всех многочленов степени не больше (n - 1), у которых общим множителем является фиксированный полином G(х) степени не меньше (n – k).

Многочлен G(х) называется порождающим полиномом и используется при построении кода.

Циклические коды, как и любые блочные линейные коды, могут быть описаны с помощью порождающей и проверочной матриц.

Порождающая матрица получается из единичной транспонированной матрицы Е^Т путем приписывания к ней справа матрицы дополнений R:

.

Матрица дополнений строится следующим образом.

Каждая строка единичной матрицы Е размером k × k умножается на полином х ^{n - k} (по правилам умножения сдвигается влево на n - k разрядов и дополняется n - k нулями).

Полученные таким образом строки новой матрицы размером n × k делятся каждая на образующий полином. В результате деления получаются k остатков от деления, каждый из которых представляет собой строку матрицы дополнений.

Порождающая матрица дает возможность получить первые k комбинаций кода. Остальные кодовые комбинации получаются в результате суммирования по модулю 2 строк производящей матрицы во всех возможных комбинациях. Последняя кодовая комбинация является нулевой.

Следует отметить, что такой подход позволяет сформировать k - 1 вариант кода, каждый из которых отличается длиной n, количеством информационных символов k и скоростью передачи информации при одинаковых корректирующих возможностях. Эти варианты так называемых укороченных циклических кодов получаются путем вычеркивания некоторого количества последних строк и такого же количества левых столбцов в порождающей матрице. При этом число проверочных символов в каждом укороченном коде остается неизменным.

Рассмотрим на примере построение порождающей матрицы полного и укороченного циклического кода для n = 15 и k = 11. Число проверочных символов r = 4.

Возьмем первую строку матрицы Е вида 10000000000 и сдвигаем влево на 4 разряда (приписываем 4 нуля).

Выбираем порождающий многочлен (как правило, полином выбирается из таблицы неприводимых примитивных полиномов, см. приложение), например G(x) = х⁴ + х³ + 1, которому соответствует комбинация 11001.

Выбор порождающего полинома зависит от предназначения кода. Если код предназначен для исправления независимых ошибок, то полином должен обеспечивать заданное кодовое расстояние.

Степень образующего полинома должна быть не меньше числа проверочных символов r, а сам полином должен входить в качестве сомножителя разложения двучлена х ^п + 1.

Делим полученную 15-разрядную кодовую комбинацию на порождающий многочлен и получаем остаток от деления (см. рис. 8).

Рис. 8. Деление кодовой комбинации

на порождающий полином

Аналогичные действия проводим с оставшимися строками матрицы Е, получая остатки: 1010, 0011, 1101, 0101, 1110, 0111, 1111, 1011, 1001, 1000.

Производящую матрицу запишем в виде совокупности Е^Т и R, составленной из остатков:

G_{15, 11} =

.

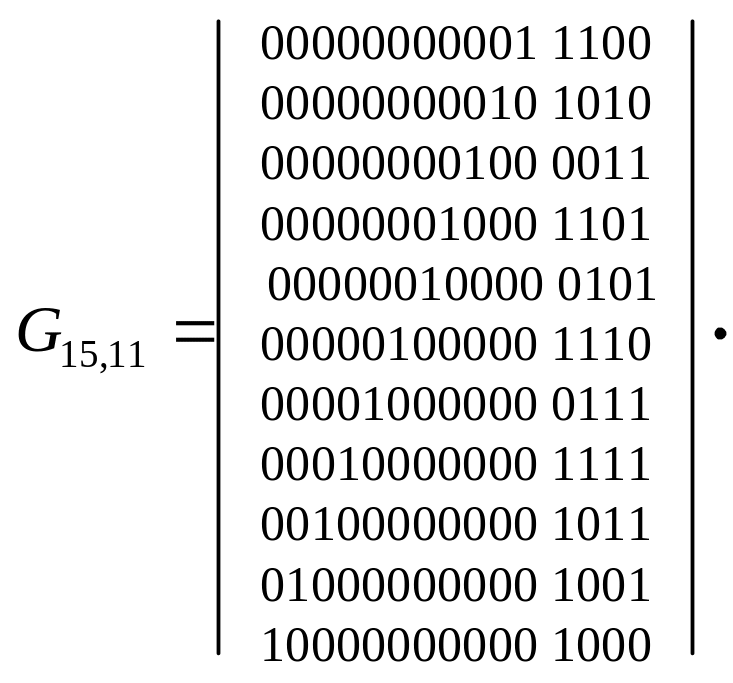
Для получения производящей матрицы укороченного циклического кода производится вычеркивание левых столбцов и нижних строк.

Путем линейного комбинирования строк порождающих матриц можно получить все остальные кодовые слова данных кодов.

Процесс кодирования в циклических кодах сводится к определению числа проверочных символов r по известному числу информационных символов, а также к выбору порождающего полинома. Обычно r (число корректирующих символов) либо выбирается по специальным таблицам, либо обосновывается путем расчета.

Р. Боуз и Б. Чоудхури доказали, что для любых целых положительных m (порядок образующего полинома) и t_и (число ошибок, подлежащих исправлению) существует циклический код значимости

n = 2 ^m – 1

с кодовым расстоянием

d_min ≥ 2t_и + 1.

При этом число проверочных символов не превышает m t_и , т. е. r ≤ m t_и. Такой код гарантированно исправляет ошибки кратности t_и и менее или обнаруживает ошибки кратности 2 t_и .

Корректирующая способность кода тем выше, чем больше остатков может быть образовано при делении многочлена сообщения на образующий полином. Наибольшее число остатков дают неприводимые примитивные полиномы степени m (2^m – 1 остатков), которые и используются в качестве образующих.

Основными операциями при кодировании сообщения А(х) являются: умножение многочлена сообщения А(х) на многочлен х ^r , нахождение остатка от деления А(х)·х ^r на G(х), а также сложение остатка по модулю 2 с многочленом А(х)х ^r :

.

Отметим, что образующий полином структурно входит в код.

4.5.2. Структурная схема кодера циклического кода

Операции, выполняемые при кодировании и декодировании циклического кода, легко реализуются линейными целями на базе сдвигающих регистров.

На рис. 9. в качестве примера приведена схема умножения многочлена b(х) степени п = 6 на многочлен f (х) = х³ + х + 1 по модулю х⁷+1, а также схема деления многочлена b(х) на многочлен f (х) = х³ + х² + 1.

Принцип работы данных схем будет понятен, если вспомнить правила умножения и деления двоичных чисел (полиномов). b(х) f (х).

Умножение на полином третьей степени (х³) соответствует сдвигу исходного кодового слова влево на три позиции (приписыванию трех нулей). В схемном исполнении та же операция выполняется подачей умножаемой последовательности на вход четвертого триггера регистра. При умножении исходного полинома на х умножаемая последовательность подается на вход второго триггера регистра и т. д. (см. рис. 9, а). Таким образом, полином-множитель в схеме выполняется в виде набора связей, а полином -множимое является кодовой последовательностью, потактно подаваемой в сдвигающий регистр. Сумматоры по модулю 2 выполняют функции поразрядного суммирования. После 7 тактов в регистре останется результат умножения b(х) и f (х) по модулю х⁷+ 1 (семиразрядный регистр).

Рис. 9. Схемы умножения (а) и деления (б) многочленов (частный случай)

Деление на полином второй степени соответствует сдвигу вправо исходного кодового слова. В схеме рис. 9 на третьем такте три младших разряда заполнят сдвигающий регистр. На четвертом и последующих тактах умножаемая последовательность подается на сумматоры по модулю 2 с задержкой в 3 (выход х³) и 2 (выход х²) такта, а также без задержки (выход 1). В регистрах Т1 – Т3 по завершении 6 тактов останется остаток от деления. Таким образом, полином-делитель выполняется в схеме в виде набора функциональных связей.

На основе приведенных схем умножения и деления строятся кодирующие и декодирующие устройства циклического кода.

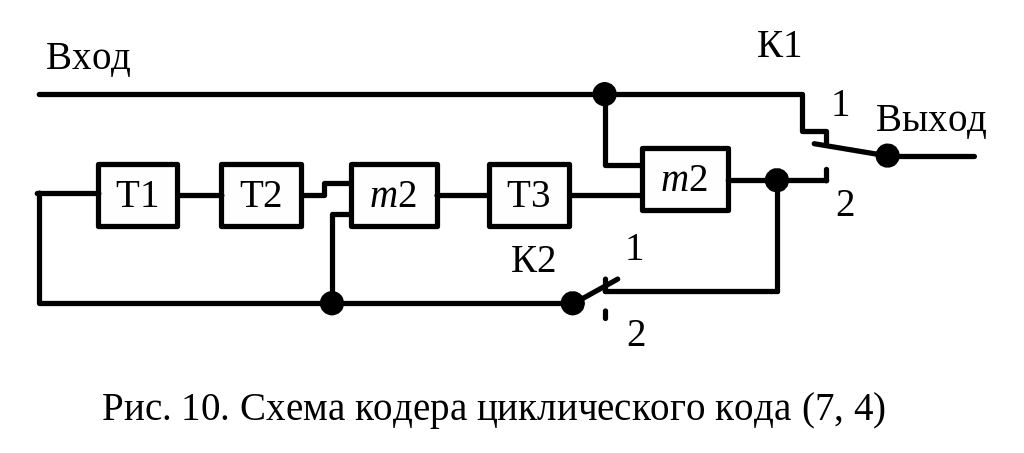
Рис. 10. Схема кодера циклического кода (7, 4)

Кодер циклического кода (7, 4) с порождающим полиномом f (х) = х³ + х² + 1 (рис. 10) состоит из трех ячеек сдвигающего регистра со связями, двух сумматоров по модулю 2 и двух ключей.

В исходном состоянии ключи К1 и К2 находятся в состоянии 1. Информационные символы поступают одновременно на выход канала и выход ячейки 3 (х³) сдвигающего регистра, так что производится умножение А(х)х³. В течение четырех тактов производится выдача информационных символов на выход кодера а также деление многочлена А(х)х³ на образующий многочлен х³ + х² + 1 (делитель образован связями в сдвигающем регистре). В результате в регистр записываются проверочные символы (остаток от деления многочлена А(х)х³ на образующий многочлен). Начиная с пятого такта, ключи К1 и К2 перебрасываются в состояние 2 и в течение трех последующих тактов проверочные символы передаются в канал связи.

Циклический код может быть задан проверочным многочленом Н(х): кодовая комбинация В(х) принадлежит данному циклическому коду, если

,

т. е. делится нацело на полином х^п + 1.

Проверочный полином связан с порождающим полиномом соотношением

.

Задание кода проверочным многочленом эквивалентно заданию кода системой уравнений. Характерной особенностью циклического кода является то, что все проверочные уравнения можно получить из одного путем циклического сдвига индексов символов, входящих в исходное уравнение. Например для кода (7, 4) с порождающим полиномом G(х) = х³ + х² + 1 проверочный многочлен имеет вид

.

Проверочные уравнения получаются из условия

.

Осуществив умножение и приравняв коэффициенты при х⁴, х⁵, х⁶ к нулю, получаем следующие уравнения относительно проверочных символов:

На основе этих проверочных уравнений строится кодер (и декодер).