1. Формирование (n, k) кода с обобщенной проверкой на четность

Рассмотрим вопрос формирования (задания) (n, k) кода с проверкой на четность.

Такой код содержит N_р = 2 ^k разрешенных кодовых комбинаций, а остальные N - N_р = 2 ⁿ - 2^k не используются и относятся к группе запрещенных.

Описание такого кода можно осуществить с помощью порождающей (образующей) матрицы, каждая строка которой имеет длину n (кодовое слово, содержащее n символов), а количество строк k определяет количество разрешенных кодовых комбинаций:

.

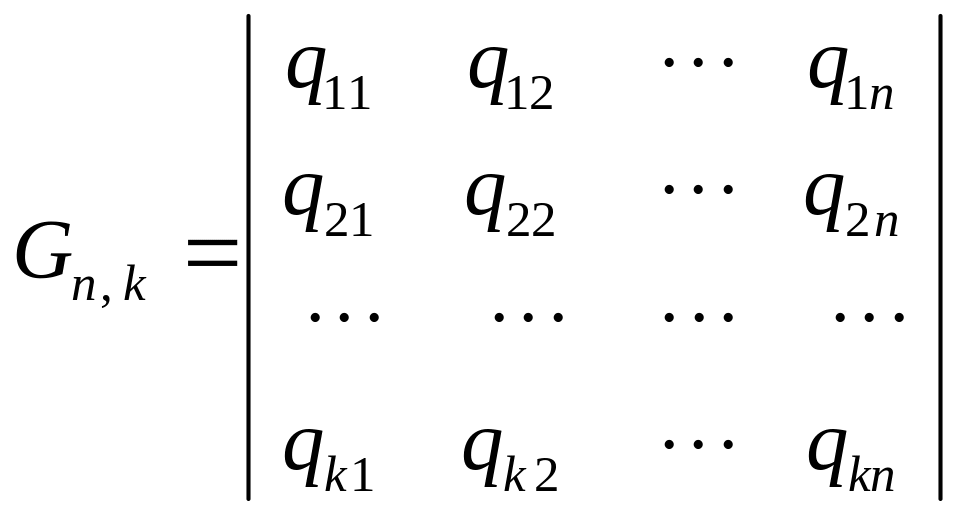Порождающая матрица G_{n, k} может быть представлена совокупностью двух матриц:

- информационной G_{k , k} , размерностью k × k , отражающей информационные кодовые символы всех разрешенных кодовых слов;

- проверочной B_{r, k} размерностью r × k, отражающей всю совокупность проверочных символов разрешенных кодовых слов:

На практике в качестве информационной матрицы используется единичная матрица Е_k:

.

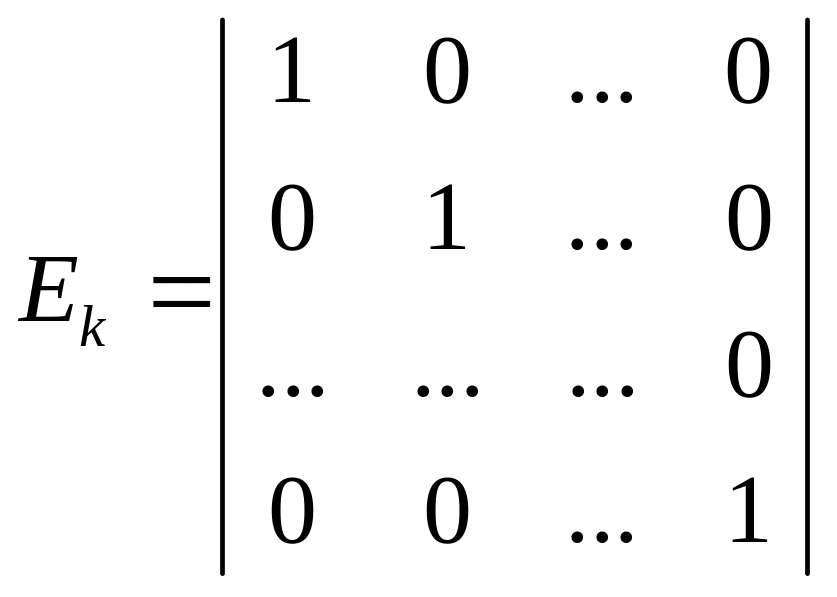Проверочная матрица B_{r, k} строится путем подбора различных r–разрядных комбинаций, удовлетворяющих условиям: количество единиц в строке должно быть не менее d_min – 1 (ω_стр ≥ d_min – 1); сумма по модулю 2 любых двух строк должна быть не менее d_min – 1 единиц.

Все возможные разрешенные кодовые комбинации строятся на основе линейного комбинирования строк порождающей матрицы.

Для построения и декодирования более удобной является так называемая проверочная матрица Н, состоящая из r строк и n столбцов. Образуется проверочная матрица следующим образом.

Вначале строится единичная матрица Е_k , затем к ней слева приписывается матрица B_{k, r} , состоящая из k столбцов и r строк, причем каждая ее строка соответствует столбцу проверочных разрядов матрицы B_{r, k} порождающей матрицы G_{n, k} , т. е. B_{k, r} = В_{r, k} ^Т:

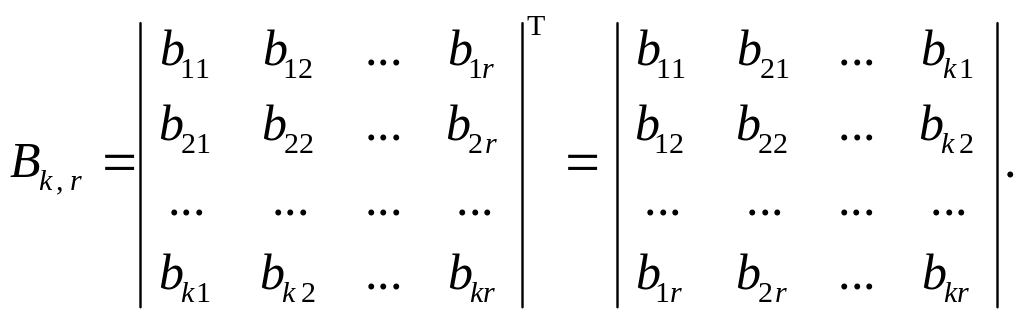
Проверочная матрица при этом имеет вид

.

С помощью проверочной матрицы очень просто определяются значения неизвестных проверочных символов по известным информационным символам. Для этого составляется система уравнений проверок на четность (так называемых проверочных уравнений), каждое из которых представляет собой сумму тех информационных разрядов, которые в i-й строке матрицы B_{k , r} помечены единицами.

Пример. Построить порождающую и проверочную матрицы систематического кода, предназначенного для передачи 16 сообщений и способного исправлять одиночные ошибки.

Для такого кода число разрешенных кодовых комбинаций N_р равно 16, откуда определяем число информационных символов k = 4. Для исправления одной обнаруженной ошибки код должен иметь кодовое расстояние d_min = 3.

Определим общее число символов в кодовой комбинации из условия соотношения общего числа символов и числа информационных символов:

, , из чего следует .

Из представленного выражения находим: n = 7, r = 3, k = 4.

Таким образом, порождающая матрица состоит из единичной матрицы размером 4 × 4 и проверочной матрицы размером 3 × 4. С учетом того, что количество единиц в строке должно быть не менее d_min – 1, т.е. не меньше 2, а общее число проверочных кодовых символов равно 3, в качестве проверочных выберем следующие комбинации: 111, 110, 101 011.

В проверочную матрицу B_{r, k} = B_3,4 эти комбинации могут входить в произвольном порядке, так что можно получить несколько равнозначных проверочных матриц:

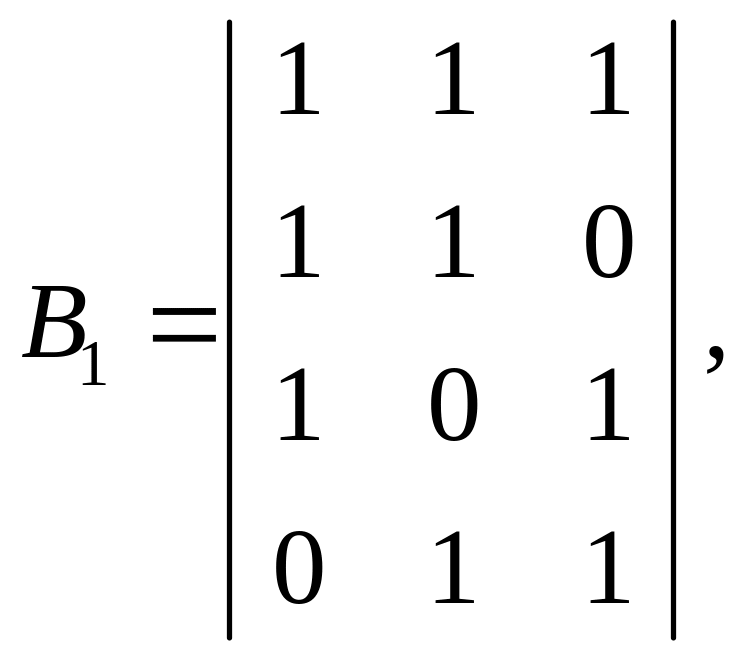
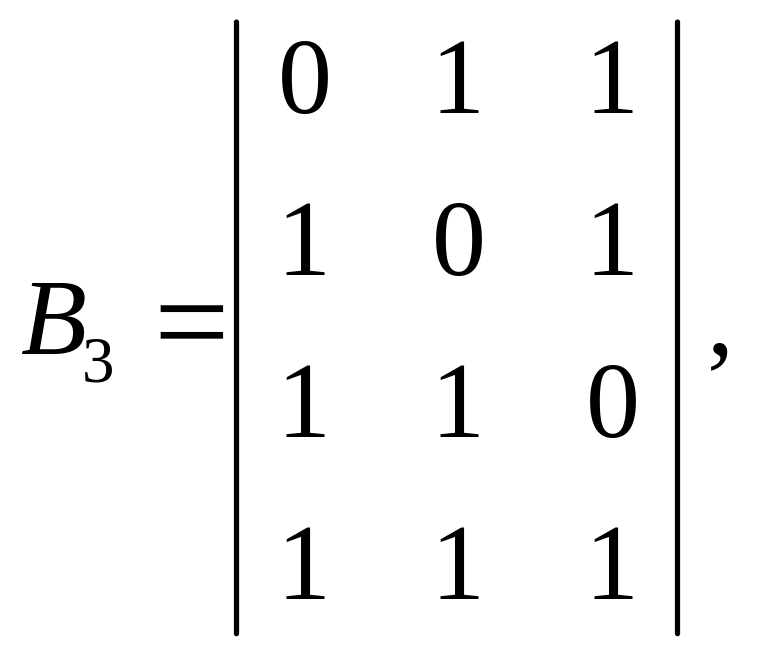
причем с любой из них может быть построена порождающая матрица. Так, например, для В₂ имеем

.

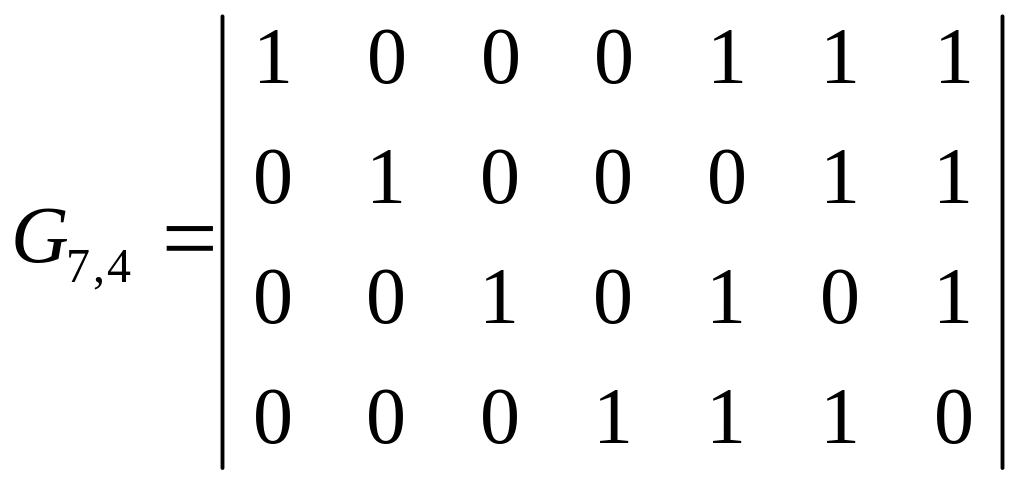С учетом нулевой комбинации 0000000 и четырех комбинаций порождающей матрицы могут быть получены все 16 разрешенных кодовых комбинаций, для чего следует произвести все возможные суммирования строк порождающей матрицы.

Для построения проверочной матрицы Н по известной порождающей матрице G_{7, 4} найдем сначала матрицу В_{4, 3} , которая является транспонированной к матрице В_{3, 4} из состава порождающей матрицы G_{7, 4}:

, откуда

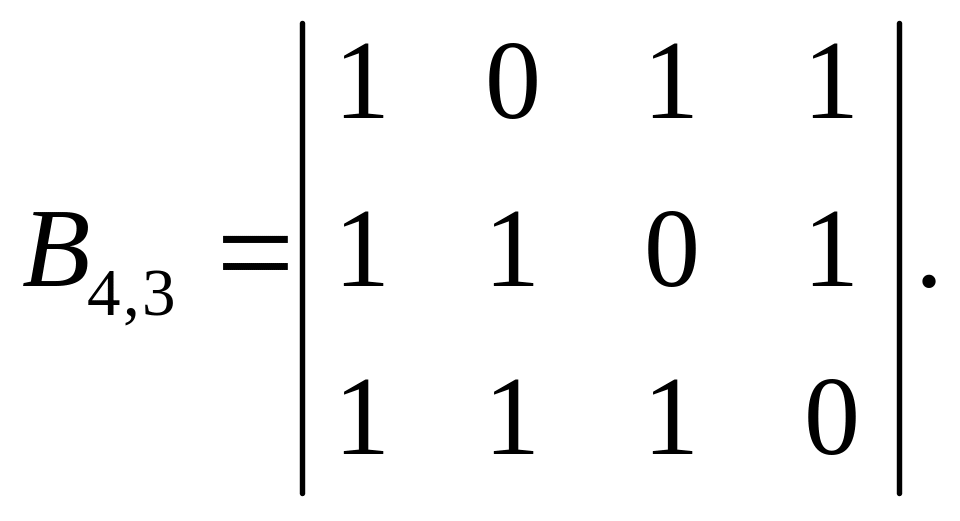
После приписывания к ней единичной матрицы Е₃ имеем проверочную матрицу

.

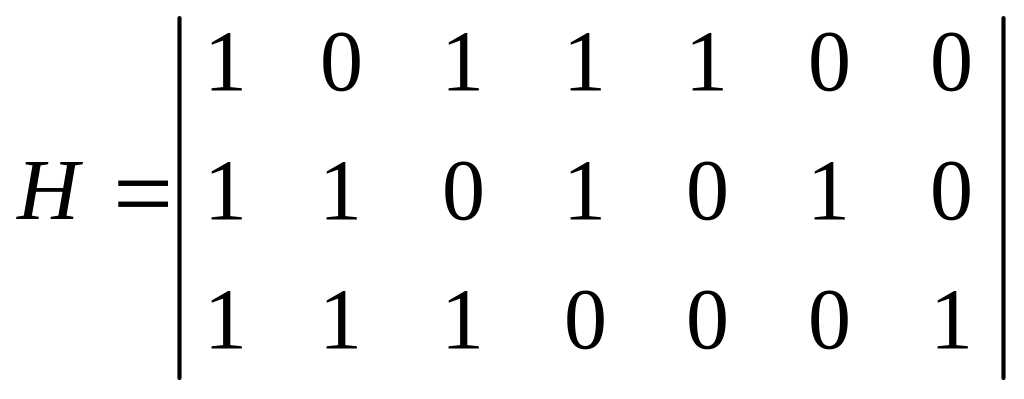По этой матрице составляем систему проверочных уравнений для определения системы проверочных символов:

b₁ = a₁ + a₃ + a₄;

b₂ = a₁ + a₂ + a₄;

b₃ = a₁ + a₂ + a_3.

С помощью этой системы легко закодировать любое сообщение. Пусть, например, необходимо передать информационную комбинацию 0 1 0 0. Тогда

b₁ = 0 + 0 + 0 = 0;

b₂ = 0 + 1 + 0 = 1;

b₃ = 0 + 1 +0 = 1,

и кодированное сообщение имеет вид 0 1 0 0 0 1 1.

Допустим, что передавалось сообщение 0 1 0 0 0 1 1, но под действием мешающих факторов была принята кодовая комбинация 0 1 0 1 0 1 1, т. е. ошибка наблюдается в четвертом разряде. Проверочные уравнения, закладываемые в алгоритм декодера, дают результат:

b₁ = a₁ + a₃ + a₄ = 0 + 0 + 1 = 1;

b₂ = a₁ + a₂ + a₄ = 0 + 1 + 1 = 0;

b₃ = a₁ + a₂ + a_3.= 0 + 1 + 0 = 1.

Замечаем, что результаты двух первых проверочных уравнений показывают наличие ошибки, а третье уравнение – отсутствие ошибки. Из него следует, что символы a₁ , a₂ , a₃ переданы без ошибки, а символ a₄ – с ошибкой.

Таким образом:

- порождающая матрица G_{n, k} позволяет представить весь набор кодовых комбинаций в удобной и компактной форме. С помощью этой матрицы можно достаточно просто построить кодовую комбинацию по известным информационным символам, т. е. представить неизбыточное сообщение в закодированном данным кодом виде;

- проверочная матрица Н_{n, r} обычно используется для построения кодирующих и декодирующих устройств, так как определяет алгоритм нахождения проверочных разрядов по информационным символам;

- проверочная матрица очень удобна для нахождения места ошибки в принятой кодовой комбинации.

В настоящее время существует большое количество разнообразных линейных кодов, которые строятся на основе обобщенных проверок на четность. К ним относятся коды Хэмминга, Голея, Рида – Маллера и др.