1. Общие принципы построения помехоустойчивых кодов

Одним из важнейших требований, предъявляемых к системам передачи информации (СПИ) по радиоэфиру, является обеспечение высокой достоверности принимаемых сообщений. Вероятность ложных сообщений в таких системах не должна превышать значений Р = 10^-6 ... 10^-9, тогда как вероятность ошибочного приема единичного элемента в современных системах связи редко меньше 10^-3 ... 10^-4. Поэтому для повышения достоверности сообщений применяют специальные меры, снижающие вероятность появления ошибок до некоторого допустимого уровня. Одним из наиболее эффективных средств обеспечения высокой достоверности принимаемых сообщений является использование избыточных кодов.

Помехоустойчивые коды это коды, обеспечивающие высокую достоверность передачи сообщений. В основе их построения лежит избыточность, когда для передачи информации используется только часть кодовых комбинаций, называемая разрешенной. Кодовые комбинации, относящиеся к разрешенным, отличаются друг от друга более чем в одном разряде. Другая (запрещенная) часть кодовых комбинаций не используется. Ее прием свидетельствует о наличии ошибки в сообщении.

Пусть п – число символов в кодовой комбинации, из которых k символов используются для передачи информации, а п – k символов не несут информации. Иначе говоря, из общего числа N = 2^п кодовых комбинаций используется N_р = 2^k разрешенных, а остальные кодовые комбинации N - N_р = 2^п – 2^k относятся к группе запрещенных.

При использовании избыточных кодов ошибка в одном разряде разрешенной кодовой комбинации приводит к ее замене на запрещенную.

При достаточно большом отличии разрешенных кодовых комбинаций друг от друга прием запрещенной кодовой комбинации позволяет обнаружить однократную, двукратную и т.д. ошибки. Вместе с тем переход одной разрешенной кодовой комбинации в другую не позволяет обнаружить ошибки (рис. 5).

Поясним способность кода исправлять ошибки. Разобьем множество всех запрещенных комбинаций (N - N_р) на N_р подмножеств. Каждому i-му подмножеству поставим в соответствие одну разрешенную В_i кодовую комбинацию. Зададимся правилом приема: если принятая кодовая комбинация попадает в j–е подмножество, то принимается решение о приеме В_j кодовой комбинации. Очевидно, что при таком подходе будут исправляться все ошибки, не выводящие передаваемую кодовую комбинацию за пределы принадлежащего ей подмножества.

Разрешенные

кодовые

комбинации

Запрещенные

кодовые

комбинации

Канал

связи

Помехи

Источник

Приемник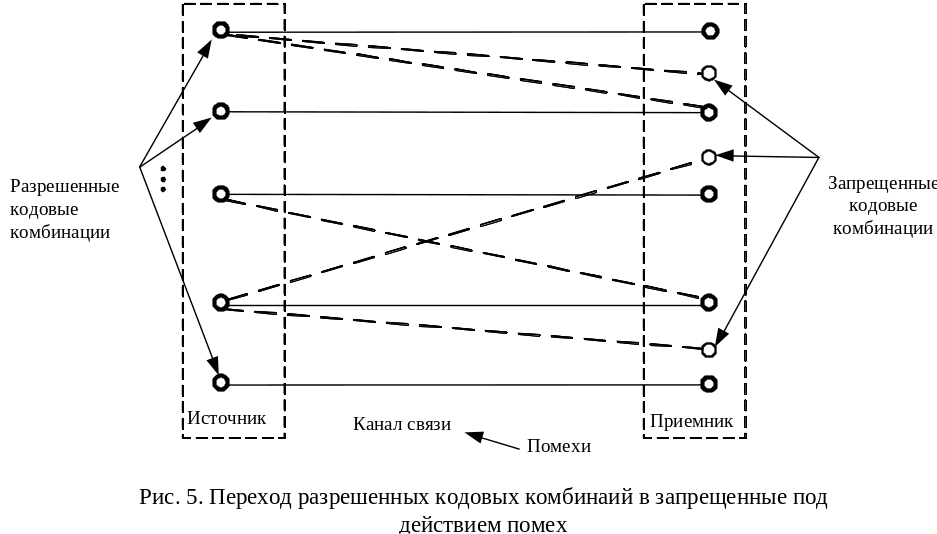

Рис. 5. Переход разрешенных кодовых комбинаий

в запрещенные под действием помех

При построении кода, работающего в режиме декодирования с исправлением ошибок, основной сложностью является разбиение множества запрещенных комбинаций на подмножества и сопоставление каждому из них разрешенной кодовой комбинации.

В общем случае, когда разрешенные кодовые комбинации выбираются произвольным образом (так называемое случайное кодирование), код можно задать таблицей соответствия между сообщениями и разрешенными кодовыми комбинациями. В этом случае кодер будет представлять собой запоминающее устройство, в памяти которого хранится набор разрешенных кодовых комбинаций. Соответственно, может быть реализован универсальный метод декодирования: каждая принятая кодовая комбинация последовательно сравнивается с каждой разрешенной кодовой комбинацией. Решение принимается в пользу той разрешенной кодовой комбинации, которая отличается от принятой комбинации в меньшее число символов. Очевидно, что и декодер должен хранить в своей памяти все разрешенные комбинации. Несмотря на универсальность, методы не нашли применения на практике из-за большого объема памяти при кодах большой длины и существенных временных затрат, связанных с декодированием.