Построение кодового дерева Шеннона-Фано

Знаки исходного алфавита и частоты их появления	Разделение списка на группы 1-го уровня	Разделение списка на группы 2-го уровня	Разделение списка на группы 3-го уровня	Знак и его представление в двоичном виде
А  9	17  0	9  0		А  00
Д  8		8  1		Д  01
Б  7	13  1	7  0		Б  10
В  5		6  1	5  0	В  110
Г  1			1  1	Г  111

Замечаем, что никакая кодовая комбинация не является префиксом никакой другой кодовой комбинации этого кода.

Чтобы декодировать префиксный код, необходимо декодировать последовательно всю кодовую комбинацию. Поскольку конец кодовой комбинации всегда может быть опознан (далее в цифровом потоке идет префикс, а он опознается однозначно - свойство префикса), то декодирование выполняется без задержки принимаемой последовательности. По этой причине префиксные коды еще называются мгновенными.

Если все кодовые комбинации префиксного кода, за исключением, может быть, последней, заканчиваются нулем, то код называется кодом с запятой.

Пример: а1 = 0; а2 =10; а3 = 110; а4 = 111.

Альтернативный алгоритм эффективного кодирования, минимизирующий длину кодированного сообщения, был предложен Д.А. Хаффменом.

Классический алгоритм Хаффмена на входе получает таблицу частот встречаемости элементов в сообщении (рис. 4) или таблицу вероятностей появления символов, на основании которых строится дерево кодирования Хаффмена (Х-дерево).

Правило построения и пример кодового дерева Хаффмена представлены на рис. 4.

Частота

появления

символов

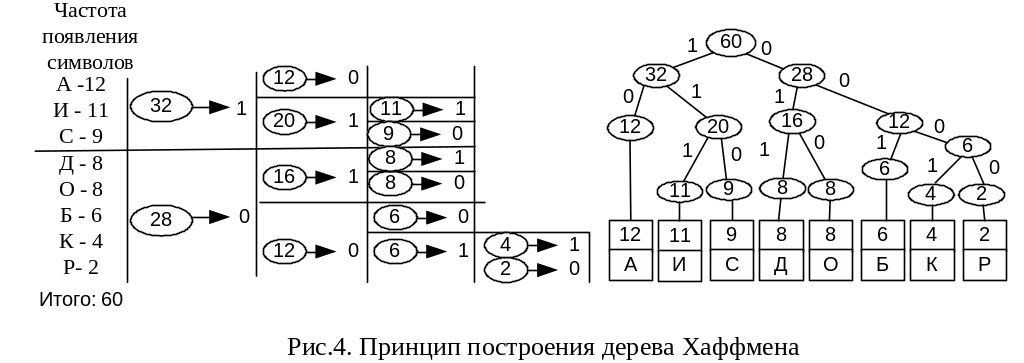
Рис. 4. Принцип построения дерева Хаффмена

Заметим, что, используя кодовое дерево, можно составить любую кодовую комбинацию путем обхода дерева от корня к листу, например: С – 110; К - 0001.

Задачи

1. Источник может выдавать 10 сообщений, вероятности появления которых равны: С = 0,05; А = 0,3; О = 0,2; М = 0,04; Л = 0,03; Е = 0,1; Т = 0,02; Ч = 0,01; И = 0,1; К = 0,15. Для передачи сообщений построить код Шеннона – Фано.

2. Для условия задачи 1 построить дерево кодов Хаффмена.

3. Закодировать кодом Хаффмена сообщение: «МОЛОТ».

4. Закодировать кодом SSS (3, 2, 12) сообщение, номер которого равен 83.

5. Закодировать НДК сообщение, номер которого равен 83.

6. Перевести код символа 011001 из НДК в код Грэя.

7. Перевести код символа 011001 из кода Грэя в НДК.

Контрольные вопросы

1. Перечислите достоинства кода Грэя, определяющие область применения.

2. Какой код называется префиксным?

3. Поясните условие, при выполнении которого возможна передача сообщений, вырабатываемых дискретным источником, по каналу связи.

4. Поясните сущность экономного кодирования.

5. Какие коды называются мгновенными?

6. В чем разница декодирования кодов Шеннона – Фано и МТК–5?

4. ПОМЕХОУСТОЙЧИВЫЕ БЛОЧНЫЕ КОДЫ