2. Анализ исследуемой системы

2.1. Исследование устойчивости системы

2.1.1 Частотный критерий устойчивости.

При исследовании устойчивости системы частотным методом используется частотный критерий устойчивости Найквиста применительно к логарифмическим частотным характеристикам системы. Для этой цели строятся асимптотические логарифмические характеристики разомкнутой системы. Исходным для построений логарифмических характеристик является выражение (24) передаточной функции разомкнутой системы [2].

Для построения асимптотической логарифмической амплитудной характеристики разомкнутой системы, определяем частоты сопряжения и ординату единичной частоты :

Частота сопряжения [1]:

(25)

_{Подставив полученные значение Тоб в выражение (25) получим частоту сопряжения заданной системы:}

ω = = = 20

Ордината единичной частоты [1]:

L₁(1) = 20·lg К (26)

L₁(1) = 20·lg 3,58 = 11(дБ)

Построим логарифмическую фазовую характеристику для передаточной функции системы, используя выражение для вычисления фазового угла [1]:

φ(ω) = -90-arctg (T_об· ω) (27)

Подставим значения Тоб в выражение (24) получим: φ (ω) = - 90 -arctg (0,05· ω) (28)

Для построения логарифмической фазовой характеристики ЛФХ производим расчет точек зависимости φ(ω). Расчеты представлены в таблице 2.

Таблица 2. Точки для построения ЛФХ

№	ω, рад/с	φ(ω), град
1	0	-90
2	1	-93
3	10	-126,5
4	20	-135
5	40	-153,5
6	100	-168,7
7	∞	-180

График логарифмической амплитудно-частотной характеристики состоит из двух интервалов:

Интервал низких частот (₁) в виде прямой линии с наклоном -20 дБ/дек, по отношению к оси частот будет проходить через точку ( =1; L₁(1)), согласно свойствам интегрирующего звена.

Интервал высоких частот (₁<). При частоте, равной первой частоте сопряжения ₁ начинает влиять инерционность датчика на систему, поэтому наклон прямой по отношению к оси частот увеличится на -20 дБ/дек [1].

Построенные ЛАХ и ЛФХ системы без учета влияния регулятора изображены на чертеже КР-2068.998-26-06-00.00.000.Д1 кривыми L₁(ω) и φ₁(ω). По построенным графикам видно, что система является устойчивой по частотному критерию, так как _ср<_π.

2.1.2 Оценка устойчивости системы при помощи алгебраического критерия Гурвица

Критерий Гурвица использует для оценки выполнения условия устойчивости системы коэффициенты характеристического полинома замкнутой системы, выражение (24).

Первым условием устойчивости САУ по Гурвицу является положительность всех коэффициентов характеристического уравнения замкнутой системы :

с₀ = 0,05> 0; с₁ = 1> 0; c₂ = 3,58 > 0.

Вторым условие устойчивости является положительность всех определителей, составленных из коэффициентов характеристического полинома на основе таблицы Гурвица :

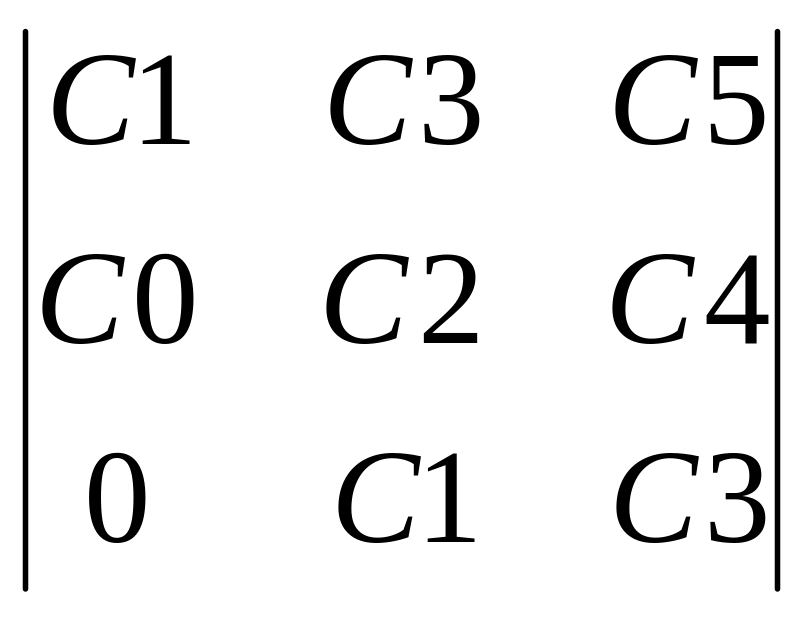
∆₂ = = с₁·с₂-(0·с₀) =1*3,58 - 0*0,05=3,58 > 0.

Критерий устойчивости Гурвица подтверждает устойчивость полученной системы, так как выполняются оба условия устойчивости.