2.12. Оптимальное упр. Позиционным электроприводом.
Позицион ЭП должен отрабатывать заданное перемещение с заданной степенью точности. Возможны 3 варианта постановки задачи оптимального управления.
1) При ограничении на потери необходимо отработать max возможное перемещение
.
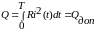2) Необходимо отработать заданное перемещение при минимальных потерях
.
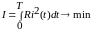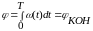
3) Необходимо отработать заданное перемещение при ограничениях на потери за минимальное время
..
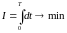
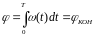
Рассмотрим 1-ый вариант
Cоставляем функцию Лагранжа
.
.
.
.
.
.
.
.
;
;
;
;
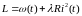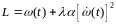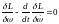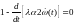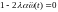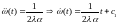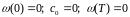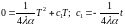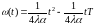О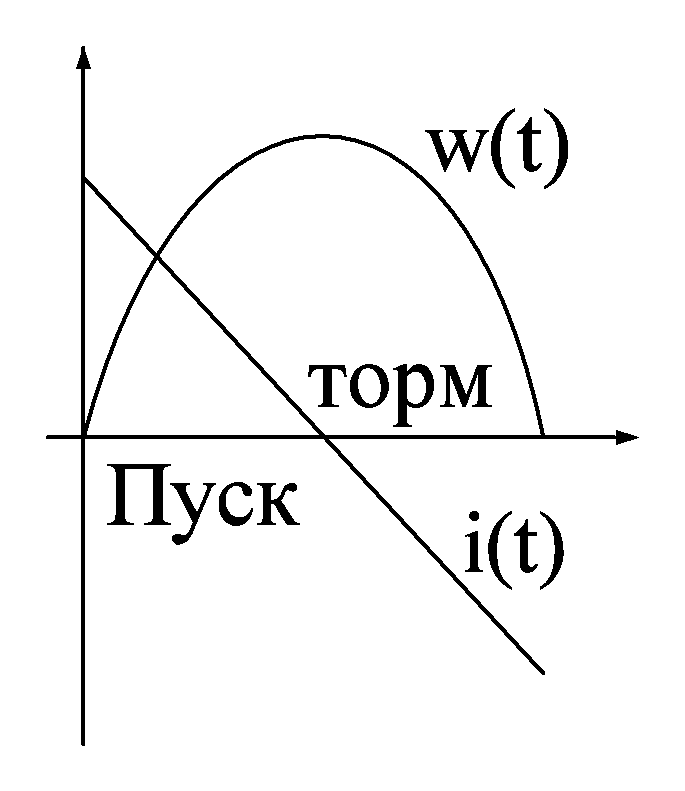
птимальным
законом изменения скорости является
параболический закон. А ток должен
изменятся по линейному закону.
Зная величину
перемещения
,
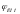а также допустимые потери можно определить
время обработки перемещения Т.
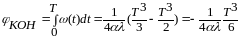(1)
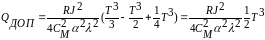(2)
Из (1) и (2) можно
найти
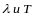
2.13. Синтез сау методом модального управления
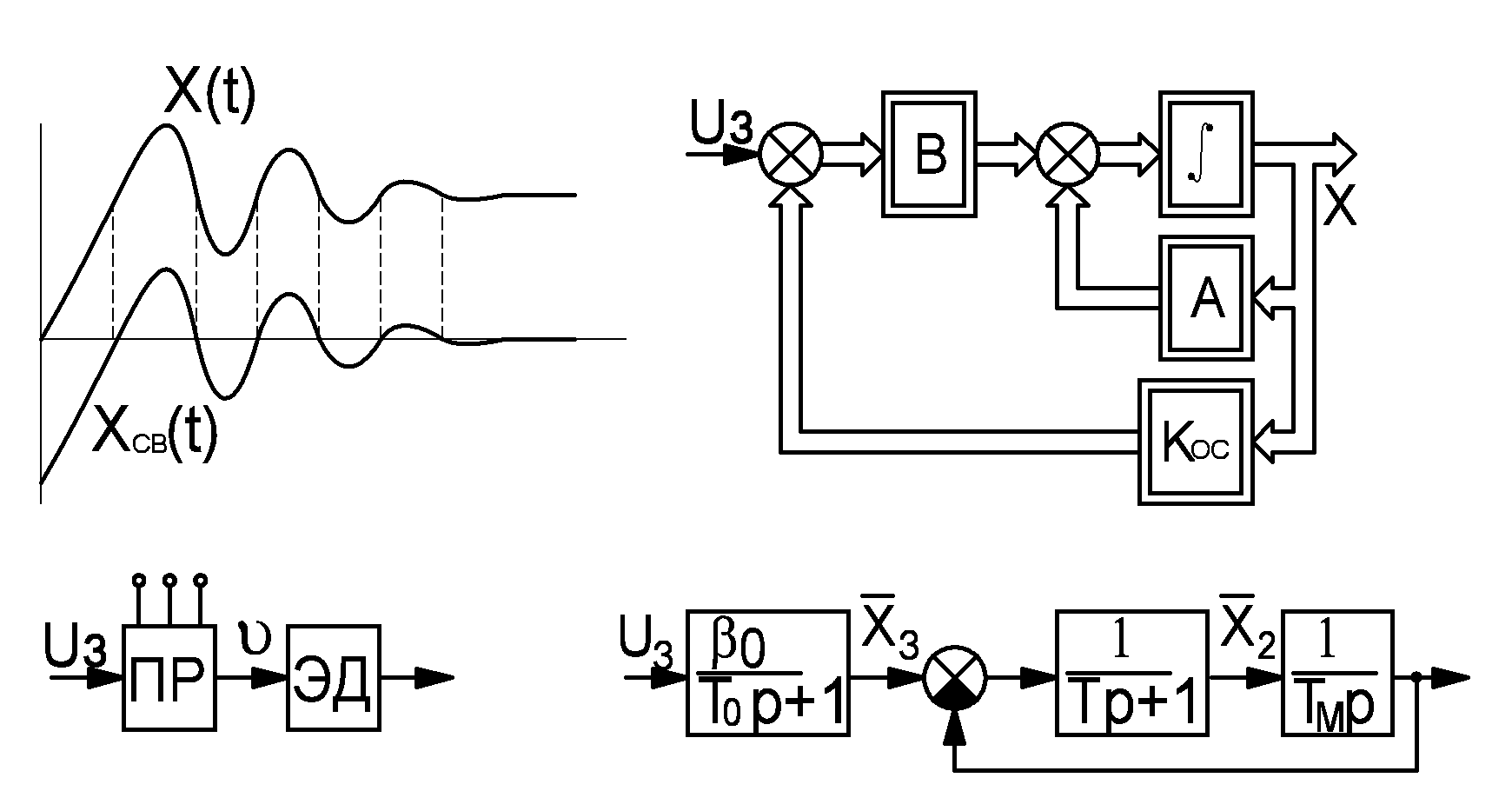
Любое движение системы можно представить суммой 2-х составляющих: вынужденное и свободное.
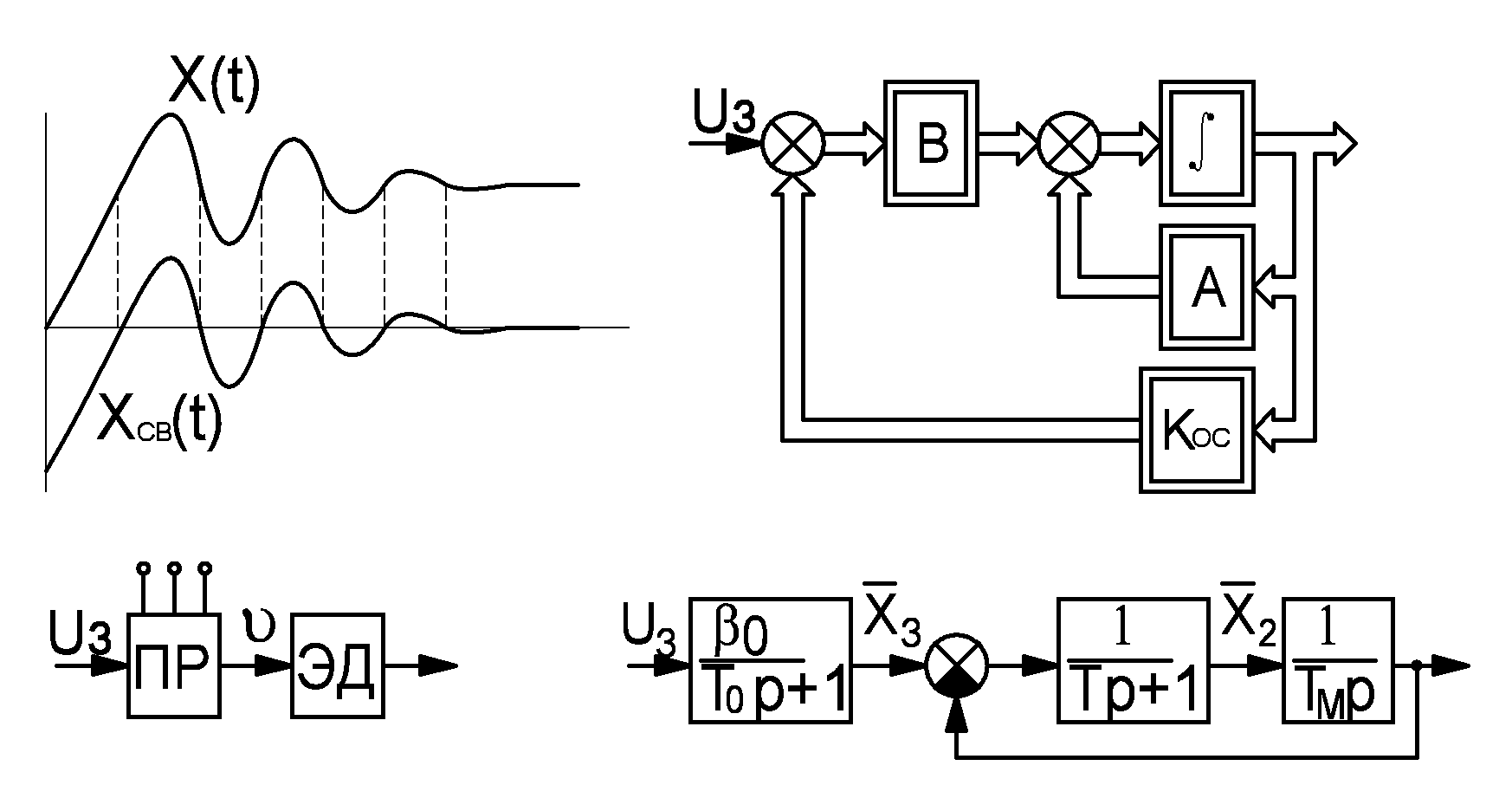
Дин. св-ва с-мы определяются свободной составляющей. Поэтому, упр. свободной составляющей можно тем самым управлять динамическими свойствами системы.
П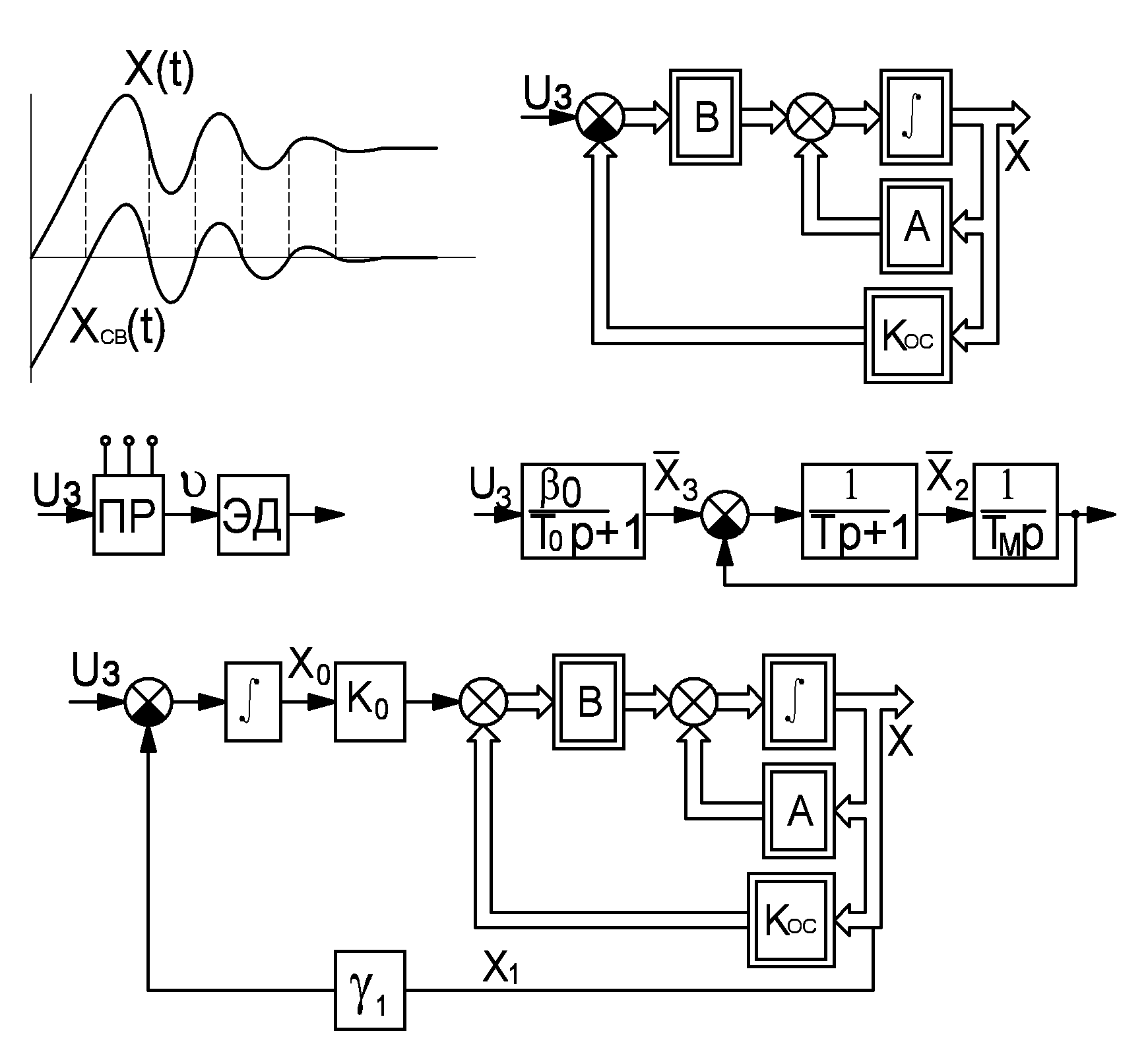
ри
использовании модального упр., упр.
является линейной функции координат
объекта.
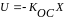
Кос – матрица коэфф. обратных связей.
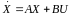
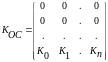
Все коэф Кос=0, кроме последнейстроки. Это делается по 2-ум причинам:
1 – за счет одной строки матрици можно получить любые собственные значения матрици => любые установившиеся свойства системы.
;
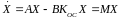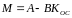
Динамические свойства системы будет определятся собственными матрицы М.
2 – в реальных системах непосредственно можно воздействовать только на старшую производную объекта.
; 
;
; 
;
; 
.
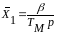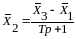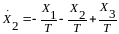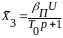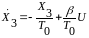Метод модального упр., используются для синтеза астатических САУ. Дело в том, что в астатических системах имеется определенная связь между дин. и . св-ми системы. Поэтому получив нужные дин. св-ва статические св-ва могут оказаться неудовлетвор.
Что же касается
астатический систем, то здесь такой
проблемы не возникает, т к получив нужные
динамические, статические свойства
получаются автоматически, т к
.
Для того, чтобы система была астатической, необходимо в канал главной ошибки ввести астатическое звено (интегратор), т е вводится дополнительная координата.
;
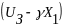- главная ошибка.
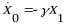
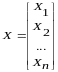- исходное векторное
состояние.
Вектор состояний
для расширенного объекта.
Тогда уравнение
состояний для расширенного объекта:
.
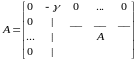- матрица
коэффициентов для расширения системы.
;
;
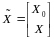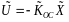В итоге структурная схема:
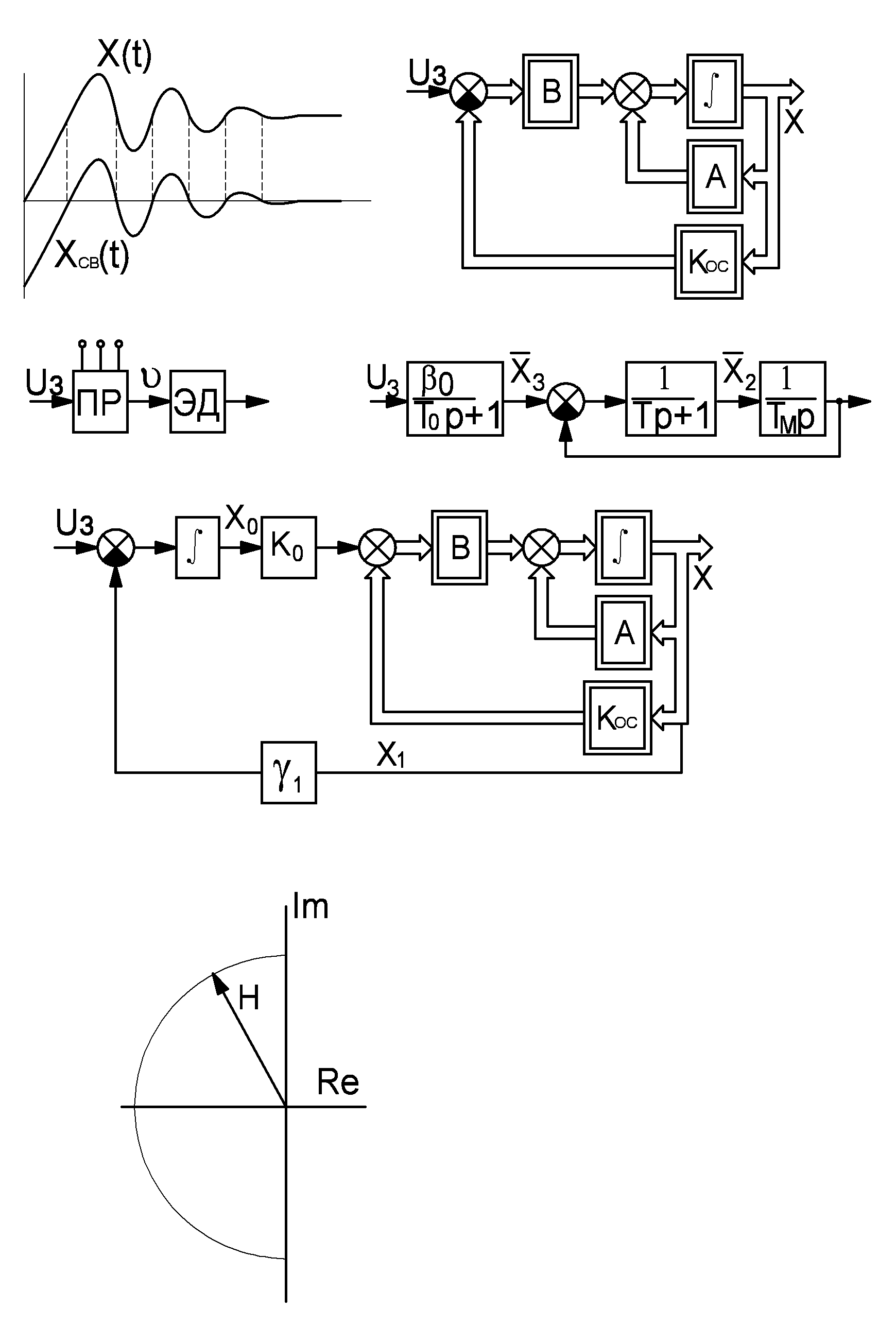
Целью синтеза системы является определение коэффициента матрицы обратных связей Кос, изходя из заданных динамических свойств системы.
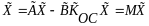где
.
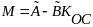Собственные значения матрицы М будет определять динамические свойства системы. Согласно Т. Виета.
(1)
Задавшись собственными значениями матрицы М (pi) и приравняв коэффициенты при одинаковых степенях p равенства (1) можно составить систему уравнений, для нахождения неизвестных коэффициентов Кос.
Один из вариантов задания собственных значений – это распределение по Батервольту. (Модуль собственных значений один)
Тогда
n – порядок расширенного объекта;
i - порядок номера собственного значения.
При распределении по Батервольту динамические свойства системы в зависимости от порядка.
При синтезе САУ возможны 2-а случая:
1 – все координаты объекта измеряемы.
В этом случае теории можно получить любое быстродействие системы (любое время регулирования)
2 – не все координаты объекта измеряемы.
В этом случае получить любое быстродействие системы не представляется возможным. Оно будет определяться параметрами объекта управления.
Метод модального управления может быть использован, когда объект представлен в виде уравнений состояний. В этом случае необходимо воспользоваться матричным методом.
Метод модального управления может быть использовать, если объект представляем в виде структурной схемы или передаточной функцией, в этом случае можно пользоватся оперативным методом (не используя матрицы).
На основании структурной схемы составляется общая структурная схема системы управления
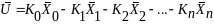
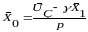
В общем случае структурная схема будет иметь вид:
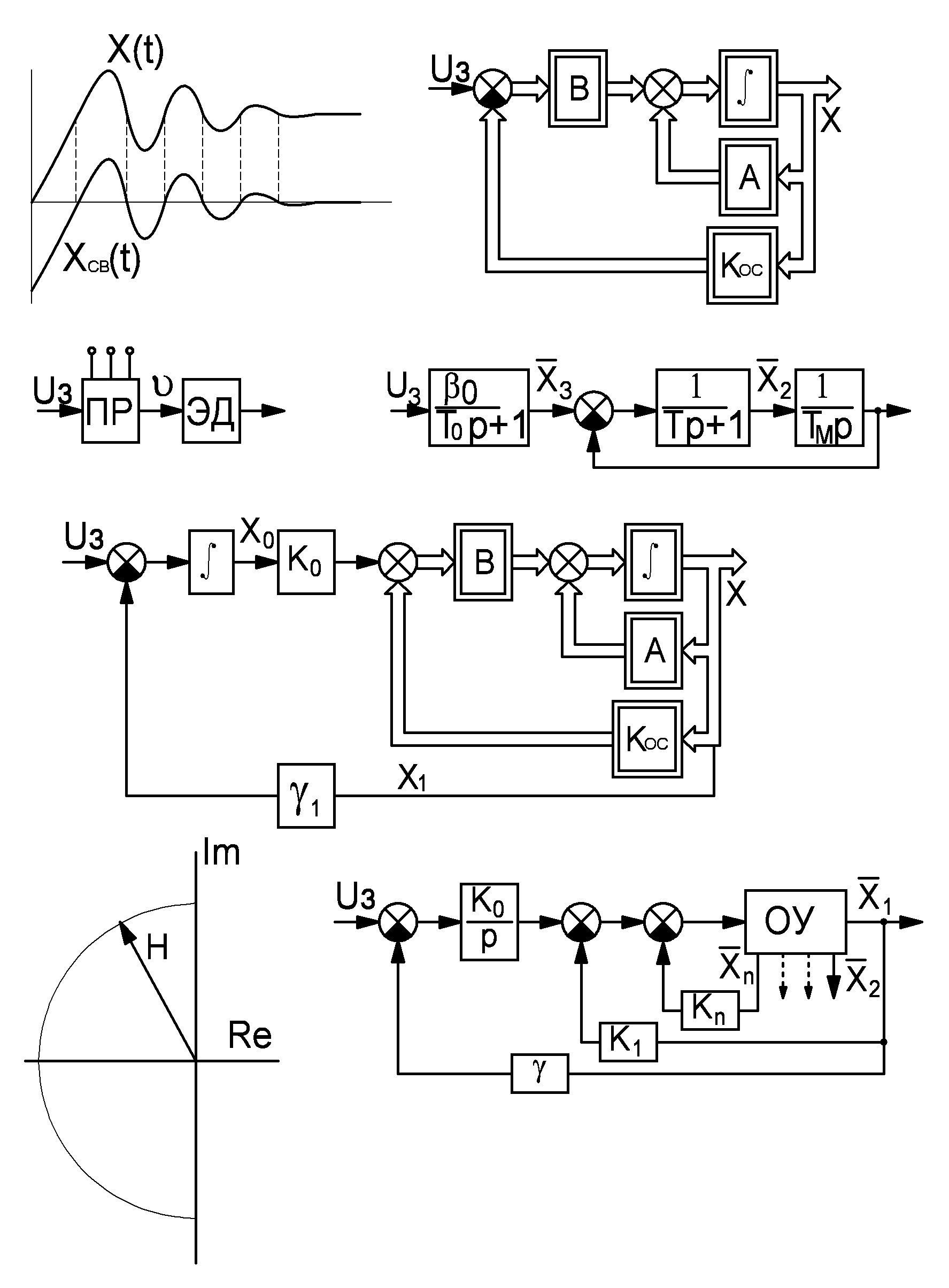
По структурной схеме записывается оптимальное уравнение и передается функция системы.
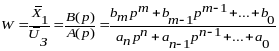
На основании теории Виета характеризующее уравнение можно записать:
(2)
Задавшись
распределением корней характерного
уравнения, например по Баревольту, и
приравняв коэффициенты при одинаковых
степенях p
равенства (2) можно составить уравнения
для нахождения неизвестной коэффициенты
обратной связи
