2.7. Электродвигатель постоянного тока как объект автоматического управления . Структурная схема, передаточная функция, уравнения состояния.
П
од
объектом автоматического управления
понимают математическую модель данного
объекта. Схема замещения ДПТ НВ имеет
вид.
.
В качестве выходной координаты возьмем противоэдс E.
,
,
.
.
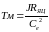Преобразуем по Лапласу
,
Н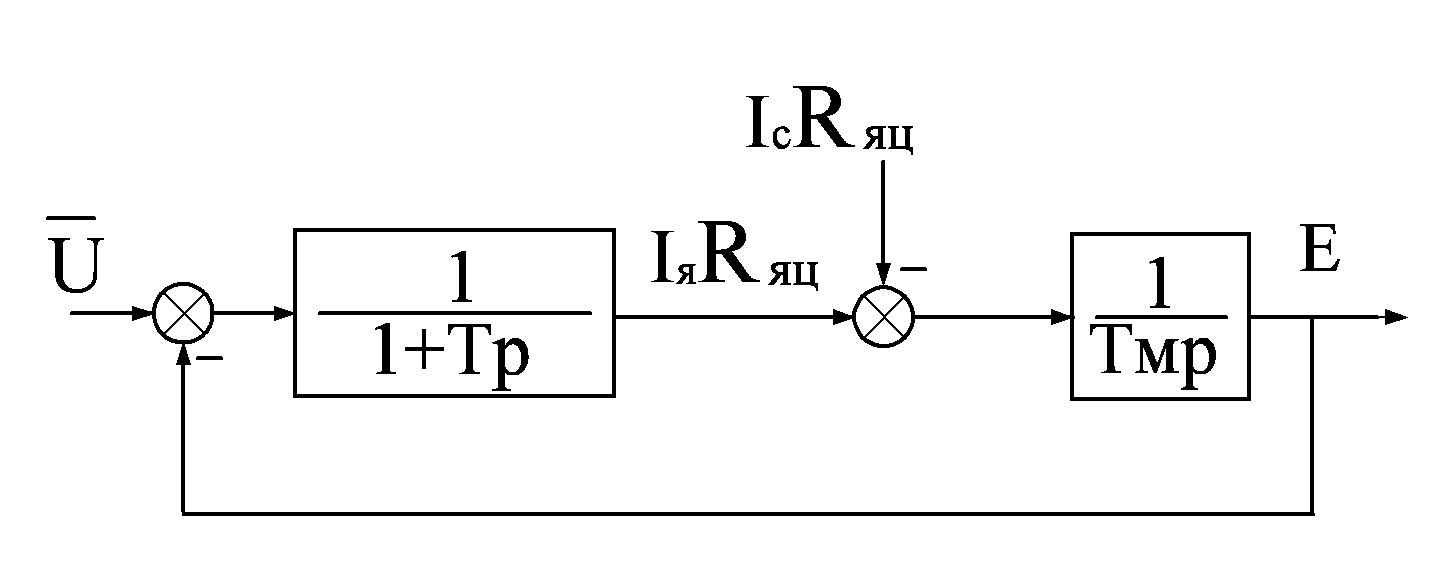
а
основании данных уравнений можно
составить структурную схему электродвигателя
постоянного тока
,
Передаточная
функция по задающему воздействию
.
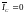Передаточная
функция по возмущающему воздействию
:
. минус означает
то, что при увеличении нагрузки скорость
будет уменьшаться.
2.8. Определение закона изменения вектора состояния объекта по уравнениям состояния.
П
о
структурной схеме переходим к уравнениям
состояния
Каждая послед. корд. должна содержать произв. от пред.
.
Закон изменения
U
известен.
.
-
известно,
.
Необходимо
определить закон изменения вектора
состояния
.
.
t0
– начальное время, t
– текущее,
-внутри (t0,t)
- фундаментальная
матрица. Согласно теореме Сильвестра
,
Е – единичная
матрица.
-
собственное значение матрицы А.
2
.9.
КРИТЕРИИ УСТОЙЧИВОСТИ ЛИНЕЙНЫХ САУ.
Под устойчивостью
понимается способность системы
самостоятельно переходить к послед.
Установившемуся состоянию после
изменения входного воздействия(возм
или задающ).
.
Свободная составляющая будет затухать,
если показатель степени будет
отрицательным. Для того чтобы система
была необходимо чтобы корни харкт.
уравн. располагались в левой комплексной
полуплоскости.
Для определения устойчивости системы существует ряд критериев, которые позволяют определить устойчивость без определения корней характеристического уравнения.
1) Алгебраический
критерий Рауса-Гурвица:
- уравнение n-ого
порядка. Система будет устойчивой если
все коэф. характеристического уравнения
положительны
,
а также положительны угловые миноры
Гурвицевой матрицы
П
ример
n=3.
,
,
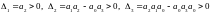
2) Частотный критерий
устойчивости Найквиста. Для того чтобы
замкнутая система была устойчивая,
необходимо чтобы была устойчива
разомкнутая система и ее АФЧК при
изменении
она не охватывала точку
.
h
– устойчивость по амплитуде;
- устойчивость по фазе.
3) Частотный критерий устойчивости Михайлова.
С
истема
будет устойчивой если годограф Михайлова
построенный по характерист. ур-ию
замкнутой системы при изменении
начинается на вещественной полуоси и
последовательно пересекает n
квадрантов нигде при этом не обращаясь
в 0.
2.10. Синтез сау методом лах.
Целью синтеза является определение структуры и параметров УУ обеспечивающей заданные статические и динамические показатели системы.
Частотные методы основаны на том что существует определенная связь между частотными и переходными характеристиками системы. Эта связь имеет вид
.
-
вещественная частотная характеристика
система(ВЧХ). Обеспечивая необходимую
ВЧХ можно обеспечить необходимые
свойства системы.
Для того чтобы перерегулирование не превышало 18% необходимо чтобы ВЧХ было положит. невозраст. -
Д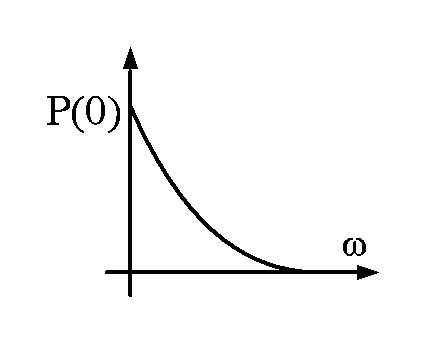
ля
того чтобы перерегулирование отсутствовало
необходимо чтобы ВЧХ была положит и
монотонно убывающей
Существует такое
понятие как частота положительности(частота
при которой
меньше 3% от P(0)).
Быстродействие тем больше чем больше
Синтез регулятора методом ЛАХ
W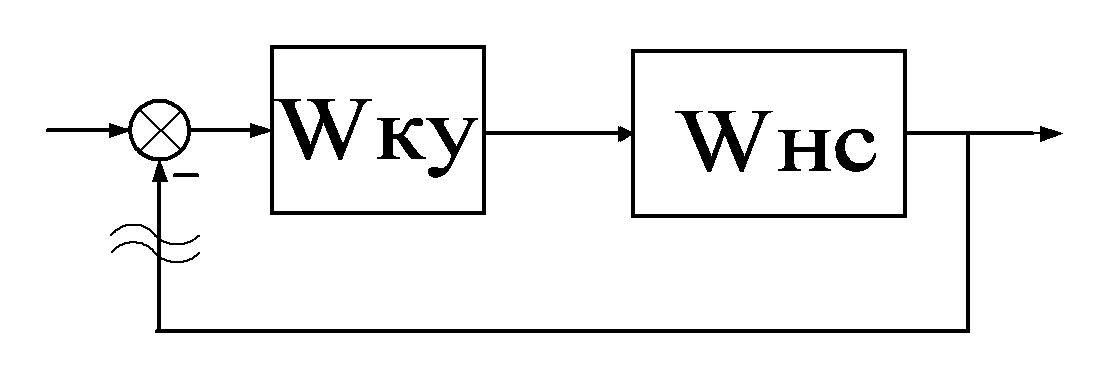
нс
– передаточная функция разомкнутой
нескорректир системы
Wку - передаточная функция корректирующего устройства которое необходимо определить
Передаточная функция разомкнутой скорретированной системы
.
.
-
желаемая ЛАХ которая обеспечивает
заданные дин. Хар-ки системы.
