
- •Кинематика сплошной среды
- •Элементы теории деформаций
- •Динамические величины и элементы теории напряжений
- •Раздел 2. (4) Уравнения механики сплошных сред
- •§ 1. Уравнение неразрывности
- •§ 2. Уравнения движения и равновесия
- •§ 3. Уравнения состояния (математические модели)
- •§ 1. Уравнение неразрывности
- •§ 2. Уравнения движения и равновесия
- •Уравнением моментов
- •§ 3. Уравнения состояния (математические модели)
- •§ 4. Уравнения состояния гидромеханики
- •§ 5. Основные уравнения теории фильтрации
- •§ 5.1 Линейные уравнения и граничные задачи фильтрации.
- •§ 6. Мгновенные уравнения состояния и критерии прочности
- •§ 7. Временные уравнения состояния и критерии длительной прочности
- •§ 8. Общая система уравнений механики деформируемого твердого тела
- •Задачи гидромеханики в бурении
- •§ 1. Базовые задачи гидродинамики при промывке и цементировании скважин
- •§ 2. Ламинарное и турбулентное течение жидкостей в щелевом канале
- •§ 3. Ламинарное и турбулентное течение жидкостей в кольцевом канале
- •§ 4. Задачи фильтрации при строительстве скважин
- •Формула дюпюи и ее обобщения
- •§1. Среды в механике сплошной среды
- •§2. Горные породы
- •§ 3. Критерии разрушения сред на основе теории трещин
- •§ 4. Порода - деформируемое твердое тело
- •§ 5. Реологические свойства
- •§ 6. Задачи устойчивости горных пород в скважинах
- •Напряженное состояние и устойчивость анизотропных пород в вертикальных и наклонных скважинах
- •4.10. Определение горного давления на крепь ствола скважины
- •4.11. Центрирование бурильных и обсадных колонн.
Напряженное состояние и устойчивость анизотропных пород в вертикальных и наклонных скважинах
1.
Рассмотрим
прежде всего случай, когда вертикальная
скважина
пройдена в упругом трансверсально-изотропном
горном массиве,
плоскость изотропии которого составляет
угол
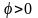 с дневной
поверхностью (рис. 64). Все остальные
предпосылки разд. 4.2 сохраняем без
изменения.
с дневной
поверхностью (рис. 64). Все остальные
предпосылки разд. 4.2 сохраняем без
изменения.
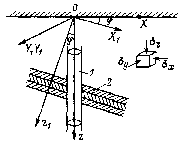
Рис. 64. Схема взаимного расположения оси скважины и плоскости изотропии
1 – скважина, 2 – пласт
Выберем
вспомогательную
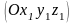 и
основную
и
основную
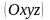 системы координат, как показано на рис.
64. В системе координат
системы координат, как показано на рис.
64. В системе координат
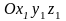 обобщенный закон Гука для
трансверсально-изотропного тела
записывается в форме (4.16). В системе
координат
обобщенный закон Гука для
трансверсально-изотропного тела
записывается в форме (4.16). В системе
координат
 повернутой
на угол
вокруг оси
повернутой
на угол
вокруг оси
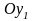 ,
согласно
формулам преобразования
[19] закон Гука (4.16) видоизменится, принимая
общий
вид, где отличными от нуля коэффициентами
преобразования
являются
,
согласно
формулам преобразования
[19] закон Гука (4.16) видоизменится, принимая
общий
вид, где отличными от нуля коэффициентами
преобразования
являются
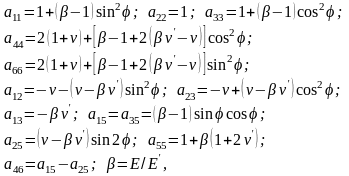
где
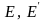 и
и
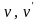 - модули упругости и коэффициенты
Пуассона, отнесенные к плоскости
изотропии и направлению, перпендикулярному
к ней.
- модули упругости и коэффициенты
Пуассона, отнесенные к плоскости
изотропии и направлению, перпендикулярному
к ней.
Так
как для нетронутого массива напряжения
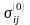 и перемещения
и перемещения
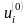 не зависят от координат х
и у,
то из уравнений равновесия (4.37), соотношений
Коши (4.40) и закона Гука имеем
не зависят от координат х
и у,
то из уравнений равновесия (4.37), соотношений
Коши (4.40) и закона Гука имеем
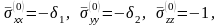
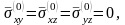 (4.70)
(4.70)
где
 и
и
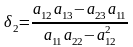 - коэффициенты бокового горного давления,
- коэффициенты бокового горного давления,
 .
.
Напряженное
состояние в приствольной зоне скважины
определим, как в разд. 4.2, суммой (в
безразмерном виде
 )
)
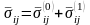 , (4.71)
, (4.71)
где
дополнительные напряжения
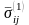 должны удовлетворять однородной системе
уравнений равновесия (4.37) и согласно
(4.70) и (4.71) — граничным условиям:
должны удовлетворять однородной системе
уравнений равновесия (4.37) и согласно
(4.70) и (4.71) — граничным условиям:
у поверхности скважины
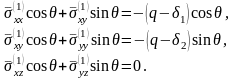 (4.72)
(4.72)
и
для удаленных от скважины точек
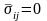 при
при
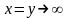 ,
где
- полярный угол в плоскости ху;
,
где
- полярный угол в плоскости ху;
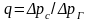 ;
;
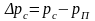 .
.
Здесь показано условие, при котором нормаль к стенке скважины направлена к оси по радиусу.
Компоненты
деформации
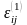 связанные с напряжениями
связанные с напряжениями
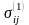 законом Гука, должны удовлетворять
условиям совместимости (4.39). Следовательно,
относительно дополнительных напряжений
имеем пространственную задачу теории
упругости для невесомого анизотропного
полупространства с цилиндрической
полостью.
законом Гука, должны удовлетворять
условиям совместимости (4.39). Следовательно,
относительно дополнительных напряжений
имеем пространственную задачу теории
упругости для невесомого анизотропного
полупространства с цилиндрической
полостью.
Уравнения
равновесия (4.37) будут удовлетворены,
если компоненты напряжений выразить
через две функции F(x,
у)
и
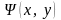 в следующем виде:
в следующем виде:
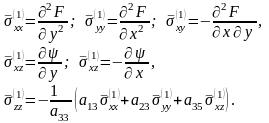 (4.73)
(4.73)
При
этом тождественно выполняются четыре
условия совместимости деформации
(4.39), а оставшиеся два сводятся к системе
дифференциальных уравнений относительно
функций F
и
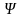 :
:
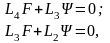 (4.74)
(4.74)
где
 - дифференциальные операторы 2-го, 3-го
и 4-го порядков;
- дифференциальные операторы 2-го, 3-го
и 4-го порядков;
Используя
зависимости (4.73) в граничных условиях
(4.72), получим, что при
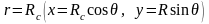 функции F
и
должны удовлетворять условиям
функции F
и
должны удовлетворять условиям
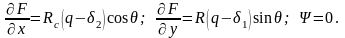
Следовательно, пространственная задача свелась к определению функций напряжения F(x, у) и в плоскости нормального сечения ху.
Подобные задачи изучены С. Г. Лехницким [19], который выразил функции F и через три аналитические функции комплексных переменных
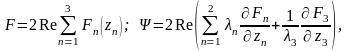
где Re – реальная часть комплексного выражения;
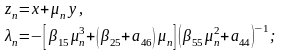
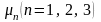 -
несопряженные комплексные (или чисто
мнимые) числа, являющиеся корнями
характеристического уравнения
-
несопряженные комплексные (или чисто
мнимые) числа, являющиеся корнями
характеристического уравнения
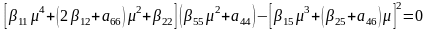 .
.
При
этом система уравнений (4.74) выполняется
тождественно и искомые функции
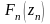 определяются только граничными условиями
определяются только граничными условиями
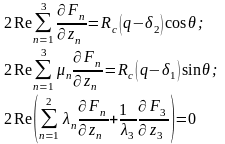
при
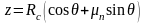 и
и
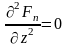 при
при
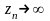 .
Эти условия будут выполнены, если выбрать
решение в виде
.
Эти условия будут выполнены, если выбрать
решение в виде
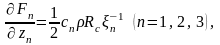
где
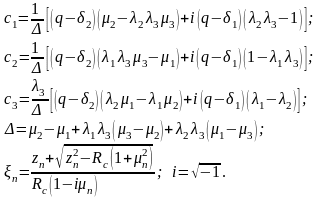
В
этом легко убедиться, если иметь ввиду,
что при
 .
.
Окончательное решение задачи удобно представить в цилиндрической системе координат, используя формулы преобразования (1.34):
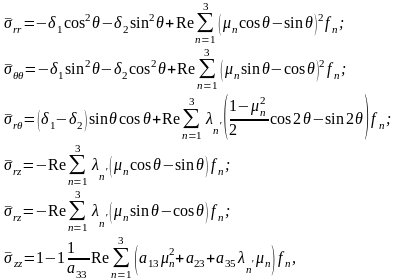 (4.75)
(4.75)
где
 для п
= 1,
2 и
для п
= 1,
2 и
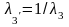 .
Распределение напряжений на стенке
скважины определяется по формулам
(4.75) при
.
Распределение напряжений на стенке
скважины определяется по формулам
(4.75) при
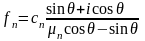 .
.
Следует
отметить, что сведения о трех механических
параметрах горного массива —
коэффициентах Пуассона v,
v'
и отношении модулей Юнга
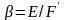 — являются достаточными для реализации
рассматриваемой задачи в напряжениях.
— являются достаточными для реализации
рассматриваемой задачи в напряжениях.
В
пределе, когда v
= v'
и , фо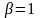 формулы (4.75) преобразуются в формулы
для изотропного упругого массива (4.50).
формулы (4.75) преобразуются в формулы
для изотропного упругого массива (4.50).
При
горизонтальном расположении плоскостей
напластования
 вид напряжений у поверхности скважины
аналогичен напряжениям для изотропного
массива:
вид напряжений у поверхности скважины
аналогичен напряжениям для изотропного
массива:
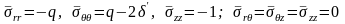 ,
,
где
 - приведенный коэффициент бокового
горного давления.
- приведенный коэффициент бокового
горного давления.
В этом случае интенсивность напряжений и среднее давление соответственно равны [см. формулы (4.51) и (4.52)]:
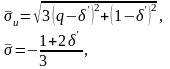
где
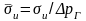 и
и
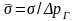 .
.
Для
большинства горных пород
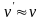 и
и
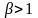 ,
т.е.
,
т.е.
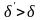 .
Поэтому из сравнения с формулами (4,51) и
(4.52) следует, что при
и
.
Поэтому из сравнения с формулами (4,51) и
(4.52) следует, что при
и
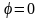 упругая анизотропия горных пород
приводит к росту величины
при
упругая анизотропия горных пород
приводит к росту величины
при
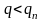 и к снижению
при
и к снижению
при
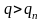 ,
где
,
где
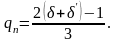
Среднее давление при этом увеличивается.
Как показали расчеты, выполненные по формулам (4.75) для , увеличение угла напластования приводит к неравномерному полю напряжений в приствольной зоне скважины, незначительному снижению интенсивности напряжений при и более значительному росту ее при . Среднее давление при этом убывает.
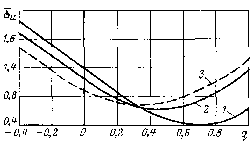
Рис.
65. Зависимость приведенной интенсивности
напряжений
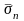 от
q
при
от
q
при
 :
:
1,
2 – соответственно при
и
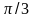 ,
3 – для изотропной породы при
,
3 – для изотропной породы при

На
рис. 65 показан пример зависимости
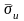 от q
и
для анизотропной горной породы. Там же
для сравнения показана зависимость
при
(изотропная порода). При этом величины
средних давлений
от q
и
для анизотропной горной породы. Там же
для сравнения показана зависимость
при
(изотропная порода). При этом величины
средних давлений
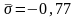 при
,
при
,
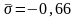 при
при
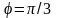 и
и
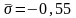 при
.
при
.
Если горная порода обладает только упругой анизотропией, но не прочностной, то, используя критерий прочности (4.17'), получим при необходимое условие устойчивости стенки скважины, аналогичное условию (4.53):
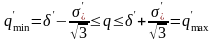 , (4.53`)
, (4.53`)
где
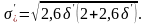
Допустимый диапазон изменения величины q, определяемый этим условием, шире, чем по условию (4.53), в основном за счет правостороннего ограничения.
При допустимый диапазон для q сужается, оставаясь, тем не менее, шире, чем по условию (4.53). Следовательно, если нет точных сведений о параметрах анизотропии, то, выбрав решение с помощью критерия (4.53), будем иметь некоторый запас прочности.
Для
горных пород, у которых величина
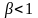 ,
с запасом прочности принимается условие
(4.53') независимо от угла напластования.
,
с запасом прочности принимается условие
(4.53') независимо от угла напластования.
Для
обеспечения длительной устойчивости
в условии (4.55) необходимо параметры
и
 ,
заменить на
,
заменить на
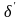 и
и
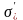 соответственно.
соответственно.
2.
Полученные решения (4.75) легко обобщить
на случай наклонно направленной скважины
(или интервала), ось которой составляет
произвольный угол
 с вертикалью [29].
с вертикалью [29].
Если направить ось oz основной системы координат xyz вдоль оси скважины и обозначить через угол между этой осью и нормалью к плоскости изотропии, то в расчетные формулы (4.75) достаточно ввести следующие изменения:
а)
вместо постоянных
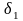 и
и
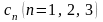 надо принять
надо принять

где
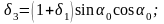
б)
в напряжения
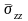 и
и
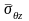 дополнить соответственно слагаемыми
дополнить соответственно слагаемыми
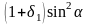 и
и
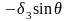 ;
;
в)
в формулах для определения констант
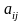 вместо
надо принять
.
вместо
надо принять
.
Если горная порода обладает явно выраженной анизотропией прочностных свойств, то для кратковременной устойчивости необходимо воспользоваться критерием прочности более общего вида.
Например,
приняв в (4.17) предположение, подобное
принятым в разд. 4.5, т. е.
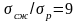 ,
,
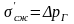 ,
получим
,
получим
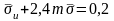 , (4.76)
, (4.76)
где
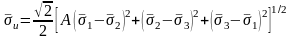 ;
;
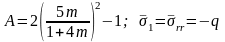 ;
;
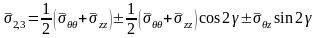 ;
;
 ,
,
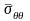 ,
и
приведенные к
,
и
приведенные к
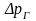 напряжения, определяемые по вышеприведенным
формулам при
.
напряжения, определяемые по вышеприведенным
формулам при
.
В частном случае для вертикальной скважины, пройденной в анизотропном горном массиве с горизонтальной плоскостью изотропии, получим обобщение в виде
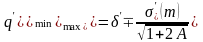 ,
,
где
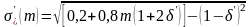 .
.
При отсутствии сведений о параметрах анизотропии горных пород, достаточно использовать формулы для изотропной модели, что обеспечит некоторый запас прочности и устойчивости стенки скважины.
Лекция 8. § Течения горных пород и пластовых флюидов
