§ 6. Задачи устойчивости горных пород в скважинах

На рис. 59 и 60 приведены диаграммы длительной устойчи­вости различных пород, которые позволили определить значения параметров долговечности. Для геологического разреза Лев­кинской площади получено: n = 3,5, A = 8,9 10^-10 при плотности глин p_r = 2.0 – 2.04 10³ кг/м³ и А = 3,3 10^-10 при p_r = 2.1 – 2.18-10³ кг/м³,

где напряжения принимали в МПа, время — в с. Для разреза Юбилейной площади получено: n = 2, A = 10^-9 при использовании глинистого раствора, обработанного УЩР, и А = 4,5-10^-10—для раствора, обработанного КС1. Приведем при­мер использования полученных моделей.

Пусть требуется найти минимально допустимую плотность ингибированного бурового раствора для вскрытия меловых отложений в интервале 3200—4000 м, если средняя плотность вышележащих пород р = 2500 кг/м³, δ= 0,5 и технологи­чески необходимое время от вскрытия до крепления интервала составляет Т= 6,4*10⁵с

Согласно (4 55) минимально допустимая плотность бурового раствора опреде­ляется по формуле

где к_а— коэффициент аномальности, Принимая во внимание опреде­ленные выше параметры А = 4,5 10^-10 и n = 2 для нормально уплотненной породы к_a = 1, найдем

и, так как Т/t₀ = 2, по вышеприведенной таблице находим q_min = 0,12 Поэтому

min p_c=1180 кг/м³

Если предположить, что с ростом коэффициента аномальности параметры А и n не изменяются, то при k_a=1,2, 1,4 и 1,6 получим соответственно

min p_с=1400, 1600 и 1800 кг/м³

2-(228)= Для упругопластичной модели примем как в задаче 1, справедливыми соотношения…….

Лекция 6. § Равновесие и движение твердых частиц в жидкости, газе и газожидкостной смеси

НЕОБХОДИМЫЕ И ДОСТАТОЧНЫЕ УСЛОВИЯ ОЧИСТКИ СТВОЛА СКВАЖИНЫ ОТ ШЛАМА. ОПРЕДЕЛЕНИЕ СКОРОСТИ ОСАЖДЕНИЯ ЧАСТИЦ

Одна из основных функций бурового раствора при бурении скважин - обеспечение выноса на дневную поверхность разрушен­ной на забое и осыпающейся со стенок породы (шлама). При этом качество очистки ствола скважины достигается надлежащим выбором режима промывки и свойств бурового раствора.

В настоящее время теоретическое решение этой задачи состоит в определении средней скорости потока в затрубном про­странстве из условия гидротранспорта шлама

где - скорость осаждения частицы шлама характерного размера l относительно несущей ее жидкости.

То есть считается, что достаточно определить величину ско­рости и задача выбора режима промывки с целью обеспечения качества очистки ствола будет решена. Поэтому не случайно отечественные и зарубежные исследователи на протяже­нии многих лет изучали и продолжают изучать именно проблему определения скорости . Она далека от своего решения, несмотря на целый ряд полученных аналитических, полуэмпирических, эмпирических зависимостей и большой объем экспериментального материала. Полученные результаты ограничены определенными условиями проведенных исследований и задачами, которые ста­вили перед собой авторы. Часто результаты различных авторов не сопоставимы или противоречивы [27]. Все это объясняется сложным характером движения частиц твердого тела в потоке жидкости и зависимостью этого движения от многих факторов.

1. Но прежде чем рассмотреть основные принципиальные моменты задачи определения скорости , оценим условие (2.148).

П о сути своей это условие не гарантирует качество очистки, так как не является достаточным критерием. Безусловно, превы­шение скорости потока над скоростью осаждения частиц необхо­димо. Но в какой мере? Некоторые авторы при ответе на данный вопрос, ссылаясь на результаты частного эксперимента А. С. Де­нисова, принимают условие выноса в виде

Однако справедливость этого условия в общем случае неправо­мерна. Истинная скорость жидкости в затрубном пространстве скважины изменяется по сечению от 0 до , а частицы шлама могут занимать любое положение. Поэтому ясно, что гарантиро­вать полный вынос шлама, поступающего в затрубное простран­ство, можно, если выполняется н еравенство

где - скорость жидкости в точке расположения центра частицы, определяемого координатой r.

Это возможно лишь при одном условии: каждая из ча­стиц шлама размером l расположена внутри ядра выноса границы которого являются корнями урав­нения

О днако специально поставленные во ВНИИКРнефти опыты свидетельствуют о том, что 100%-ного выноса шлама на дневную поверхность не бывает даже при развитом турбулентном режиме промывки [27]. Следовательно, частицы шлама могут занимать положение и вне ядра выноса. Так как ни детерминированной, ни стохастической закономерности расположения частиц в потоке не установлено, можно исходить из простого предположения: распо­ложение частицы шлама любого размера и формы в кольцевом сечении канала равновероятно. При этом допустимо считать, что концентрация частиц в затрубном пространстве весьма мала, т. е. каждую частицу шлама можно рассматривать независимо от других.

Тогда вероятность выноса любой частицы шлама разме­ром l, внесенной в затрубное пространство, будет равна отношению площади ядра выноса, определяемого уравнением (2.150), к площади S всего кольцевого сечения, т. е.

Д ля определения границ ядра и, следовательно, вероятности выноса частиц необходимо воспользоваться профилем ско­рости для кольцевого сечения скважины, используя формулы разд. 2.2.

Для упрощения расчетов допустимо заменить кольцевое сечение щелью шириной , где и - соответственно радиус трубы и скважины. Тогда, если в уравнении (2.150) воспользоваться профилем скорости для струк­турного режима течения неньютоновской жидкости Шведова — Бингама (2.30), из (2.151) легко получить

З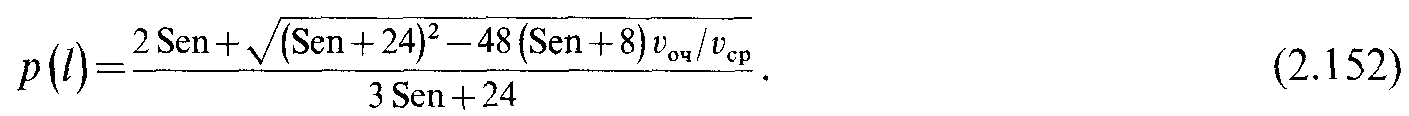 десь параметр Сен-Венана для кольцевого сече­ния; где - соответственно предельное напряжение сдвига и пластическая вязкость бурового раствора.

Отсюда, в частности, следует, что ненулевая вероятность выноса частицы размером l возможна при условии

П ри турбулентном режиме течения, используя профиль ско­рости, например, для гладких стенок канала (2.40), получим соответственно

и

где - параметр Рейнольдса для кольцевого сечения; - коэффициент гидравлического сопротивления.

Таким образом, условия (2.153) и (2.155), равно как и условие (2.148), являются лишь необходимыми условиями гидротранспор­та шлама, но не достаточными для обеспечения заданного уровня очистки ствола скважины от шлама.

Ф ормулы (2.152) и (2.154) определяют вероятность выноса частиц шлама заданного размера при заданном режиме промывки и свойствах бурового раствора, т. е решают прямую задачу. Для решения обратной задачи — определения параметров бурового раствора и необходимой подачи насосов можно исходить, например, из условия

для некоторого определенного максимального или среднего в выборке размера l частиц шлама. Тогда из формул (2.152) и (2.154) получим следующие необходимые и достаточные условия для гидротранспорта шлама:

о беспечивающие не менее чем 90%-ный уровень качества очистки ствола скважины соответственно при ламинарном и турбулентном режимах промывки.

Эти критерии обеспечат требуемое качество очистки ствола с избытком, если исходить из максимального размера частиц шлама, характерного при разрушении данной горной породы по заданной технологии бурения.

Легко заметить, что условия (2.155) и (2.158) приближаются к условиям (2.148) и (2.149), когда имеет место развитый турбулент­ный режим течения жидкости в затрубном пространстве скважины, т. е. когда .

Б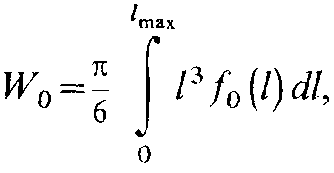 олее общий критерий качества очистки ствола скважины можно получить, если известен закон распределения размера частиц шлама, поступающих в затрубное пространство с забоя за некоторый промежуток времени . Тогда, принимая в качестве характерного размера l эквивалентный диаметр сферической частицы равного объема , можно вычислить объем всего поступившего в скважину шлама

где - объем частицы шлама.

О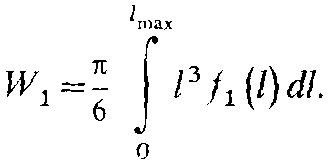 бозначив закон распределения частиц на устье, поступивших за время через , вынесенный объем шлама будет равен

В результате условие (2.156) можно заменить требованием

Е 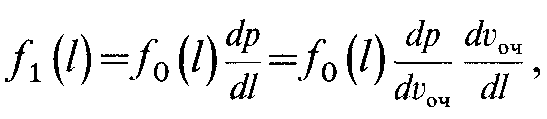сли исходить из того, что закон распределения частиц на устье зависит только от закона распределения частиц на забое и от вероятности их выноса, то, считая эти события независимыми, имеем

где определяется по формулам (2.152) или (2.154). Теорети­ческими и экспериментальными работами доказано, что при дроблении твердых тел распределение частиц по размерам подчиняется нормальному или логарифмически нормальному закону. Поэтому для расчета необходимо определить параметры закона распределения (математическое ожидание и дисперсию величины l) на забое, используя для этой цели исследование шлама, отобранного глубинными пробоотборниками или шламо-уловителями.

Д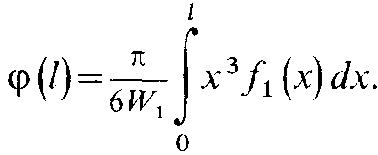 ля определения фракционного (гранулометрического) состава шлама, поступающего на устье, используется формула

Таким образом, для определения скорости и параметров бурового раствора необходимо в условие (2.156) или (2.159) подставить формулу скорости осаждения частицы заданного характерного размера и формы при условии обтекания ее жидкостью с соответствующими реологическими свойствами в ограниченном стенками гидравлическом канале.

Рассмотрим принципиальный подход к решению этой задачи.

2. Сила сопротивления, возникающая при движении частицы относительно жидкости, в общем случае определяется по формуле

г де - коэффициент сопротивления, который введен по аналогии с коэффициентом гидравлического сопротивления в формуле Дарси-Вейсбаха (см. разд. 2.2); - площадь сечения частицы, перпендикулярного к направлению ее движения (миделево сечение).

При установившемся движении частицы сила сопротивления должна быть уравновешена собственными весом частицы и выталкивающей силой, т. е. величиной

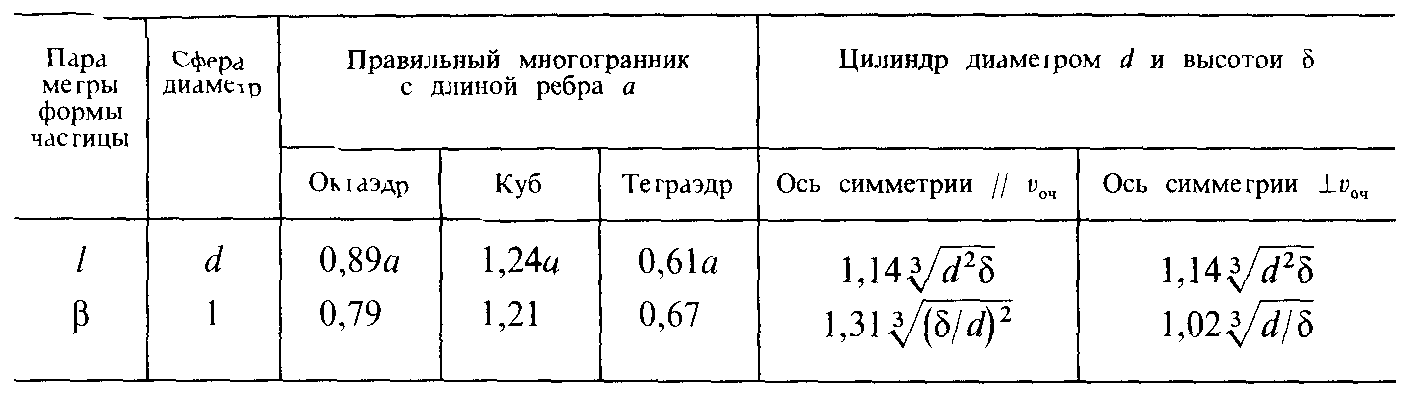
Т аблица 10

где g - ускорение силы тяжести; - соответственно плотности частицы и жидкости.

Поэтому из равенства следуют формулы

Приведенные формулы используются соответственно для вы­числения относительной скорости движения частицы по извест­ному коэффициенту сопротивления или для определения по экспериментальным значениям установившейся скорости осажде­ния частиц .

Величины l и для некоторых форм тел и ориентации относительно направления скорости приведены в табл. 10.

Сложность вычисления скорости осаждения частицы по фор­муле (2.162) состоит в том, что коэффициент сопротивления в общем случае функция многих детерминированных и случайных факторов, включая и искомую скорость .

Приближенную, но достаточно обоснованную зависимость для можно получить лишь на основе обобщения накопленного в настоящее время теоретического и экспериментального материала. Остановимся на наиболее важных результатах, позволяющих сделать полезные выводы для инженерного расчета.

Н аиболее проста и поэтому хорошо изучена задача осаждения частиц сферической формы в неограниченном объеме, заполнен­ном ньютоновской жидкостью [3]. На основе многочисленных опытных данных установлено, что коэффициент сопротивления зависит от параметра Рейнольдса

по закону, представленному графиком на рис. 22 (кривая l). Характерной особенностью этой кривой является плавность

п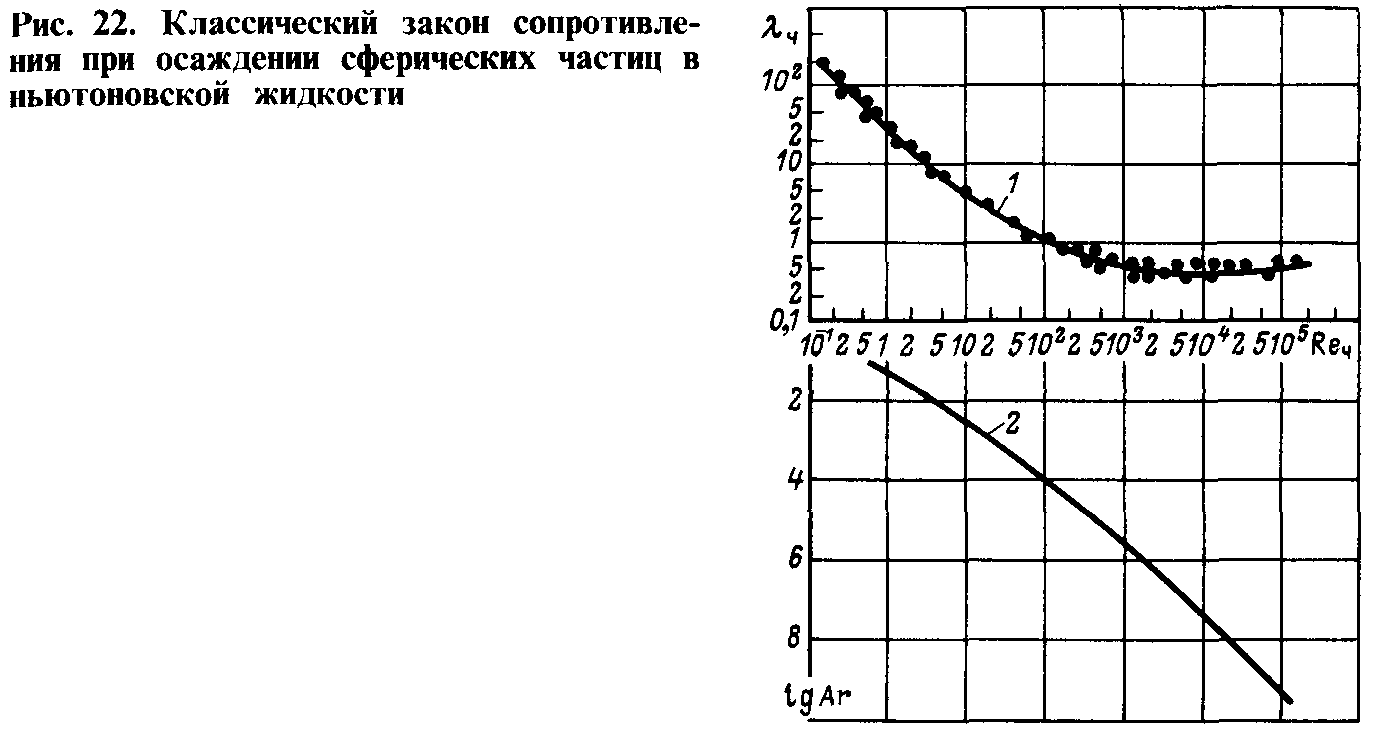 ерехода от ламинарного (при ) к развитому турбулентному (при ) обтеканию частицы. Область назы­вается переходной или промежуточной.

Если в (2.164) подставить (2.162), то получим полезное соотношение

г де - параметр Архимеда.

При медленном осаждении сферической частицы, когда силы вязкости значительно превосходят силы инерции, т. е. при , удалось получить простое аналитическое решение в виде следующих эквивалентных соотношений:

Э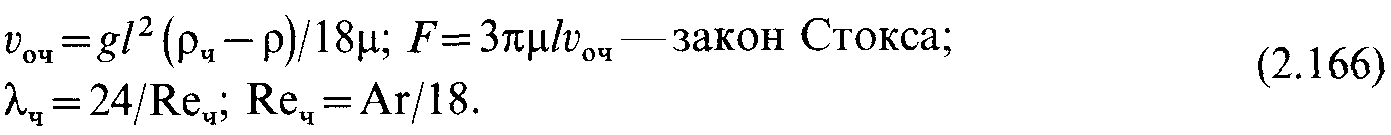 то решение хорошо согласуется с данными опытов вплоть до значения .

В турбулентной области коэффициент практически не зависит от параметра , и его можно считать постоянным

В этой области, которую принято называть областью действия закона Ньютона, сила сопротивления (2.160) пропорциональна квадрату скорости , которая согласно (2.162) и (2.167) вычис­ляется по формуле Риттингера

г де

В этом случае из соотношения (2.165) имеем

и поэтому условие соответствует условию .

Для переходной области ( или ) удалось получить несколько вполне удовлетворительных аппрок­симаций опытной кривой l на рис. 22. Одна из наиболее удачных - аппроксимация, предложенная Л. М. Левиным [6]

к оторая совместно с формулой (2.165) приводит к уравнению относительно искомого параметра Рейнольдса:

Е сли левую часть уравнения (2.170) представить кривой 2 на рис. 22, то по заданному легко находится . Можно воспользоваться неплохой аппроксимацией этой кривой, предло­женной Р. Б. Розенбаум и О. М. Тодес [6],

О тметим важное обстоятельство: по конструктивному содер­жанию формула (2.169) представляет собой простое сращивание двух асимптотических решений (2.166) и (2.167). Так как этот прием оказался результативным в рассмотренной задаче, то в качестве рабочей гипотезы примем ниже, что он допустим и для более общей задачи осаждения частицы произвольной формы в ньютоновской или неньютоновской жидкости в трубе или затрубном пространстве.

В общем случае медленного обтекания частицы ( ) жидкостью Шведова - Бингама силу сопротивления можно пред­ставить в виде

г де - коэффициент влияния формы частицы и стенок канала при ламинарном обтекании; - коэффициент пропорциональ­ности.

Вообще говоря, параметры и можно считать неопределен­ными, если ставится задача получения наилучшего согласования опытных данных и модели. Но для инженерных расчетов можно принять следующие известные результаты [39]:

п ри падении частиц в круглой трубе

п ри падении частиц в плоской трубе или кольцевом канале

где - параметр, учитывающий влияние формы частицы и ее ориентации относительно направления осаждения; - соот­ветственно диаметр трубы и ширина кольцевого зазора.

Для тел, близких к правильным многогранникам (куб, октаэдр и т. д.), . Без большой погрешности можно принять и для дископодобных, цилиндрических и иглоподобных частиц, когда . Здесь - соответственно высота и диаметр частицы.

П ри параметр определяется по формулам:

е сли ось симметрии совпадает с направлением осаждения частицы, и

если ось симметрии перпендикулярна к направлению осаждения частицы.

П ри параметр определяется по формулам:

если ось симметрии совпадает с направлением осаждения части­цы, и

е сли ось симметрии перпендикулярна к направлению осаждения частицы.

По данным Р. И. Шищенко, коэффициент . Далее будем считать, что .

С равнивая правые части формул (2.160) и (2.161) с (2.172), получим соответственно.

где - параметр Хедстрема для части­цы. После умножения обеих частей (2.174) на получим

г де ; при частица не тонет.

Таким образом, формулы (2.172) — (2.175) являются обобще­нием формул (2.166).

П ри турбулентном режиме обтекания частиц рекомендуется обобщенная формула Риттингера

где - коэффициент влияния формы и стенок канала при турбулентном обтекании. Эта формула эквивалентна соотно­шению

Д ля коэффициента влияния предложено несколько эмпири­ческих зависимостей, из которых наиболее удачной признают формулу Р. Ф. Уханова [27], которая в наших обозначениях имеет вид

С ращивая асимптотические решения (2.173) и (2.176), получим формулу для переходной области

После подстановки этой формулы в (2.165) получим уравнение относительно искомой величины :

Б лагодаря сходству уравнений (2.171) и (2.178), примем по аналогии с (2.171) допустимость следующей аппроксимации решение уравнения (2.178)

А декватность этой теоретической модели опытным данным, представленным в работе [38], показана в табл. 11.

О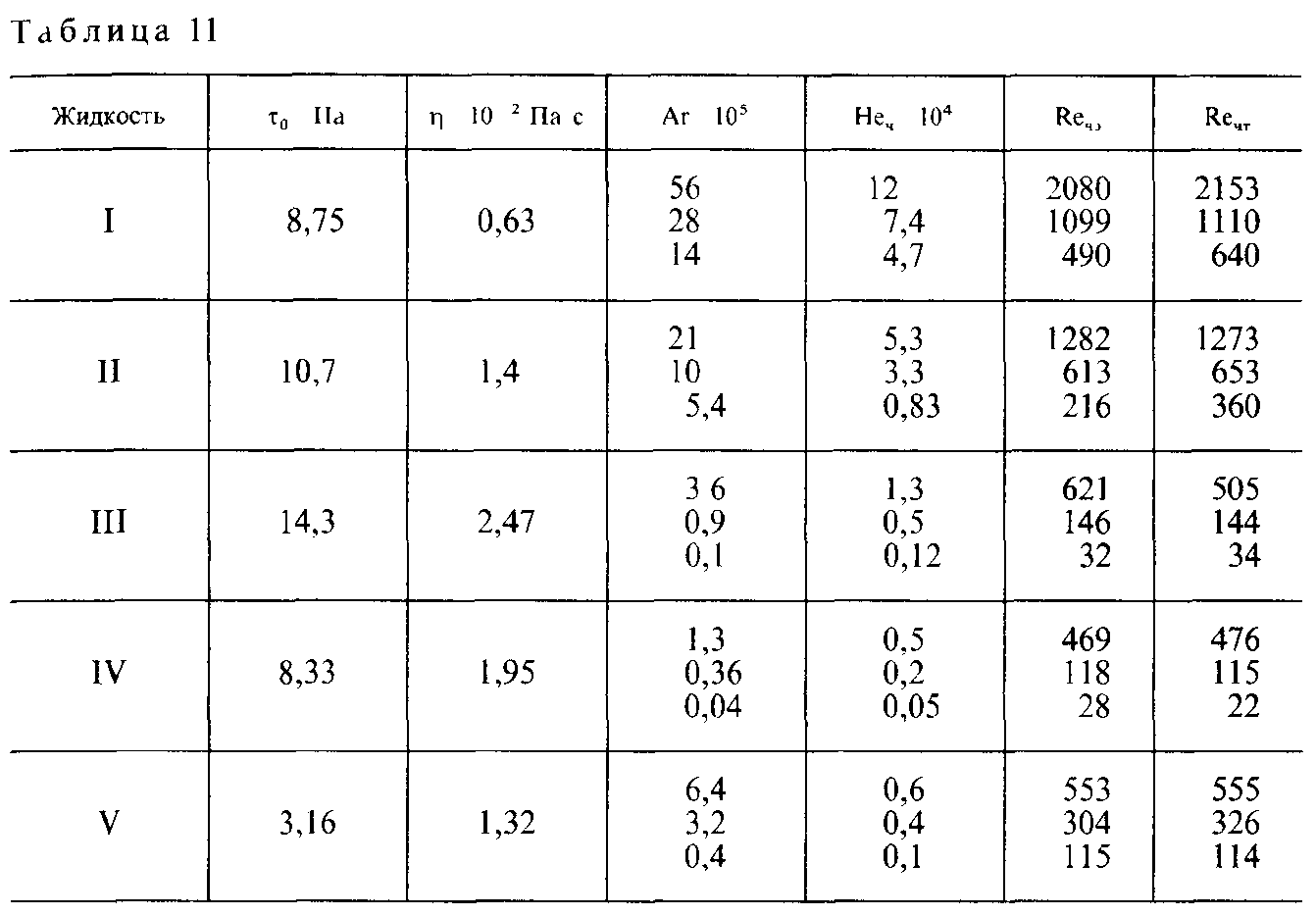 пыты проводились в стеклянной трубке диаметром и длиной . Жидкость, основу которой со­ставляла карбоксиметилцеллюлоза, имела плотность .

Варьируя реологические параметры, размеры частиц и их плот­ность, авторы обеспечили обтекание частиц при всех режимах. Частицы имели форму дисков, и при их падении фиксировались два направления ориентации: плоскостью (ось симметрии парал­лельна направлению осаждения) и ребром (ось симметрии перпендикулярна к направлению осаждения). Наиболее пред­ставительными были данные по оседанию частиц плоскостью, которые и показаны в табл 10 для пяти типов жидкостей Как видно, получено вполне удовлетворительное соответствие между опытными значениями и теоретическими . При осаждении частиц ребром такого соответствия не полу­чилось.

Это не случайный результат. Он объясняется тем, что эмпирическая формула (2.179) получена при изучении выноса частиц в турбулентном потоке. Но в работе [47] показано, что в турбулентном потоке дископодобные частицы ориентируются плоскостью. Поэтому формула не может быть справедливой при другой ориентации таких частиц.

Не соответствует опытным данным [38] и рекомендуемая Ульямсом и Бруком формула для осаждения частиц ребром. Она дает весьма завышенные значения скорости по срав­нению с опытными данными. Кстати, это отмечено и в дру­гих работах. Для получения эмпирического коэффициента при осаждении частиц ребром числа опытных данных недо­статочно.

Таким образом, согласно полученным выше результатам, выбор режима промывки, обеспечивающего качественную очистку ствола скважины, сводится к следующей расчетной схеме.

Параметр , вычисленный по формуле (2 179), сравнивается с критическим параметром

г де и диаметр скважины и наружный диаметр бурильной трубы, критическое значение параметра Рейнольдса, кото­рое при вычисляется по формуле

- параметр Хедстрема для кольцевого сечения. Если , то качественная очистка ствола скважины возможна при ламинарном режиме течения бурового раствора в затрубном пространстве скважины, и поэтому согласно условию (2.157) имеем

П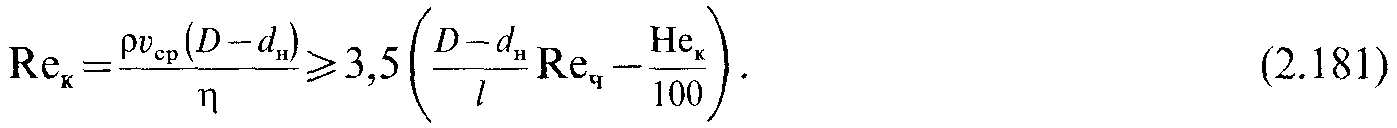 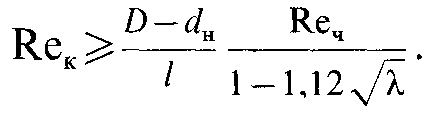ри в затрубном пространстве необходимо создать турбулентный режим, удовлетворяющий условию [см формулу (2 158)]

Пусть, например, требуется определить минимальную подачу насосов при промывке скважины диаметром , если диаметр бурильных труб , параметры бурового раствора , , с, характерный размер частиц шлама , форма частиц близка к правильному многограннику (т.е. ), плотность .

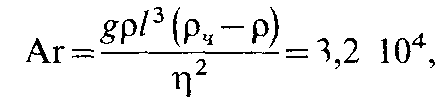
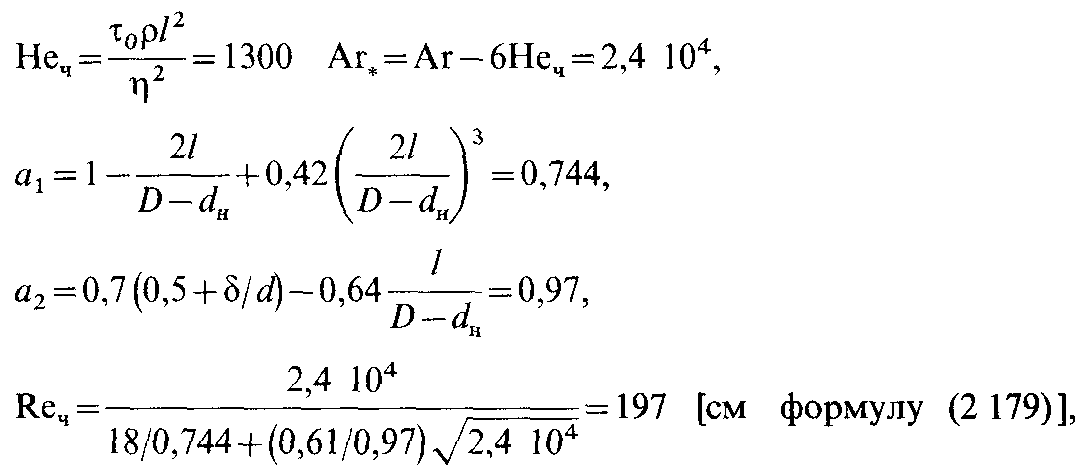
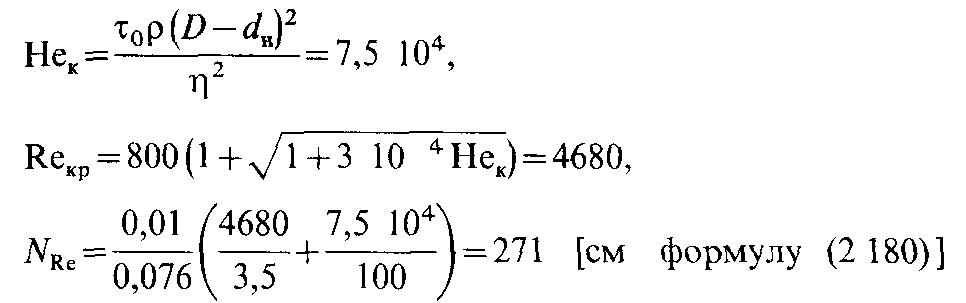Приведем последовательность расчета

Так как , то, используя формулу (2 181), определим минимально необходимую величину расхода

При этом средняя скорость течения раствора в затрубном пространстве скважины составит , а относительная скорость осаждения частицы . Поэтому минимально необходимое время на промывку скважины, например, глубиной составит .

П одачу насосов можно увеличить до некоторого допустимого значения , определяемого допустимой величиной изменения забойного давления Если

то величина вычисляется по формуле для структурного режима, в противном случае - по формуле для турбулентного режима течения (см. разд. 2.2)

Лекция 7. § Установившиеся и неустановившиеся процессы

(4-5) БАЗОВЫЕ ЗАДАЧИ УСТОЙЧИВОСТИ ГОРНЫХ ПОРОД В СКВАЖИНАХ

Простейшие (базовые) решения задач о напряженном состоя­нии и устойчивости горных пород в скважинах получены при следующих допущениях:

а) начальное (до бурения скважины) напряженное состояние горного массива определяется гравитационной силой , поровым давлением р_п(z) и условием нулевого смещения в горизонтальной плоскости ху ( ),

т. е. следующими эффективными напряжениями:

и при (4.43)

где , —средняя плотность вышележащих пород, z — рассматриваемая глубина, δ = v/(1-v)—коэффициент боково­го горного давления;

б) горная порода — это однородное изотропное упругое, упругопластичное или вязкопластичное твердое тело типа глин и солей;

в) скважина—это полубесконечная, круглая вертикальная ци­линдрическая полость в горном массиве, заполненная жидкостью плотностью р_с;

г) инерционные силы ра₁, пренебрежимо малы, т. е. горные породы в стационарном или квазистационарном состоянии.

В силу этих допущений напряженно-деформированное состоя­ние приствольной зоны скважины будет характеризоваться осевой симметрией и равенством нулю напряжений и деформаций сдвига ( при ), если выбрана цилиндрическая система координат к, θz с осью z, направленной вдоль оси скважины.

Нормальные эффективные напряжения σ_u и перемещения и, можно представит виде

(4.44)

где и — дополнительные эффективные напряжения и радиальное перемещение, обусловленные образованием скважины. В (4.44) принято, что дополнительное осевое перемещение равно нулю, т. е.

= 0. (4.45)

Поэтому относительно дополнительных величин , и (4.46)

имеем задачу о плоской деформации.

Напряжения должны удовлетворять следующим уравне­ниям равновесия

(4.47)

Согласно условию в) и формулам (4.43) — (4.45) — граничным условиям

при r = Rс и = 0 при , (4.48)

где , Rс — радиус скважины