
- •Кинематика сплошной среды
- •Элементы теории деформаций
- •Динамические величины и элементы теории напряжений
- •Раздел 2. (4) Уравнения механики сплошных сред
- •§ 1. Уравнение неразрывности
- •§ 2. Уравнения движения и равновесия
- •§ 3. Уравнения состояния (математические модели)
- •§ 1. Уравнение неразрывности
- •§ 2. Уравнения движения и равновесия
- •Уравнением моментов
- •§ 3. Уравнения состояния (математические модели)
- •§ 4. Уравнения состояния гидромеханики
- •§ 5. Основные уравнения теории фильтрации
- •§ 5.1 Линейные уравнения и граничные задачи фильтрации.
- •§ 6. Мгновенные уравнения состояния и критерии прочности
- •§ 7. Временные уравнения состояния и критерии длительной прочности
- •§ 8. Общая система уравнений механики деформируемого твердого тела
- •Задачи гидромеханики в бурении
- •§ 1. Базовые задачи гидродинамики при промывке и цементировании скважин
- •§ 2. Ламинарное и турбулентное течение жидкостей в щелевом канале
- •§ 3. Ламинарное и турбулентное течение жидкостей в кольцевом канале
- •§ 4. Задачи фильтрации при строительстве скважин
- •Формула дюпюи и ее обобщения
- •§1. Среды в механике сплошной среды
- •§2. Горные породы
- •§ 3. Критерии разрушения сред на основе теории трещин
- •§ 4. Порода - деформируемое твердое тело
- •§ 5. Реологические свойства
- •§ 6. Задачи устойчивости горных пород в скважинах
- •Напряженное состояние и устойчивость анизотропных пород в вертикальных и наклонных скважинах
- •4.10. Определение горного давления на крепь ствола скважины
- •4.11. Центрирование бурильных и обсадных колонн.
§ 3. Критерии разрушения сред на основе теории трещин
Известно,
что реальная прочность твердых тел во
много раз меньше теоретической, равной
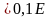 ,
где Е
– модель Юнга. Объясняется это тем, что
реальные тела имеют разного рода микро-
и макродефекты: трещины, поры, узкие
полости, инородные включения и т.п.
Распределение этих дефектов в объеме
тела, как правило, случайно, и поэтому
случайна величина прочности материала.
Экспериментально это убедительно
подтверждается тем, что наблюдается
разброс (иногда довольно значительный)
при испытаниях одинаковых образцов в
одинаковых условиях, и имеет место так
называемый масштабный эффект: большие
образцы имеют меньшую прочность чем
малые образцы той же формы. Это характерно
для всех хрупких тел вообще, горных
пород и тампонажного камня в частности.
,
где Е
– модель Юнга. Объясняется это тем, что
реальные тела имеют разного рода микро-
и макродефекты: трещины, поры, узкие
полости, инородные включения и т.п.
Распределение этих дефектов в объеме
тела, как правило, случайно, и поэтому
случайна величина прочности материала.
Экспериментально это убедительно
подтверждается тем, что наблюдается
разброс (иногда довольно значительный)
при испытаниях одинаковых образцов в
одинаковых условиях, и имеет место так
называемый масштабный эффект: большие
образцы имеют меньшую прочность чем
малые образцы той же формы. Это характерно
для всех хрупких тел вообще, горных
пород и тампонажного камня в частности.
Кроме того, современные экспериментальные данные свидетельствуют о постепенном развитии разрушения и о большой роли первичных дефектов в формировании картины разрушения. Трещины начинаются развивается задолго до полного разрушения тела. Разрушение не единовременный акт, оно развивается с большей или меньшей скоростью при сравнительно невысоких напряжениях и представляет собой некоторый динамический процесс (см. лекцию 2).
Поэтому прежние представления о наступлении разрушения при достижении некоторого критического напряжения материала устарели.
Для оценки реальной прочности тел необходимо исходить из наличия в теле дефектов. При этом важное значение приобретает использование современных результатов теории трещин. Хотя эти результаты не позволяют охватить все многообразие особенностей разрушения, но их использование дает инженеру необходимый инструмент для более правильной оценки прочности тел и для более глубокого понимания причин разрушения. С помощью теории трещин можно количественно объяснить больше различие между реальной и теоретической прочностью тел, влияние масштабного фактора, различие между прочностью на сжатие и растяжение и многое другое.

Рис. 29. Трещина в поле равномерного растяжения при плоской деформации
Гриффитс впервые показал, что низкая реальная прочность хрупких тел вызывается наличием трещин, приводящих к значительной концентрации напряжений. В основе теории Гриффитса лежит представление об энергетическом барьере – поверхностной энергии, который необходимо преодолеть для развития трещины, т.е. для образования новой поверхности. В то же время при увеличении трещины освобождается потенциальная энергия, которая может быть израсходована на разрушение.
Любой материал в данных условиях (температура, влажность, внешняя среда и т.д.) характеризуется некоторой плотностью поверхностной энергии , которая определяет величину работы, необходимую для образования единицы новой свободной поверхности. Энергетический критерий Гриффитса формулируется следующим образом: разрушение тела развивается, если плотность освобождающейся энергии достигает критического значения. Например, для трещины длиной 2l в поле равномерно растяжения напряжением p в условиях плоской деформации (рис. 29) критерий Гриффитса записывается в виде
 ,
,
где
 -
потенциальная энергия тела.
-
потенциальная энергия тела.
Отсюда следует условие предельного равновесия при растяжении
 .
(4.1)
.
(4.1)
Если
при данной длине трещины напряжение
 ,
то трещина не растет. Если же напряжение
достигает критического значения
,
то трещина не растет. Если же напряжение
достигает критического значения
 ,
то трещина расширяется. Из формулы (4.1)
вытекает, что не предельное напряжение
-
прочностная характеристика материала,
а произведение
,
то трещина расширяется. Из формулы (4.1)
вытекает, что не предельное напряжение
-
прочностная характеристика материала,
а произведение
 .
(4.2)
.
(4.2)
В инженерных расчетах используется более удобный силовой критерий прочности Ирвина, который по существу эквивалентен критерию Гриффитса, но основан на особенности распределения напряжений в окрестности вершины трещины:
 ,
,
где r, - локальная система координат с началом в вершине трещины, k – коэффициент интенсивности напряжений (КИН), который зависит от формы тела, системы нагрузок и геометрии трещины.
Согласно
критерию Ирвина, для каждого материала
есть критическое значение коэффициента
интенсивности напряжений
 ,
по достижении которого трещина начинает
расти, т.е. для прочности тела необходимо,
чтобы
,
по достижении которого трещина начинает
расти, т.е. для прочности тела необходимо,
чтобы
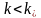 .
.
Таким образом, для оценки влияния трещин на прочность тела необходимо решить соответствующую задачу теории упругости, найти КИН и сравнить его с опытной для данного материала величиной .

Рис. 30. Три типа трещин: стрелками показано направление перемещения
Обычно для описания возможного поведения трещины используют понятия о трех типах ее раскрытия (рис. 30):
а) нормальный отрыв (тип I) – перемещения берегов трещины перпендикулярны к ее плоскости;
б) поперечный сдвиг (тип II) – перемещения берегов происходят в плоскости трещины перпендикулярно к ее фронтальной линии;
в) продольный сдвиг (тип III) – перемещения берегов совпадают с плоскостью трещины и параллельны ее направляющей кромке.
Напряжения
и перемещения около вершины трещины
для каждого типа раскрытия определяются
коэффициентами интенсивности
 и
и
 нормального напряжения, поперечного и
продольного сдвигов соответственно.
Иногда в литературе используют другие
обозначения КИН
нормального напряжения, поперечного и
продольного сдвигов соответственно.
Иногда в литературе используют другие
обозначения КИН
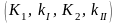 и вводят иные физические понятия.
Например, согласно Г.И. Баренблатту,
и вводят иные физические понятия.
Например, согласно Г.И. Баренблатту,
 называют модулем сцепления, а
называют модулем сцепления, а
 -
сдвиговым модулем сцепления.
-
сдвиговым модулем сцепления.
В простейших случаях равномерного растяжения плоскости (рис. 29) плоского и антиплоского сдвигов (рис. 31) коэффициенты интенсивности напряжений вычисляются по формулам
 ,
,
где
 -
соответственно силы растяжения, плоского
и антиплоского сдвигов.
-
соответственно силы растяжения, плоского
и антиплоского сдвигов.

Рис. 31. Трещина в поле сдвига
а – плоского, б - антиплоского
Для
приложений наибольший интерес представляют
раскрытия трещин типа I
и II
в условиях плоской деформации
 или плоского напряженного состояния
или плоского напряженного состояния
 ,
для которых хорошо разработаны методы
теоретического вычисления коэффициентов
и
сформулирован удовлетворительный
критерий разрушения: трещина развивается
по направлению наибольшего растягивающего
напряжения, если выполняется условие
,
для которых хорошо разработаны методы
теоретического вычисления коэффициентов
и
сформулирован удовлетворительный
критерий разрушения: трещина развивается
по направлению наибольшего растягивающего
напряжения, если выполняется условие
 ,
(4.3)
,
(4.3)
где
 - угол начального распространения
трещины относительно ее направления
(ориентации).
- угол начального распространения
трещины относительно ее направления
(ориентации).

Рис. 32. Предельные характеристики тела с трещиной при равномерном растяжении
Отсюда и находятся критические значения внешней нагрузки, при которой начинается локальное разрушение тела. Например, при равномерном растяжении или сжатии плоскости с трещиной, расположенной под углом к направлению внешней силы, имеют место следующие формулы для определения:
Коэффициентов интенсивности напряжений
 ;
;
угла начального распространения трещины
 .
.
Предельного напряжения
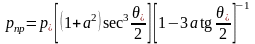 ,
,
где
верхние знаки соответствуют растяжению,
а нижние – сжатию;
 -критическое
значение напряжения при растяжении
плоскости с трещиной, перпендикулярной
к направлению растяжения [см. рис. 29 и
формулу (4.1)].
-критическое
значение напряжения при растяжении
плоскости с трещиной, перпендикулярной
к направлению растяжения [см. рис. 29 и
формулу (4.1)].
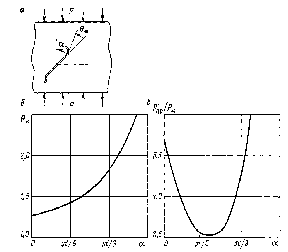
Рис. 33. Предельные характеристики тела с трещиной при равномерном сжатии
Отсюда следует известный экспериментальный факт: для всех хрупких тел предельное сжимающее напряжение значительно выше растягивающего предельного напряжения. Если обратить внимание на зависимость предельных напряжений от ориентации трещины и ее длины, то станет ясна причина и другого экспериментального факта: сильного разброса предела прочности для хрупкого тела.

Рис. 34. Основные виды испытаний образцов с имитированными трещинами (надрезами) при:
а – растяжении, б – изгибе
Поэтому величина считается более стабильной прочностной характеристикой. Для ее определения проводятся испытания образцов с трещинами или имитирующими их острыми надрезами согласно существующим методиками. Чаще всего опыты осуществляются в условиях плоского напряженного или плоского деформированного состояния, когда образцы испытываются на растяжение или изгиб, например как показано на рис. 34.
Коэффициенты интенсивности напряжений при указанных на рис. 34 видах нагружения вычисляются по формуле
 ,
,
где

если
 -
малая величина то достаточно ограничиться
двумя слагаемыми. Повышая уровень
нагрузки (р
или Q)
и наблюдая одновременно за продвижением
трещины, устанавливают для данного
образца при определенных условиях опыта
(температура, среда и т.д.) критическое
значение р
или Q
и, следовательно, значение критического
коэффициента интенсивности
.
-
малая величина то достаточно ограничиться
двумя слагаемыми. Повышая уровень
нагрузки (р
или Q)
и наблюдая одновременно за продвижением
трещины, устанавливают для данного
образца при определенных условиях опыта
(температура, среда и т.д.) критическое
значение р
или Q
и, следовательно, значение критического
коэффициента интенсивности
.

Рис. 35 Характерный график трещиностойкости тел в агрессивных средах
Опытные данные свидетельствуют о том, что с ростом температуры растет сопротивление тел хрупкому расширению, а с ростом влажности оно падает. Испытания образцов с трещинами в агрессивной среде позволяют выделить существенную роль среды в изменении трещиностойкости. В таких опытах фиксируется время до разрушения при определенных начальных значениях коэффициента интенсивности напряжений . На рис. 35 показана опытная кривая, построенная по взятым значениям . Чем ближе к критическому значению , тем меньше время до разрушения. Опытная кривая, как правило, имеет горизонтальную асимптоту (пунктир), соответствующую так называемому пределу коррозионной прочности.
Таким
образом, при воздействии среды и
достаточно высоких напряжениях имеющиеся
на теле трещины «подрастают» с течением
времени. Отношение
 характеризует ресурс прочности, т.е.
определяет время до разрушения.
Аналогичным образом трещины «подрастают»
до критического состояния и при
циклических нагрузках. В литературе
изложено несколько вариантов уравнения,
описывающего рост усталостных трещин.
характеризует ресурс прочности, т.е.
определяет время до разрушения.
Аналогичным образом трещины «подрастают»
до критического состояния и при
циклических нагрузках. В литературе
изложено несколько вариантов уравнения,
описывающего рост усталостных трещин.
Предлагается кинетическое уравнение вида
 ,
,
где
l
– длина трещины; N
– число циклов;
 -
изменение коэффициента интенсивности
напряжений в цикле; п
– константа материала. Множитель с
зависит от свойств материала, частоты
и среднего напряжения. Согласно этому
уравнению, скорость роста трещины быстро
увеличивается с приближением к
разрушающему числу циклов.
-
изменение коэффициента интенсивности
напряжений в цикле; п
– константа материала. Множитель с
зависит от свойств материала, частоты
и среднего напряжения. Согласно этому
уравнению, скорость роста трещины быстро
увеличивается с приближением к
разрушающему числу циклов.
Если результаты испытаний на прочность номинально идентичных образцов при номинально идентичных условиях нагружения колеблются в широких пределах, то, очевидно, значимость среднего значения прочности тела довольно сомнительна. При этом вряд ли можно оперировать средними значениями. Необходимо сам разброс рассматривать как существенную физическую особенность процесса. В первую очередь это относится к хрупкому разрушению и длительной прочности, для которых ширина разброса может превышать среднее значение соответствующих предельных величин.
Для описания разброса наиболее эффективны статистические методы, опирающиеся на прямые экспериментальные данные и простейшие формальные вероятностные модели. Статистический подход позволяет установить закономерности влияния размеров тела, характера нагружения, распределения напряжений и других факторов. Работы в этом направлении ведутся давно и составляют важное направление в проблеме разрушения. Здесь достаточно коснуться лишь некоторых основных моментов.
Для статистического описания хрупкого разрушения предложены три модели, каждая из которых приводит к своей функции распределения: нормальное распределение, гамма-распределение и третье асимптоматическое распределение наименьших значений. Хотя аналитические выражения для этих трех функций совершенно различны, они не всегда легко различимы при использовании небольшого числа данных.поэтому в большинстве случаев ограничиваются третьим асимптотическим распределением наименьших значений, которое следует из модели наислабейшего звена: разрушение образца в целом определяется локальной прочностью его наиболее слабого элемента объема.
Функция
распределения прочности
 при хрупком разрушении представляется
следующим образом:
при хрупком разрушении представляется
следующим образом:
 (4.4)
(4.4)
где
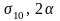 -
параметры закона распределения,
подлежащие определению из опытов.
-
параметры закона распределения,
подлежащие определению из опытов.
Последнее выражение с помощью двукратного логарифмирования можно преобразить в уравнение прямой
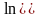
в
координатах
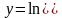 и
и
 .
Обычно для построения прямой
.
Обычно для построения прямой
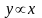 используются
абсциссы
используются
абсциссы
 и соответствующие им ординаты
и соответствующие им ординаты
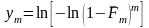 ,
где
,
где
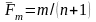 ;
т
– номер наблюдаемого значения прочности
(расположены в порядке возрастания); п
– общее число наблюдений.
;
т
– номер наблюдаемого значения прочности
(расположены в порядке возрастания); п
– общее число наблюдений.
Для
определения параметров
 и
и
 используется либо графическое построение,
либо метод наименьших квадратов. В
результате
используется либо графическое построение,
либо метод наименьших квадратов. В
результате
 ,
,
где
 - значение х
при у
= 0.
- значение х
при у
= 0.
Доказано,
что параметр
связан с объемом тела. Если найден
параметр
 для образца объемом
для образца объемом
 ,
то для образца объемом
,
то для образца объемом
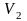 будет
будет
 .
.
Вероятность разрушения образца под действием напряжения вычисляется по формуле
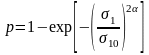 ,
,
где
отношение
 можно рассматривать как коэффициент
безопасности.
можно рассматривать как коэффициент
безопасности.
Отсюда
легко доказать, что для двух образцов,
объемы которых
и
![]() ,
разрушение равновероятно, если выполняется
соотношение
,
разрушение равновероятно, если выполняется
соотношение
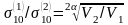 .
.
В общем случае результаты испытаний на прочность могут быть приближены одним уравнением (4.36) лишь в довольно ограниченном интервале. Чаще для адекватного описания требуются две прямые с различным наклоном. Точка пересечения этих прямых может означать изменение самого механизма разрушения.
Для того, чтобы определить влияние на хрупкое разрушение неоднородного поля напряжений, сравнивают наибольшее напряжение в неоднородном поле напряжений в момент разрушения с разрушающим напряжением в однородном поле, используя условие равной вероятности разрушения.
Например, в случае чистого изгиба балки имеет место следующее соотношение между прочностью на изгиб и прочностью на растяжение:
 ,
,
где
V
– объем образца, испытываемого на
растяжение;
 - объем балки. Если, например,
- объем балки. Если, например,
 и
и
 ,
то
,
то
 .
.
Статистический
подход к хрупкому разрушению при
трехмерном напряженном состоянии может
быть основан на допущении, что по
отношению к разрушению напряжения
 не взаимодействуют. Тогда сравнение с
вероятностью разрушения под действием
одноосного нагружения напряжением
дает уравнение равной вероятности
разрушения
не взаимодействуют. Тогда сравнение с
вероятностью разрушения под действием
одноосного нагружения напряжением
дает уравнение равной вероятности
разрушения
 ,
,
представляющее собой условие трехмерного разрушения.
Лекция 5. Напряженное и деформированное состояние системы «скважина-пласт»
(4-1) § 1 МГНОВЕННЫЕ УРАВНЕНИЯ СОСТОЯНИЯ И КРИТЕРИИ ПРОЧНОСТИ
 (5.1)
(5.1)
 (5.2)
(5.2)
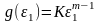 (5.3)
(5.3)
 (5.4)
(5.4)
 (5.5)
(5.5)
1. В практике инженерных расчетов чаще других используется следующая эмпирическая зависимость предельного значения ( или ) от среднего нормального напряжения , предложенная Э. Хоеком:
 ,
(5.6)
,
(5.6)
где с – значение при ; a, b – константы, являющиеся функциями температуры, влажности и др.
Для многих горных пород хорошей аппроксимацией может оказаться линейная зависимость, называемая критерием Мора,
(5.7)
Инженерные расчеты удобно проводить, когда зависимость параметров с, а, b, равно как и K и т в формуле (5.3), от температуры и влажности принята в аналитической форме. Однако таких общепринятых норм в литературе не предложено. Поэтому необходимо руководствоваться соображениями удобства при расчетах с требуемой точностью. Например, в формуле (5.3) часто бывает удобным фиксировать показатель т, а коэффициент K считать линейной функцией, или экспонентой.
2. При сложно-напряженном состоянии упругое деформирование изотропных тел описывается общими уравнениями состояния, называемыми обобщенным законом Гука:
(5.8)
т.е. компоненты девиаторов напряжений и деформаций, среднее нормальное напряжение и относительное изменение объема пропорциональны или в эквивалентной форме:
(5.9)
т.е. компоненты тензора напряжений суть линейные функции компонент тензора деформаций и обратно:
(5.10)
где - модуль сдвига; - коэффициент Ламе. Характерно, что коэффициенты пропорциональности в этих общих уравнения определяют параметрами, получаемым при простых видах нагружения.
На основании уравнений (5.8) и формул (1.21), (1.40) выведено полезное соотношение
 ,
(5.8/)
,
(5.8/)
т.е. интенсивность касательных напряжений Т пропорциональна интенсивности деформаций сдвига Г.
Более сложными уравнениями описывается неупругая деформация. В приложениях обычно пользуются упрощенными теориями пластичности.
Наиболее широкое применение получили уравнения состояния деформационной теории пластичности
(5.11)
или в эквивалентной форме
, (5.12)
и обратная зависимость
, (5.13)
которые являются простым обобщением уравнений (5.8) – (5.10).
В
уравнениях (5.11) – (5.13) функция g(Г)
в силу соотношения
 и формулы (5.2) определяется по виду
функции
,
например, подобно формуле (5.3):
и формулы (5.2) определяется по виду
функции
,
например, подобно формуле (5.3):
 .
.
Функция
 служит коэффициентом в обратном
соотношении
служит коэффициентом в обратном
соотношении
 :
например, для степенного закона (5.3)
:
например, для степенного закона (5.3)
 ,
,
где .
В случае несжимаемого тела (v = 0,5) уравнения состояния принимают вид
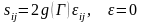 .
.
В состояния пластического течения (см. рис.42 участок АВ), например, при обобщенном критерии Губера – Мизеса, характеризующим переход к пластическим деформациям,
 ,
,
3. Условие перехода какого-либо элемента нагруженного твердого тела в состояние хрупкого разрушения или пластического течения, когда в известной мере исчерпывается несущая способность, принято называть критерием прочности при кратковременном монотонном нагружении.
Поэтому в общем случае критерий прочности определяется некоторой предельной поверхностью
Предложено много различных критериев прочности при сложно-напряженном состоянии изотропных тел [17]. В инженерных расчетах чаще других применяют критерий Шлейхера – Надаи
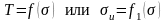 , (5.15)
, (5.15)
где вид функции в правой части устанавливается экспериментально по данным опытов для конкретных материалов.
В частности, при из (5.15) следует критерий Губера – Мизеса (5.14) или эквивалентный ему по форме энергетический критерий. Оба этих критерия основаны на гипотезе, по которой процесс разрушения зависит главным образом от изменения формы элемента тела.
При достижении потенциальной энергией формоизменения элемента тела предельного состояния наступает его разрушение или переход к пластической деформации.
Если
,
то из условия (5.15) следует обобщенный
критерии Мора
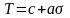 .
Используя формулы разд. 2, критерий
(5.15) можно сформулировать в терминах
максимального касательного
и нормального
напряжений:
.
Используя формулы разд. 2, критерий
(5.15) можно сформулировать в терминах
максимального касательного
и нормального
напряжений:
.
Например, относительно главных координатных осей при условии , обобщая соотношение (5.6), можно принять
.
4. При изучении анизотропии горных пород чаще всего ограничиваются изучением свойств горных пород в плоскости, параллельной напластованию, и плоскости, перпендикулярной к напластованию, считаю любое из направлений в этих плоскостях эквивалентным в отношении механических свойств. Такие тела принято называть трансверсально-изотропными.
 (5.16)
(5.16)
где - модули сдвига в плоскости и в перпендикулярных к ней плоскостях.
Для большинства горных пород модули сдвига рекомендуется вычислять по формулам
,
где - основной параметр анизотропии.
Известно, что прочность горных пород на сжатие существенно отличается от прочности на растяжение или сдвиг.
Сравнительно простым критерием прочности может служить, например, следующий [25]:
,
который представляет собой обобщение критерия Мора (5.6) относительно главных направлений.
Для хрупкого тела, подчиняющегося этому условию, должно выполняться следующее соотношение между пределами прочности на растяжение и сжатие в плоскости напластования и направлении , перпендикулярном к ней:
.
Постоянные А, В и С связаны с пределами прочности формулами вида
Предложены и более сложные критерии разрушения анизотропных тел [25], содержащие большое число констант, подлежащих определению на основании опытных данных. Однако использование их вряд ли возможно из-за больших трудностей в проведении опытов.
Из
(5.17) как частный случай следует критерий
прочности для изотропных тел
 :
:
, (5.17’)
где .
Этот критерий является одним из весьма полезных разновидностей общего критерия (5.15) для оценки прочности горных пород и цементного камня.
Опытами доказано, что деформация объема и величина предельного напряжения горной породы зависят исключительно от эффективных напряжений
,
где - коэффициент порового давления, характеризующий различную сопротивляемость скелета породы растяжению и сжатию; - модули объемной деформации расширения и сжатия соответственно. В это же время установлено, что изменение формы элемента тела не зависит от порового давления.
Следовательно, для учета поровых (пластовых) давлений необходимо во всех приведенных выше уравнениях состояния и критериях прочности нормальные напряжения и среднее давление заменить эффективными напряжениями и , оставив без изменения касательные напряжения .
Например, закон Гука (5.10) и критерий прочности (5.15) перепишутся в виде
; (5.10’’)
. (5.15’’)
В таком случае все исходные уравнения, включая и уравнения движения (1.45), будут содержать суммарные (тотальные) напряжения .
Для глин и глинистых пород, склонных к набуханию, компоненты деформации в уравнениях состояния (5.10’) необходимо дополнить слагаемыми , где - коэффициент объемного расширения при увлажнении породы; - начальная и текущая влажность породы.
Аналогично учитывается расширение (сжатие) любого твердого тела при нагревании (охлаждении) введением в уравнения состояния слагаемых , где - коэффициент объемного расширения при нагревании; ºС, ºС – начальная и текущая температура тела.
(4-3) КРИТЕРИИ РАЗРУШЕНИЯ НА ОСНОВЕ ТЕОРИИ ТРЕЩИН
Известно, что реальная прочность твердых тел во много раз меньше теоретической, равной , где Е – модель Юнга. Объясняется это тем, что реальные тела имеют разного рода микро- и макродефекты: трещины, поры, узкие полости, инородные включения и т.п. Распределение этих дефектов в объеме тела, как правило, случайно, и поэтому случайна величина прочности материала. Экспериментально это убедительно подтверждается тем, что наблюдается разброс (иногда довольно значительный) при испытаниях одинаковых образцов в одинаковых условиях, и имеет место так называемый масштабный эффект: большие образцы имеют меньшую прочность чем малые образцы той же формы. Это характерно для всех хрупких тел вообще, горных пород и тампонажного камня в частности.
Кроме того, современные экспериментальные данные свидетельствуют о постепенном развитии разрушения и о большой роли первичных дефектов в формировании картины разрушения. Трещины начинаются развивается задолго до полного разрушения тела. Разрушение не единовременный акт, оно развивается с большей или меньшей скоростью при сравнительно невысоких напряжениях и представляет собой некоторый динамический процесс (см. разд. 4.2).
Поэтому прежние представления о наступлении разрушения при достижении некоторого критического напряжения материала устарели.
Для оценки реальной прочности тел необходимо исходить из наличия в теле дефектов. При этом важное значение приобретает использование современных результатов теории трещин [33]. Хотя эти результаты не позволяют охватить все многообразие особенностей разрушения, но их использование дает инженеру необходимый инструмент для более правильной оценки прочности тел и для более глубокого понимания причин разрушения. С помощью теории трещин можно количественно объяснить больше различие между реальной и теоретической прочностью тел, влияние масштабного фактора, различие между прочностью на сжатие и растяжение и многое другое.
Гриффитс впервые показал, что низкая реальная прочность хрупких тел вызывается наличием трещин, приводящих к значительной концентрации напряжений. В основе теории Гриффитса лежит представление об энергетическом барьере – поверхностной энергии, который необходимо преодолеть для развития трещины, т.е. для образования новой поверхности. В то же время при увеличении трещины освобождается потенциальная энергия, которая может быть израсходована на разрушение.
Любой материал в данных условиях (температура, влажность, внешняя среда и т.д.) характеризуется некоторой плотностью поверхностной энергии , которая определяет величину работы, необходимую для образования единицы новой свободной поверхности. Энергетический критерий Гриффитса формулируется следующим образом: разрушение тела развивается, если плотность освобождающейся энергии достигает критического значения. Например, для трещины длиной 2l в поле равномерно растяжения напряжением p в условиях плоской деформации (рис. 52) критерий Гриффитса записывается в виде
,
где - потенциальная энергия тела.
Отсюда следует условие предельного равновесия при растяжении
. (4.33)
Если при данной длине трещины напряжение , то трещина не растет. Если же напряжение достигает критического значения , то трещина расширяется. Из формулы (4.33) вытекает, что не предельное напряжение - прочностная характеристика материала, а произведение
. (4.34)
В инженерных расчетах используется более удобный силовой критерий прочности Ирвина, который по существу эквивалентен критерию Гриффитса, но основан на особенности распределения напряжений в окрестности вершины трещины:
,
где r, - локальная система координат с началом в вершине трещины, k – коэффициент интенсивности напряжений (КИН), который зависит от формы тела, системы нагрузок и геометрии трещины.
Согласно критерию Ирвина, для каждого материала есть критическое значение коэффициента интенсивности напряжений , по достижении которого трещина начинает расти, т.е. для прочности тела необходимо, чтобы
.
Таким образом, для оценки влияния трещин на прочность тела необходимо решить соответствующую задачу теории упругости, найти КИН и сравнить его с опытной для данного материала величиной .
Напряжения и перемещения около вершины трещины для каждого типа раскрытия определяются коэффициентами интенсивности и нормального напряжения, поперечного и продольного сдвигов соответственно. Иногда в литературе используют другие обозначения КИН и вводят иные физические понятия. Например, согласно Г.И. Баренблатту, называют модулем сцепления, а - сдвиговым модулем сцепления.
В простейших случаях равномерного растяжения плоскости (рис. 52) плоского и антиплоского сдвигов (рис. 54) коэффициенты интенсивности напряжений вычисляются по формулам
,
где - соответственно силы растяжения, плоского и антиплоского сдвигов.
, (4.35)
где - угол начального распространения трещины относительно ее направления (ориентации).
Отсюда и находятся критические значения внешней нагрузки, при которой начинается локальное разрушение тела. Например, при равномерном растяжении или сжатии плоскости с трещиной, расположенной под углом к направлению внешней силы, имеют место следующие формулы для определения:
Коэффициентов интенсивности напряжений
;
угла начального распространения трещины
.
Предельного напряжения
,
где верхние знаки соответствуют растяжению, а нижние – сжатию; -критическое значение напряжения при растяжении плоскости с трещиной, перпендикулярной к направлению растяжения [см. рис. 52 и формулу (4.33)].
Коэффициенты интенсивности напряжений при указанных на рис. 57 видах нагружения вычисляются по формуле [7]
,
где
разрушение образца в целом определяется локальной прочностью его наиболее слабого элемента объема.
Функция распределения прочности при хрупком разрушении представляется следующим образом:
(4.36)
где - параметры закона распределения, подлежащие определению из опытов.
Последнее выражение с помощью двукратного логарифмирования можно преобразить в уравнение прямой
в координатах и . Обычно для построения прямой используются абсциссы и соответствующие им ординаты , где ; т – номер наблюдаемого значения прочности (расположены в порядке возрастания); п – общее число наблюдений.
Для определения параметров и используется либо графическое построение, либо метод наименьших квадратов. В результате
,
где - значение х при у = 0.
Доказано, что параметр связан с объемом тела. Если найден параметр для образца объемом , то для образца объемом будет .
Вероятность разрушения образца под действием напряжения вычисляется по формуле
,
где отношение можно рассматривать как коэффициент безопасности.
Отсюда легко доказать, что для двух образцов, объемы которых и , разрушение равновероятно, если выполняется соотношение
.
В общем случае результаты испытаний на прочность могут быть приближены одним уравнением (4.36) лишь в довольно ограниченном интервале. Чаще для адекватного описания требуются две прямые с различным наклоном. Точка пересечения этих прямых может означать изменение самого механизма разрушения.
Для того, чтобы определить влияние на хрупкое разрушение неоднородного поля напряжений, сравнивают наибольшее напряжение в неоднородном поле напряжений в момент разрушения с разрушающим напряжением в однородном поле, используя условие равной вероятности разрушения.
Например, в случае чистого изгиба балки имеет место следующее соотношение между прочностью на изгиб и прочностью на растяжение:
,
где V – объем образца, испытываемого на растяжение; - объем балки. Если, например, и , то .
Статистический подход к хрупкому разрушению при трехмерном напряженном состоянии может быть основан на допущении, что по отношению к разрушению напряжения не взаимодействуют. Тогда сравнение с вероятностью разрушения под действием одноосного нагружения напряжением дает уравнение равной вероятности разрушения
,
представляющее собой условие трехмерного разрушения.
(4-4) ОБЩАЯ СИСТЕМА УРАВНЕНИЙ МЕХАНИКИ ДЕФОРМИРУЕМОГО ТВЕРДОГО ТЕЛА
получить аналитическое решение задачи механики деформируемого твердого тела – значит определить прежде всего компоненты вектора перемещения , тензоров деформаций и напряжения в любой точке области D, занятой телом, и в любой момент времени.
В общем случае, как показано ранее, 15 искомых функций должны удовлетворять следующим 15 уравнениям.
Трем уравнениям движения [см. формулу (1.45)]
. (4.37)
Шести уравнениям механического состояния
(4.38)
соответственно при упругой деформации изотропного тела [см. формулу (4.9)]; при упругопластической деформации изотропного тела [см. формулу (4.12)]; при ползучести среды [см. формулу (4.26)]. Возможны уравнения другого вида, связывающие компоненты и , в зависимости от рассматриваемого состояния тела и действующих факторов (см. разд. 4.2).
Шести уравнениям совместимости (неразрывности) деформаций Сен-Венана [см. формулу (1.24)]
(4.39)
и т.д. (остальные уравнения получаются круговой заменой индексов) при рассмотрении кратковременного напряженно-деформированного состояния тела. При изучении ползучести тела используются шесть аналогичных уравнений совместимости скоростей деформаций .
В
уравнениях (4.37) – (4.39) использована
декартова система координат
и следующие введенные ранее обозначения:
- проекции массовых сил и ускорения;
-
плотность тела;
- модуль сдвига;
- коэффициент Ламе;
- модуль объемного сжатия; Е,
v
– модуль Юнга и коэффициент Пуассона;
и
 - модули пластичности и ползучести,
являющиеся соответственно функциями
интенсивности деформации сдвига Г и
интенсивности скорости деформации
сдвига Н (см. раздел 1.3);
- компоненты девиатора деформации;
- объемная деформация;
- компоненты девиатора скорости
деформации;
- символ Кронекера:
- модули пластичности и ползучести,
являющиеся соответственно функциями
интенсивности деформации сдвига Г и
интенсивности скорости деформации
сдвига Н (см. раздел 1.3);
- компоненты девиатора деформации;
- объемная деформация;
- компоненты девиатора скорости
деформации;
- символ Кронекера:

где - скорость объемной деформации; и - компоненты тензоров деформаций и скоростей деформаций; связанные соответственно с компонентами перемещения и скорости соотношениями Коши:
(4.40)
При переходе к криволинейной системе координат вид всех уравнений, кроме уравнений (4.38), изменится. В разд. 1.3 и 1.4 приведены формулы перехода к цилиндрической системе координат.
Для однозначного определения напряженно-деформированного состояния тела к уравнениям (4.37) – (4.39) необходимо присоединить начальное и граничные условия. Различают три основные граничные задачи механики деформируемого твердого тела.
Если на поверхности S, ограничивающей область D тела, задан вектор напряжения , то граничные условия записываются в виде (см. разд. 1.4)
(4.41)
где - нормаль к поверхности S; - проекции вектора на оси выбранной системы координат; М – точка поверхности; t – время.
В этом случае говорят о первой основной граничной задаче.
Если на поверхности S заданы условия для компонент вектора перемещения (или скорости )
(4.42)
то говорят о второй граничной задаче, где - известные функции точек поверхности и времени.
В том случае, когда на одной части поверхности S задано условие вида (4.41), а на другой – вида (4.42), говорят о третьей основной граничной задаче, иногда ее называют смешанной граничной задачей.
Отличительная особенность первой основной граничной задачи состоит в том, что ее решение в зависимости от удобства можно строить в перемещениях (скоростях) или в напряжениях. Вторую и третью граничные задачи можно решать только в перемещениях (скоростях).
Решить задачу в перемещениях – значит представить исходную систему уравнений, граничные и начальные условия через функции . Для этого достаточно подставить формулы (4.38) и (4.40) в уравнения (4.37) и граничные условия (4.41). полученная таким образом система трех уравнений и трех граничных условий будет содержать только перемещения . В этом случае надобность в уравнениях (4.39) отпадает. Они могут служить лишь для контроля полученного решения.
Если первая граничная задача решается в напряжениях , то эти функции, кроме уравнений (4.37), должны удовлетворять и системе уравнений (4.39), в которой необходимо (или ) выразить через с помощью формул (4.38).
Ясно, что вид и характер исходной системы уравнений зависит от вида соотношений (4.38). С различными частными системами таких уравнений можно познакомиться по справочной литературе, учебникам и монографиям. При решении конкретных задач мы будем получать эти уравнения в упрощенном виде.
Определение напряженно-деформированного состояния тела не может быть самоцелью. Оно лишь предпосылка для оценки прочности, устойчивости, долговечности тела, конструкции или сооружения.
4.5 §3. ОПРЕДЕЛЕНИЕ ВЗАИМОДЕЙСТВИЙ СРЕД «ПОРОДА-КРЕПЬ»
Осложнения, связанные с разрушением горных пород в процессе бурения скважины на первоначальном этапе предупреждают подбором свойств бурового раствора, а затем создается крепь скважины из обсадных колонн и цементных оболочек, основная функция которых – изоляция и разобщение пластов.
Величина внешнего воздействия на крепь не всегда известна, однако вопросы прочности и долговечности необходимо решать в период строительства скважины.
Рассмотрим напряженно-деформированное состояние системы горная порода – крепь, где основное значение имеет давление рк на поверхности контакта горной породы и цементной оболочки, отсутствующее на начальной стадии строительства скважины, а затем появляющееся и развивающееся как функция времени.
Возникновение и развитие давления на крепь скважины рк возможно при ползучести и текучести люлинворских глин вследствие их начального напряженного состояния.
Давление рк зависит от времени, жесткости С крепи скважины и от реологических свойств горных пород.
Рассмотрим модель вязкопластичной изотропной горной породы, решать которую будем при следующих допущениях:
1.
Начальное напряженное состояние
определяем гравитационной силой
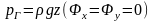 ,
поровым давлением рп(z)
и условием нулевого смещения в
горизонтальной плоскости
,
поровым давлением рп(z)
и условием нулевого смещения в
горизонтальной плоскости
 т.е. следующими эффективными напряжениями
т.е. следующими эффективными напряжениями
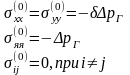 (4.5)
(4.5)
где
 -
средняя плотность вышележащих горных
пород, z
– глубина расчетного участка,
-
средняя плотность вышележащих горных
пород, z
– глубина расчетного участка,
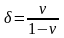 -
коэффициент бокового горного давления;
-
коэффициент бокового горного давления;
2. Горная порода – это однородное изотропное упругое, упругопластичное или вязкопластичное твердое тело типа глин и солей;
3. Скважина – это круглая вертикальная цилиндрическая полость в корном массиве, заполненная буровым раствором пластичностью с;
4. Силы инерции аi очень малы, т.е. горные породы находятся в стационарном состоянии.
В
результате приведенных допущений
напряженно-деформированное состояние
приствольной зоны скважины характеризуется
осевой симметрией и равенством нулю
напряжений и деформаций сдвига ( ).
).
Нормальные напряжения и перемещения представим для цилиндрической системы координат:
 (4.6)
(4.6)
где
 -
дополнительное эффективное напряжение
и
-
дополнительное эффективное напряжение
и
 -
дополнительное радиальное перемещение.
-
дополнительное радиальное перемещение.
В
формуле (4.6) принято, что дополнительное
осевое перемещение
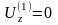 ,
т.е.
,
т.е.
 .
(4.7)
.
(4.7)
Поэтому
относительно дополнительных величин
 ,
,
 и
и
 ,
,
 (4.8)
(4.8)
имеем задачу о плоской деформации.
Напряжения должны удовлетворять следующим условиям равновесия см. формулу (2.9)
 (4.9)
(4.9)
Согласно условию 3 и формулам (4.5)-(4.7) – граничным условиям
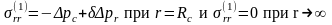 (4.10)
(4.10)
где
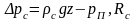 -
радиус скважины.
-
радиус скважины.
Выбор механического уравнения состояния (3.94) зависит от основной деформационной характеристики данной горной породы:

Если деформация ползучести породы мала (не выше 10% от мгновенной) и диаграмма кратковременного нагружения σ1 ~ ε1, имеет вид кривых 1, 2, 3, 5 или 4, 6 (см. рис 14) то выбирается модель упругого или упруго-пластичного тела. При деформации ползучести значительно превосходящей мгновенную (упругую или пластичную) деформацию, выбирается модель вязкого тела.
Приводим решения задач о напряженно-деформированном состоянии приствольной зоны скважины, принимая для указанных трех типов деформирования простейшие модели. Кроме того, дана оценка устойчивости стенки скважины и определено допустимое давление в стволе скважины, используя различные критерии прочности горных пород.
1.
Для упругой модели горной породы
уравнения, связывающие искомые величины
 и
и
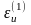 имеют
вид [см. формулы (3.94)]
имеют
вид [см. формулы (3.94)]
 ,
,
или, согласно условию (4.7) и соотношениям (4.8)
 ,
,
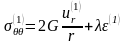 ,
(4.11)
,
(4.11)
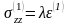 ,
,
где
 дополнительная величина объемной
деформации;
дополнительная величина объемной
деформации;
G = E/2(1+v) и λ = 2vG/(1-2V)—упругие константы Ламе.
Так
как все напряжения
выражаются через одну функцию
 ,
то решать задачу целесообразно в
перемещении.
,
то решать задачу целесообразно в
перемещении.
Подстановка (4.11) в (4.9) дает
 .
.
Поэтому
 .
.
Интегрируя, найдем общее решение

и следовательно, по формулам (4.11) – напряжения
 ,
,
 ,
,
 .
.
Из граничных условий (4.10) следует
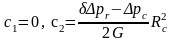 .
.
Поэтому
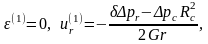
 ,
,
 ,
,
 .
.
После подстановки этих формул в (4.6) получим окончательно
 ,
,
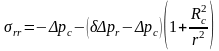 ,
(4.12)
,
(4.12)

Видно, что напряжения σθθ принимает максимальное значение у стенки скважины (r = Rc). Здесь же максимальна и интенсивность напряжений
 ,
(4.13)
,
(4.13)
где
 -
приведенное давление в скважине. Величина
среднего давления
-
приведенное давление в скважине. Величина
среднего давления
 .
(4.14)
.
(4.14)
Легко
заметить, что образование скважины
приводит к изменению интенсивности
напряжений горных пород, среднее давление
при этом остается без изменения. Из
решения (4.13) следует, что напряженное
состояние породы у стенки скважины
будет отличаться от напряженного
состояния нетронутого массива только
при q
 δ. При q
= δ
величина
δ. При q
= δ
величина
 минимальна. Это означает, что при давлении
в скважине
минимальна. Это означает, что при давлении
в скважине
 обеспечиваются наилучшее условие для
сохранения устойчивости стенки скважины.
Но исходить из такого требования при
выборе, например, плотности бурового
раствора не рационально, так как оно
может привести к неоправданному
перерасходу материалов.
обеспечиваются наилучшее условие для
сохранения устойчивости стенки скважины.
Но исходить из такого требования при
выборе, например, плотности бурового
раствора не рационально, так как оно
может привести к неоправданному
перерасходу материалов.
Для кратковременной устойчивости стенки скважины воспользуемся критерием прочности (2.82). Подстановка формул (4.13) и (4.14) в этот критерий дает следующее необходимое условие устойчивости и прочности пород при r= Rc:
 ,
(4.15)
,
(4.15)
где
 .
.
Нарушение левостороннего ограничения может привести к мгновенному осыпанию породы, а правостороннего — к гидроразрыву пласта. Поэтому величина q = qmin (или, иначе, давление в скважине pc=pп+qminΔpr) является минимально допустимой, а величина q = qmax или рс=Рп + qmaxΔpr — максимально допустимой.
Формулу
для расчета σ*,
можно упростить, если принять во внимание,
что для большинства пород α
= 8 —10 и
 .
Поэтому, приняв α = 9 и
.
Поэтому, приняв α = 9 и
 ,
получим с некоторым запасом прочности
,
получим с некоторым запасом прочности
 (4.16)
(4.16)
Допустимый диапазон изменения параметра q приведен ниже.
q |
0,25 |
0,33 |
0,43 |
0,52 |
0,66 |
0,81 |
1 |
qmin. |
-0,43 |
-0,46 |
-0,47 |
-0,5 |
-0,51 |
-0,51 |
-0,5 |
qmax |
0,93 |
1,12 |
1,35 |
1,54 |
1,83 |
2,15 |
2,5 |
Видно, что нижняя граница qmin практически не зависит от коэффициента бокового горного давления и кратковременная устойчивость стенки скважины возможна при q = - 0,5 или рс= рп – 0,5рr.
Если, например, глубина скважины Н = 3000 м, средняя плотность пород рг = 2300 кг/м3, коэффициент аномальности порового давления kа = 1,5, т.е. рr = 69 МПа и рп = 45 МПа, то получим pс = 33 МПа. Следовательно, при промывке скважины плотность бурового раствора не должна быть ниже рс = 1100 кг/м3.
Рост параметра qmax с увеличением коэффициента δ объясняется увеличением коэффициента Пуассона ν, т. е. более плотной упаковкой пород.
Для
нормально и сильноуплотненных пород
диапазон допустимого давления в
скважине достаточно широк. Но этот
диапазон сужается с увеличением
коэффициента аномальности. Например,
при δ
= 0,25 (ν
= 0,2) Кa=рп/рг.с
= 2 и рr/рrс
= 2,3, используя значения qmin
= -0,43 и qmax=
0,93, получим 1,87 рс/pr.с
2,28,
где pr.с
— гидростатическое давление.
рс/pr.с
2,28,
где pr.с
— гидростатическое давление.
Этим объясняется сложность согласованного выбора плотности бурового раствора и режима промывки при бурении пород с аномально высоким поровым давлением. В таких условиях первостепенное значение приобретает точный выбор плотности и реологии бурового раствора, компоновки инструмента и диаметра долота, режима промывки и СПО, обеспечивающих изменение давления рс в пределах допустимого диапазона. Подчеркнем, что допустимый диапазон изменения давления в скважине (4.53) является лишь необходимым, но не достаточным, так как не учитывает время воздействия бурового раствора.
Для обеспечения устойчивости стенок скважины в течение заданного периода времени Т воспользуемся критерием длительной прочности. Учитывая интенсивность напряжений (4.51) и начальное условие (4.53), получим
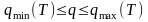 (4.17)
(4.17)
где
 .
.
Ниже показан характер сужения допустимого интервала во времени при δ = 0,5 и n = 2.
Т/t0 |
0 |
0,2 |
0,6 |
1 |
1,4 |
2 |
3 |
5 |
10 |
qmin |
-0,5 |
-0,29 |
-0,1 |
0 |
0,06 |
0,12 |
0,18 |
0,24 |
0,32 |
qmax |
1,5 |
1,29 |
1,1 |
1 |
0,94 |
0,88 |
0,82 |
0,76 |
0,68 |

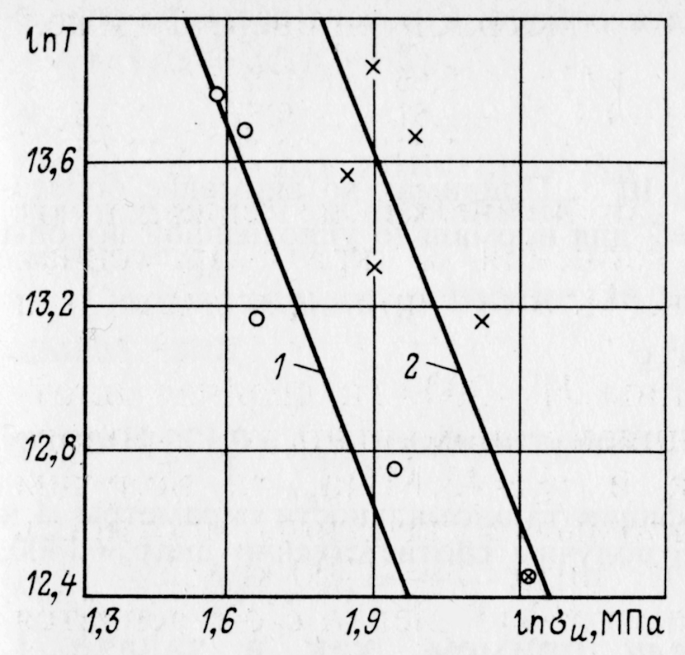
Рис. 36. Диаграммы устойчивости глин Рис. 37. Диаграммы устойчивости
разной плотности по данным бурения нормально уплотненных пород скважин с использованием бурового по данным бурения скважин с
раствора, обработанного УЩР использованием двух типов
бурового раствора при обработке
УЩР в отложениях эоцена;
КСl в меловых отложениях
Видно, что рост периода времени Т сопровождается увеличением qmin и уменьшением qmax. Вначале это происходит достаточно интенсивно, а затем интенсивность значительно падает. При Т/t0>>1 влияние параметра σ*, пренебрежимо мало. Характерно, что после определенного значения Т/t0 минимально допустимая величина q 0, т. е. рс рп Применимость критерия устойчивости (4.17) была проверена по данным бурения Левкинской и Юбилейной площадей ПО «Краснодарнефтегаз».
На рис. 36 и 37 приведены диаграммы длительной устойчивости различных пород, которые позволили определить значения параметров долговечности. Для геологического разреза Левкинской площади получено: n = 3,5, A = 8,9 10-10 при плотности глин pr = 2.0 – 2.04 103 кг/м3 и А = 3,3 10-10 при pr = 2.1 – 2.18-103 кг/м3, где напряжения принимали в МПа, время — в с. Для разреза Юбилейной площади получено: n = 2, A = 10-9 при использовании глинистого раствора, обработанного УЩР, и А = 4,5-10-10—для раствора, обработанного КС1. Приведем пример использования полученных моделей.
Пусть требуется найти минимально допустимую плотность ингибированного бурового раствора для вскрытия меловых отложений в интервале 3200—4000 м, если средняя плотность вышележащих пород р = 2500 кг/м3, δ= 0,5 и технологически необходимое время от вскрытия до крепления интервала составляет Т= 6,4*105с
Согласно (4.17) минимально допустимая плотность бурового раствора определяется по формуле
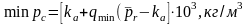
где
kа—
коэффициент аномальности,
 Принимая
во внимание определенные выше
параметры А = 4,5 10-10
и n
= 2 для нормально уплотненной породы ka
= 1, найдем
Принимая
во внимание определенные выше
параметры А = 4,5 10-10
и n
= 2 для нормально уплотненной породы ka
= 1, найдем

и, так как Т/t0 = 2, по вышеприведенной таблице находим qmin = 0,12 Поэтому
min pc=1180 кг/м3
Если предположить, что с ростом коэффициента аномальности параметры А и n не изменяются, то при ka=1,2, 1,4 и 1,6 получим соответственно
min pс=1400, 1600 и 1800 кг/м3
2. Для упругопластичной модели примем как в задаче 1, справедливыми соотношения
 (4.18)
(4.18)
где
с
– постоянная, подлежащая определению.
Тогда компоненты деформаций
 будут
будут



а интенсивность деформаций сдвига [см. формулу (1.21)]

Согласно деформационной теории пластичности уравнения состояния () в этом случае принимают вид


где
 - новая переменная; g(x)
определяется по деформационной кривой
- новая переменная; g(x)
определяется по деформационной кривой
…….
3. Для вязкопластичной модели горной породы решение задачи не будет принципиально отличаться от упругопластичной, если исходить из теории старения или установившейся ползучести…….
