
- •Кинематика сплошной среды
- •Элементы теории деформаций
- •Динамические величины и элементы теории напряжений
- •Раздел 2. (4) Уравнения механики сплошных сред
- •§ 1. Уравнение неразрывности
- •§ 2. Уравнения движения и равновесия
- •§ 3. Уравнения состояния (математические модели)
- •§ 1. Уравнение неразрывности
- •§ 2. Уравнения движения и равновесия
- •Уравнением моментов
- •§ 3. Уравнения состояния (математические модели)
- •§ 4. Уравнения состояния гидромеханики
- •§ 5. Основные уравнения теории фильтрации
- •§ 5.1 Линейные уравнения и граничные задачи фильтрации.
- •§ 6. Мгновенные уравнения состояния и критерии прочности
- •§ 7. Временные уравнения состояния и критерии длительной прочности
- •§ 8. Общая система уравнений механики деформируемого твердого тела
- •Задачи гидромеханики в бурении
- •§ 1. Базовые задачи гидродинамики при промывке и цементировании скважин
- •§ 2. Ламинарное и турбулентное течение жидкостей в щелевом канале
- •§ 3. Ламинарное и турбулентное течение жидкостей в кольцевом канале
- •§ 4. Задачи фильтрации при строительстве скважин
- •Формула дюпюи и ее обобщения
- •§1. Среды в механике сплошной среды
- •§2. Горные породы
- •§ 3. Критерии разрушения сред на основе теории трещин
- •§ 4. Порода - деформируемое твердое тело
- •§ 5. Реологические свойства
- •§ 6. Задачи устойчивости горных пород в скважинах
- •Напряженное состояние и устойчивость анизотропных пород в вертикальных и наклонных скважинах
- •4.10. Определение горного давления на крепь ствола скважины
- •4.11. Центрирование бурильных и обсадных колонн.
§ 8. Общая система уравнений механики деформируемого твердого тела
Получить
аналитическое решение задачи механики
деформируемого твердого тела – значит
определить прежде всего компоненты
вектора перемещения
 ,
тензоров деформаций
и напряжения
,
тензоров деформаций
и напряжения
 в
любой точке области D,
занятой телом, и в любой момент времени.
в
любой точке области D,
занятой телом, и в любой момент времени.
В общем случае, как показано ранее, 15 искомых функций должны удовлетворять следующим 15 уравнениям.
Трем уравнениям движения [см. формулу (2.9)]
 .
(2.98)
.
(2.98)
Шести уравнениям механического состояния
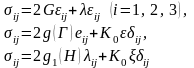 (2.99)
(2.99)
соответственно при упругой деформации изотропного тела [см. формулу (2.74)]; при упругопластической деформации изотропного тела [см. формулу (2.77)]; при ползучести среды [см. формулу (2.91)]. Возможны уравнения другого вида, связывающие компоненты и , в зависимости от рассматриваемого состояния тела и действующих факторов.
Шести уравнениям совместимости (неразрывности) деформаций Сен-Венана [см. формулу (1.24)]
 (2.100)
(2.100)
и т.д. (остальные уравнения получаются круговой заменой индексов) при рассмотрении кратковременного напряженно-деформированного состояния тела. При изучении ползучести тела используются шесть аналогичных уравнений совместимости скоростей деформаций .
В
уравнениях (2.98) – (2.100) использована
декартова система координат
 и следующие введенные ранее обозначения:
и следующие введенные ранее обозначения:
 - проекции массовых сил и ускорения;
-
плотность тела;
- проекции массовых сил и ускорения;
-
плотность тела;
 - модуль сдвига;
- модуль сдвига;
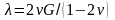 - коэффициент Ламе;
- модуль объемного сжатия; Е,
v
– модуль Юнга и коэффициент Пуассона;
и
- коэффициент Ламе;
- модуль объемного сжатия; Е,
v
– модуль Юнга и коэффициент Пуассона;
и
 - модули пластичности и ползучести,
являющиеся соответственно функциями
интенсивности деформации сдвига Г и
интенсивности скорости деформации
сдвига Н (см. лекцию 1);
- модули пластичности и ползучести,
являющиеся соответственно функциями
интенсивности деформации сдвига Г и
интенсивности скорости деформации
сдвига Н (см. лекцию 1);
 - компоненты девиатора деформации;
- компоненты девиатора деформации;
 - объемная деформация;
- объемная деформация;
 - компоненты девиатора скорости
деформации;
- компоненты девиатора скорости
деформации;
 - символ Кронекера:
- символ Кронекера:

где
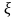 - скорость объемной деформации;
и
- компоненты тензоров деформаций и
скоростей деформаций; связанные
соответственно с компонентами перемещения
и скорости
- скорость объемной деформации;
и
- компоненты тензоров деформаций и
скоростей деформаций; связанные
соответственно с компонентами перемещения
и скорости
 соотношениями Коши:
соотношениями Коши:
 (2.101)
(2.101)
При переходе к криволинейной системе координат вид всех уравнений, кроме уравнений (2.99), изменится. В лекции 1 приведены формулы перехода к цилиндрической системе координат.
Для однозначного определения напряженно-деформированного состояния тела к уравнениям (2.98) – (2.100) необходимо присоединить начальное и граничные условия. Различают три основные граничные задачи механики деформируемого твердого тела.
Если
на поверхности S,
ограничивающей область D
тела, задан вектор напряжения
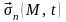 ,
то граничные условия записываются в
виде (см. лекцию 1)
,
то граничные условия записываются в
виде (см. лекцию 1)
 (2.102)
(2.102)
где
- нормаль к поверхности S;
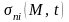 - проекции вектора
на оси выбранной системы координат; М
– точка поверхности; t
– время.
- проекции вектора
на оси выбранной системы координат; М
– точка поверхности; t
– время.
В этом случае говорят о первой основной граничной задаче.
Если
на поверхности S
заданы условия для компонент вектора
перемещения
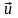 (или
скорости
)
(или
скорости
)
 (2.103)
(2.103)
то
говорят о второй
граничной задаче,
где
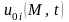 - известные функции точек поверхности
и времени.
- известные функции точек поверхности
и времени.
В том случае, когда на одной части поверхности S задано условие вида (2.102), а на другой – вида (2.103), говорят о третьей основной граничной задаче, иногда ее называют смешанной граничной задачей.
Отличительная особенность первой основной граничной задачи состоит в том, что ее решение в зависимости от удобства можно строить в перемещениях (скоростях) или в напряжениях. Вторую и третью граничные задачи можно решать только в перемещениях (скоростях).
Решить
задачу в перемещениях – значит представить
исходную систему уравнений, граничные
и начальные условия через функции
 .
Для этого достаточно подставить формулы
(2.99) и (2.101) в уравнения (2.98) и граничные
условия (2.102), полученная таким образом
система трех уравнений и трех граничных
условий будет содержать только перемещения
.
В этом случае надобность в уравнениях
(2.100) отпадает. Они могут служить лишь
для контроля полученного решения.
.
Для этого достаточно подставить формулы
(2.99) и (2.101) в уравнения (2.98) и граничные
условия (2.102), полученная таким образом
система трех уравнений и трех граничных
условий будет содержать только перемещения
.
В этом случае надобность в уравнениях
(2.100) отпадает. Они могут служить лишь
для контроля полученного решения.
Если
первая граничная задача решается в
напряжениях
 ,
то эти функции, кроме уравнений (2.98),
должны удовлетворять и системе уравнений
(2.100), в которой необходимо
(или
)
выразить через
с помощью формул (2.99).
,
то эти функции, кроме уравнений (2.98),
должны удовлетворять и системе уравнений
(2.100), в которой необходимо
(или
)
выразить через
с помощью формул (2.99).
Ясно, что вид и характер исходной системы уравнений зависит от вида соотношений (2.99). С различными частными системами таких уравнений можно познакомиться по справочной литературе, учебникам и монографиям. При решении конкретных задач мы будем получать эти уравнения в упрощенном виде.
Определение напряженно-деформированного состояния тела не может быть самоцелью. Оно лишь предпосылка для оценки прочности, устойчивости, долговечности тела, конструкции или сооружения.
Лекция 3. Основные задачи механики сплошных сред в бурении
