Задача 5

Дані про роздрібний товарообіг і доходи населення в умовних грошових одиницях в деякій країні за 1996-2007рр. представлені в табл.5.1.

Таблиця 5.1 – Роздрібний товарообіг і доходи населення

Рік	Роздрібний товарообіг, млн. умов. од.,	Доходи населення, млн. умов. од., X
1996	236	257
1997	254	275
1998	267	293
1999	281	309
2000	290	319
2001	311	337
2002	325	350
2003	335	364
2004	355	385
2005	375	405
2006	401	437
2007	431	469

Необхідно розрахувати методом найменших квадратів оцінки параметрів споживчої функції; перевірити достовірність вибраної лінії регресії методом аналізу дисперсій; оцінити лінійний коефіцієнт кореляції; визначити довірчі інтервали для та ; побудувати на одному графіку вихідні дані та знайдену лінію регресії.

Розв’язання

5.1 Оцінка параметрів споживчої функції

Зв’язок між роздрібним товарообігом і доходом населення носить прямолінійний характер, тому споживча функція має вигляд [3]:

, (5.0)

де – роздрібний товарообіг;

– особисті доходи громадян;

– константа;

– кутовий коефіцієнт кореляції;

– стохастична складова (залишки).

Для оцінювання параметрів та в рівнянні (5.1) скористаємось методом найменших квадратів (МНК). Запишемо систему нормальних рівнянь [3]:

(5.0)

. (5.0)

Для знаходження та запишемо рівняння оцінок:

, (5.0)

, (5.0)

де – моменти першого порядку;

– моменти другого порядку.

; (5.0)

; (5.0)

; (5.0)

; (5.0)

. (5.0)

Для зручності розрахунку моментів побудуємо таблицю 5.2.

Таблиця 5.2 – Проміжні розрахунки

Рік
1996	236	55696	257	66049	60652	-93	8649
1997	254	64516	275	75625	69850	-75	5625
1998	267	71289	293	85849	78231	-57	3249
1999	281	78961	309	95481	86829	-41	1681
2000	290	84100	319	101761	92510	-31	961
2001	311	96721	337	113569	104807	-13	169
2002	325	105625	350	122500	113750	0	0
2003	335	112225	364	132496	121940	14	196
2004	355	126025	385	148225	136675	35	1225
2005	375	140625	405	164025	151875	55	3025
2006	401	160801	437	190969	175237	87	7569
2007	431	185761	469	219961	202139	119	14161
Всього	3861	1282345	4200	1516510	1394495		46510

; (5.0)

; (5.0)

; (5.0)

; (5.0)

; (5.0)

; (5.0)

. (5.0)

Таким чином, маємо споживчу функцію:

. (5.0)

5.2 Перевірка достовірності підібраної лінії регресії методом аналізу дисперсій за критерієм Фішера

Розрахуємо критерій Фішера [3]:

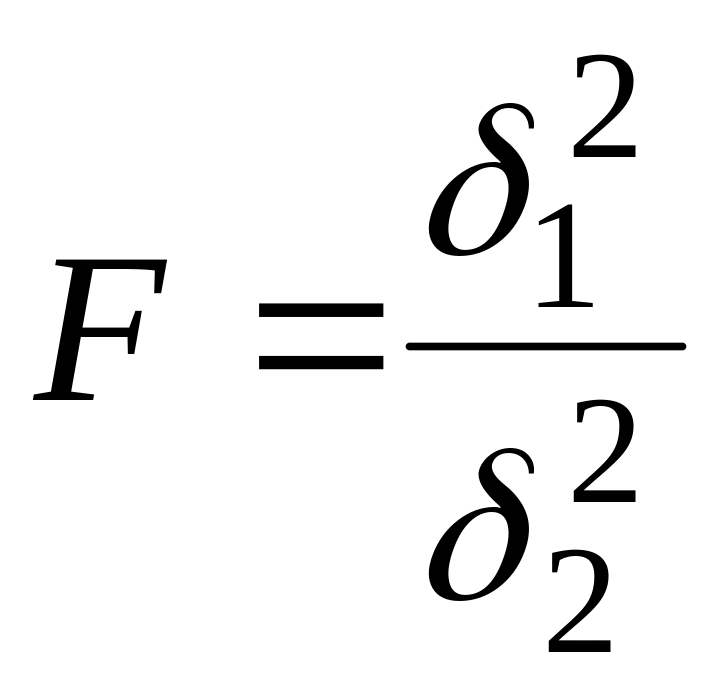(5.0)

де – обґрунтована складова дисперсії;

– необґрунтована складова дисперсії;

– загальна дисперсія;

, (5.0)

де – емпіричне значення ;

– теоретичне значення ;

– середнє значення ;

, (5.0)

. (5.0)

Виходячи з даних міркувань:

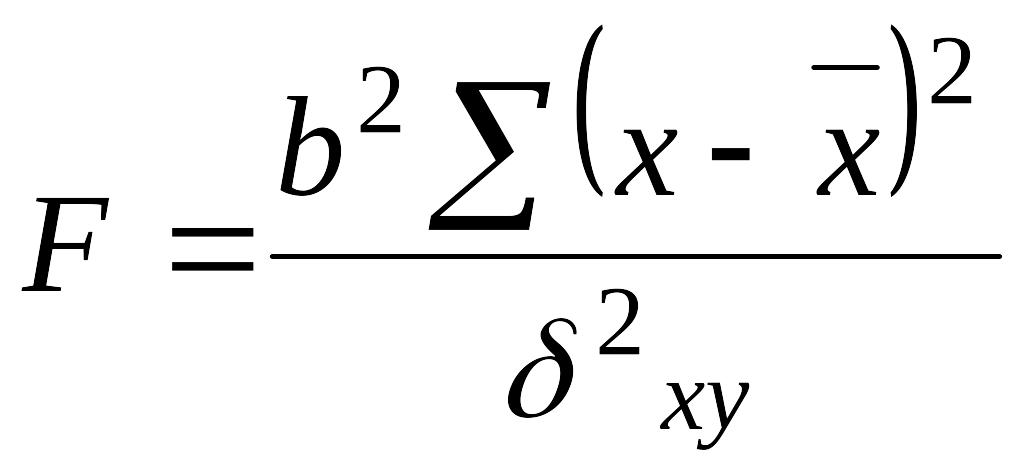(5.0)

Таблиця 5.3 – Таблиця аналізу дисперсій

Компоненти дисперсії	Число ступенів свободи,	Сума квадратів,	Середнє значення суми квадратів,
Регресія	1
Відхилення від регресії
Всього

Таблиця 5.4 – Таблиця аналізу дисперсій стосовно даних задачі

Компоненти дисперсії	Число ступенів свободи,	Сума квадратів,	Середнє значення суми квадратів,
Регресія	1	(0,928)2*46510=40021,86	40021,86
Відхилення від регресії	10	10*4,48=44,8	4,48
Всього	11	40066,66

, (5.0)

. (5.0)

Таким чином:

, (5.0)

де – число ступенів свободи відповідно чисельника і знаменника.

. (5.0)

, , тобто розходження обґрунтованої та необґрунтованої складових дисперсії носить не випадковий характер і взаємозв’язок між рівнем споживання та рівнем доходу тісний.

5.3. Оцінка лінійного коефіцієнту кореляції

Оцінку лінійного коефіцієнта кореляції r виконаємо за такою формулою [3]:

, (5.0)

. (5.0)

Високий лінійний коефіцієнт кореляції свідчить про тісний взаємозв’язок між роздрібним товарообігом та рівнем доходу.

5.4 Побудова довірчих інтервалів для , та .

Побудова довірчого інтервалу  для кутового коефіцієнту кореляції виконаємо за такою формулою [3]:

, (5.0)

де – деяка похибка при оцінці ;

– довірчий коефіцієнт при рівні імовірності та ступенях свободи. Знаходиться за таблицями –розподілу Ст’юдента.

Приймається якісна гіпотеза, відповідно до якої .

Формула для розрахунку має вигляд [3]:

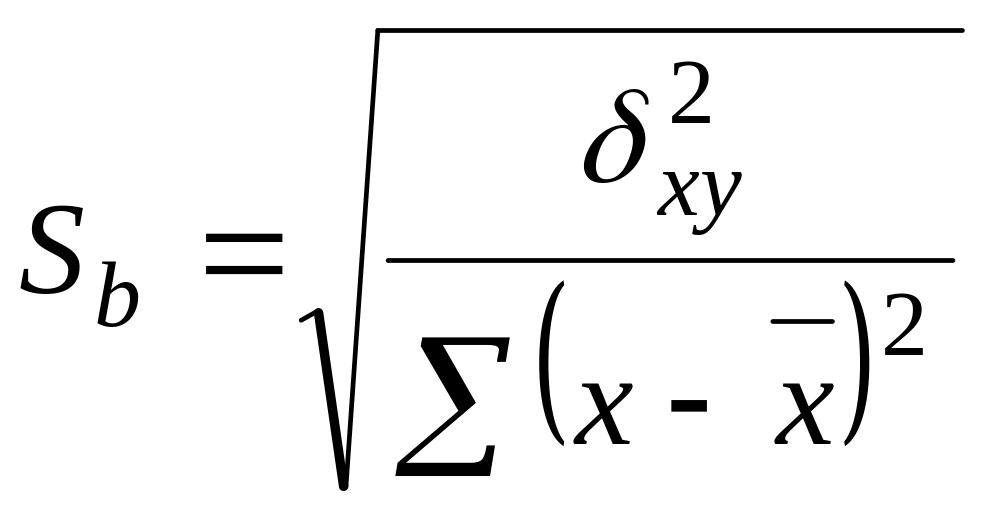, (5.0)

. (5.0)

; (5.0)

; ; (5.0)

. (5.0)

Знайдений інтервал не має значень 0 та 1, тому результати регресії відповідають якісній гіпотезі, згідно до якої , тому робимо висновок про достатню точність оцінки .

Побудову довірчого інтервалу для коефіцієнта виконаємо за такою формулою [3]:

, (5.0)

де – деяка похибка при оцінюванні ;

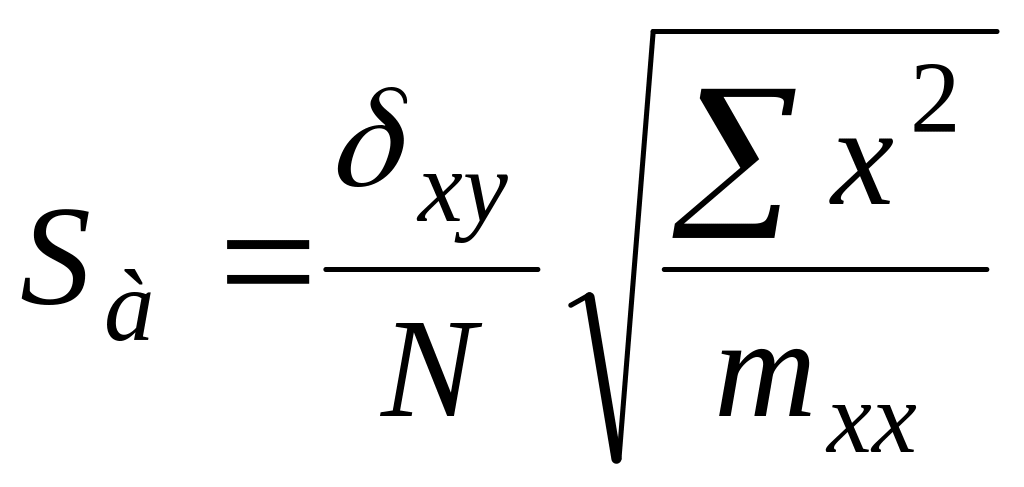, (5.0)

. (5.0)

; ; (5.0)

(5.0)

До інтервалу входять як від’ємні, так і додатні значення, отже при 95% імовірності похибка при оцінюванні не істотно відмінна від нуля.

Побудову довірчого інтервалу для лінійного коефіцієнту кореляції виконаємо за такою формулою [3]:

, (5.0)

де – деяка похибка при оцінці ;

– деяка функція при рівні імовірності , коефіцієнті кореляції та деякій точковій оцінці . Оскільки не можна визначити, а, значить, і значення всієї функції невідоме, необхідно скористатися -перетворенням Фішера. Для цього вводимо нову змінну :

(5.0)

Розподіл приблизно співпадає з нормальним розподілом.

Тоді за таблицею - перетворення Фішера .

Знаходимо

, (5.0)

. (5.0)

Визначаємо при 95% рівні імовірності довірчі інтервали для :

; (5.0)

; (5.0)

. (5.0)

Скориставшись знову таблицями -перетворення Фішера, знайдемо тепер граничні значення для :

(5.0)

(5.0)

Отже

. (5.0)

Оцінка лінійного коефіцієнту кореляції є досить точною, а значить, тіснота зв’язку між роздрібним товарообігом та рівнем доходу громадян є дуже високою.

5.5 Побудова знайденої лінії регресії на одному графіку з вихідними даними

В кінці рішення задачі побудуємо на одному графіку вихідні дані та лінію регресії (рис.5.1):

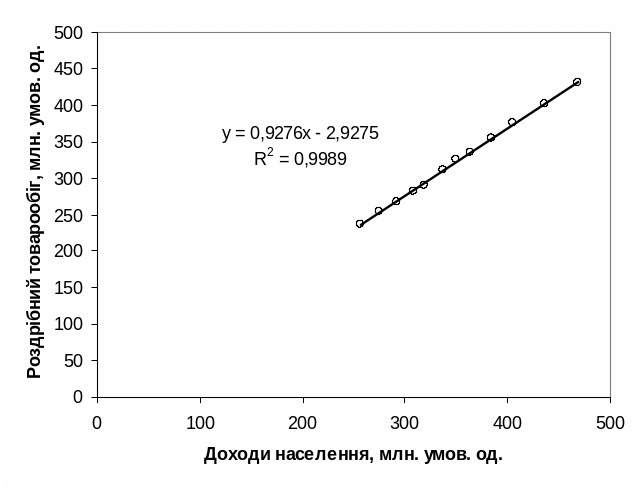
Рисунок 5.1 – Вихідні дані та лінія регресії

Висновок:

Побудована споживча функція має вигляд: . Розходження обґрунтованої та необґрунтованої складових дисперсії носить не випадковий характер і взаємозв’язок між рівнем споживання та рівнем доходу тісний. Високий лінійний коефіцієнт кореляції свідчить про тісний взаємозв’язок між роздрібним товарообігом та рівнем доходу. Знайдений довірчий інтервал не має значень 0 та 1, тому результати регресії відповідають якісній гіпотезі, згідно до якої , тому робимо висновок про достатню точність оцінки . До довірчого інтервалу входять як від’ємні, так і додатні значення, отже при 95% імовірності похибка при оцінюванні не істотно відмінна від нуля. Оцінка лінійного коефіцієнту кореляції є досить точною, а значить, тіснота зв’язку між роздрібним товарообігом та рівнем доходу громадян є дуже високою.