8

Лабораторная работа №2

Изучение туннельного эффекта и характеристик туннельного диода.

1. Цель работы: 1. Изучение прохождения микрочастиц через потенциальные барьеры (туннельный эффект, надбарьерное отражение).

2. Ознакомление с элементами зонной теории твердых тел.

3. Экспериментальное измерение вольтамперной характеристики (ВАХ) туннельного диода и определение его основных характеристик.

2. Приборы и принадлежности:

Источник напряжения, вольтметр, потенциометр, милли- и микроамперметр, перекидной двухполюсной ключ, туннельный диод.

3. Теоретическая часть

3.1. Туннельный эффект.

Пусть частица массы и энергии движется вдоль оси , и на своем пути встречает потенциальный барьер в виде прямоугольной ступеньки ширины и высоты (рис.1) т.е.

(1)

Рассмотрим вначале случай, когда . Явление прохождения частицы через потенциальный барьер, высота которого превышает ее энергию , называется туннельным эффектом. Основным количественным параметром, характеризующим этот эффект, является коэффициент проницаемости (прозрачности) барьера , который определяется как отношение потока частиц за барьером (область III) к потоку падающих на барьер частиц (область I, исключая отраженные волны). Для оценок параметра необходимо провести следующие расчеты:

а) для заданного потенциала (1) записать стационарное, одномерное уравнение Шредингера;

б) найти решения этого уравнения для всех трех областей ;

в) удовлетворить стандартным условиям, накладываемым на волновую функцию, в частности, условиям непрерывности и на границах областей:

; (2)

г) для полученных волновых функций вычислить плотность тока вероятности I и III согласно соотношению

. (3)

В частности, для волновых функций экспоненциального типа

; (4)

д) вычислить коэффициент проницаемости барьера .

Данная программа описана во всех руководствах по квантовой механике [1, 2], поэтому мы приведем лишь краткое описание этих этапов.

а) Динамика движения микрочастицы в одномерном потенциальном поле описывается стационарным уравнение Шредингера:

, (5)

которая для всех трех областей с потенциалом (1) приводится к виду:

, (6)

где введены обозначения

(7)

б) Решения уравнения (6) в общем виде имеют вид:

(8)

Решения имеют смысл падающих и отраженных плоских волн де Бройля (без временной зависимости). В силу однородности пространства за барьером (III область) отсутствуют отраженные волны, поэтому необходимо положить . Тогда с учетом соотношений (7), решения уравнения Шредингера окончательно можно представить в виде:

(9)

в) Для определения остальных коэффициентов и запишем граничные условия (2):

(10)

Решая однородную систему алгебраических уравнений (10), можно найти искомые коэффициенты , в частности:

. (11)

г) Так как падающие и отраженные волны имеют экспоненциальный характер, то в соответствии с формулой (4)

.

д) Отсюда для коэффициента проницаемости с учетом (11) окончательно получаем:

. (12)

Примем во внимание, что в большинстве задач микромира можно заменить на . Действительно, например, в атомной физике, полагая эВ, м параметр

и таким образом . Следовательно точную формулу (12) можно существенно упростить:

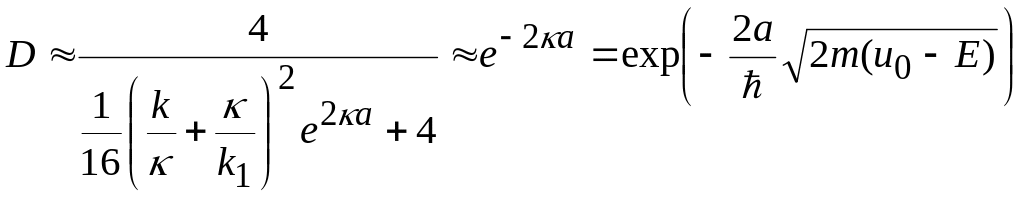. (13)

Следовательно с точностью до несущественного множителя перед экспонентой коэффициент проницаемости можно описать приближенной формулой (13).

3.2. Надбарьерное отражение.

В предыдущем пункте был рассмотрен случай, когда полная энергия частицы меньше высоты потенциальной ступеньки . Рассмотрим теперь движение частицы, когда . Очевидно и в этом случае уравнение Шредингера имеет прежний вид (6) с решениями (8). Однако параметр (7) становится действительным числом, при этом соотношение (12) сохраняет свой вид при замене на . С учетом очевидного условия

для коэффициента проницаемости получаем выражение вида:

. (14)

Из соотношения (14) следует, что частица беспрепятственно пролетает над барьером, как и в классическом случае , если (что физически свидетельствует об отсутствии потенциальной ступеньки , либо когда , что соответствует энергии (см.7)

, (15)

совпадающей с уровнями энергии в бесконечно глубокой потенциальной яме. В остальных случаях и частица испытывает так называемое надбарьерное отражение. Этот эффект также отсутствует в классической физике.

3.3. Элементы зонной теории твердых тел.

Как известно, энергия электронов в изолированном атоме образует дискретный ряд значений.

Рассмотрим свойство атомов, из которых образовано твердое тело в виде периодической пространственной решетки с периодом порядка размера атома и числом атомов (в реальном кристалле в 1м³ содержится атомов). Пусть вначале атомы расположены на больших расстояниях друг от друга . В этом случае электроны каждого атома отделены от областей соседних атомов достаточно широкими потенциальными барьерами, и их переход от одного атома к другому сильно подавлен. Так, при переход валентного электрона к соседнему атому осуществляется в среднем один раз за 10²⁰ лет. Следовательно энергия электрона в таком кристалле будет совпадать с энергией изолированного атома , который, однако, повторяется раз ( кратное обменное вырождение). При сближении атомов до реальных масштабов периодический потенциал , где потенциальная энергия электрона в изолированном атоме, поправка, учитывающая влияние соседних атомов. Это приводит в двум новым эффектам. Во-первых, появление дополнительного взаимодействия приводит к снятию обменного вырождения в кристалле, так что каждый кратно повторяющийся уровень атома расцепляется на близко расположенных подуровней, образующих т.н. энергетическую зону. Во-вторых, потенциальные барьеры уменьшают как ширину, так и высоту, и электроны получают возможность перемещаться по кристаллу за счет туннельного эффекта. Оценим качественно ширину энергетической зоны. Пусть электроны в кристалле имеют кинетическую энергию порядка энергии теплового движения: ( постоянная Больцмана, абсолютная температура). Теперь скорость их перемещения по кристаллу . Отсюда можно оценить время нахождения электрона в данном узле кристаллической решетки . Используя далее соотношение неопределенности для энергии и времени , для ширины энергетической зоны получаем: Дж~1эВ. Таким образом, в отличие от изолированного атома, энергия электрона в кристалле состоит из набора достаточно широких полос (энергетических зон), каждая из которых состоит из огромного, но конечного числа близко расположенных подуровней. Ширина зоны не зависит от размеров кристалла, а определяется природой атомов и их взаимным расположением.

В соответствии с принципом запрета Паули на каждом уровне зоны может разместиться не более двух электронов с противоположными спинами, число которых также ограничено в кристалле. Так как все физико-химические свойства атомов определяются внешними, валентными электронами, то наиболее существенными являются два типа зон:

а) Зона, соответствующая основным состояниям валентных электронов, называемая валентной зоной.

б) Ближайшая зона, соответствующая возбужденным состоянием валентных электронов, называемая зоной проводимости. Зона проводимости отделена от валентной зоны т.н. запрещенной зоной, в которой отсутствуют разрешенные уровни энергии (возможны варианты их взаимного перекрывания).

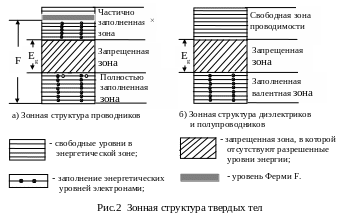
По характеру заполнения зон электронами все твердые тела можно разделить на две большие группы:

1. Тела, у которых над целиком заполненными зонами расположена зона, заполненная лишь частично, являются хорошими проводниками (в данном случае валентная зона и зона проводимости совпадают). Последний заполненный уровень энергии называется уровнем Ферми . При контакте двух металлов с различным положением уровней Ферми и 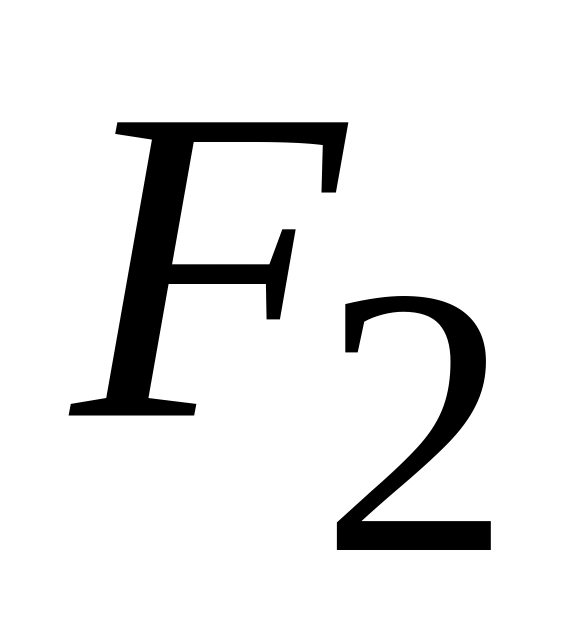происходит переход электронов из одного металла в другой до тех пор, пока уровни Ферми не выравниваются .

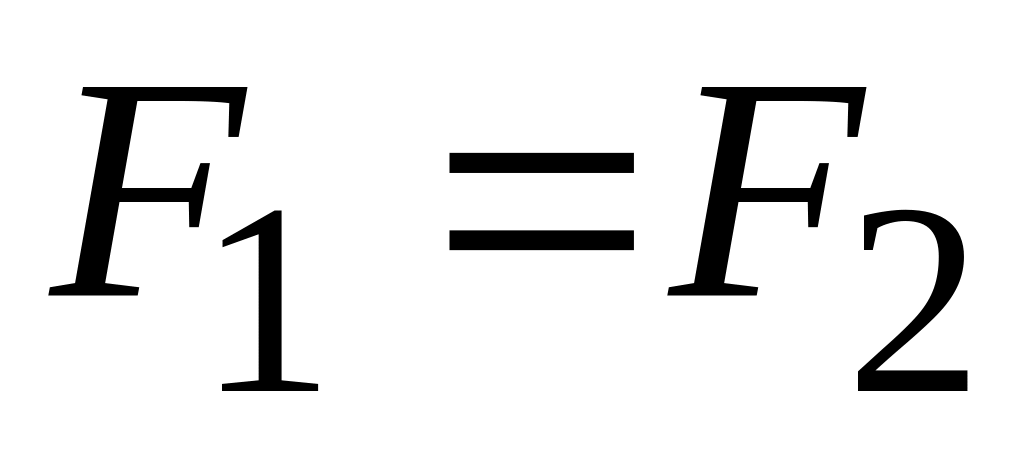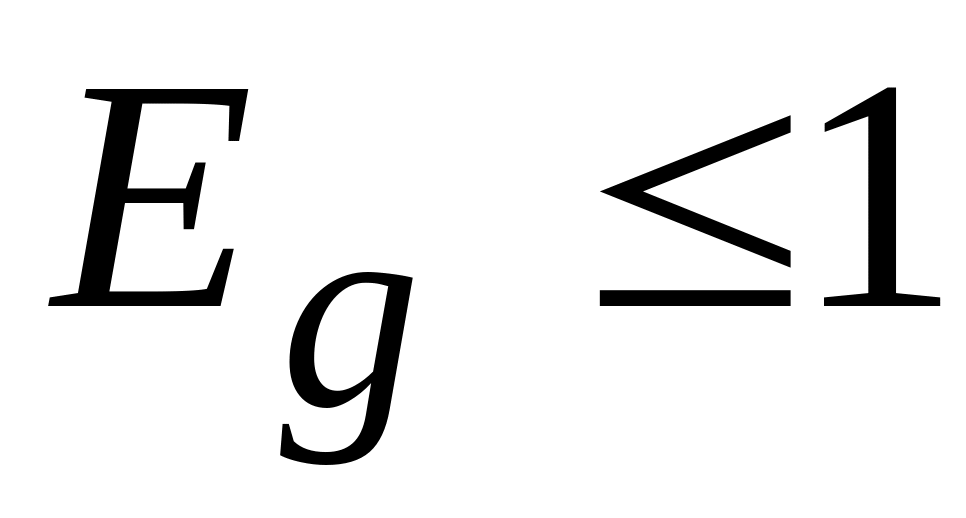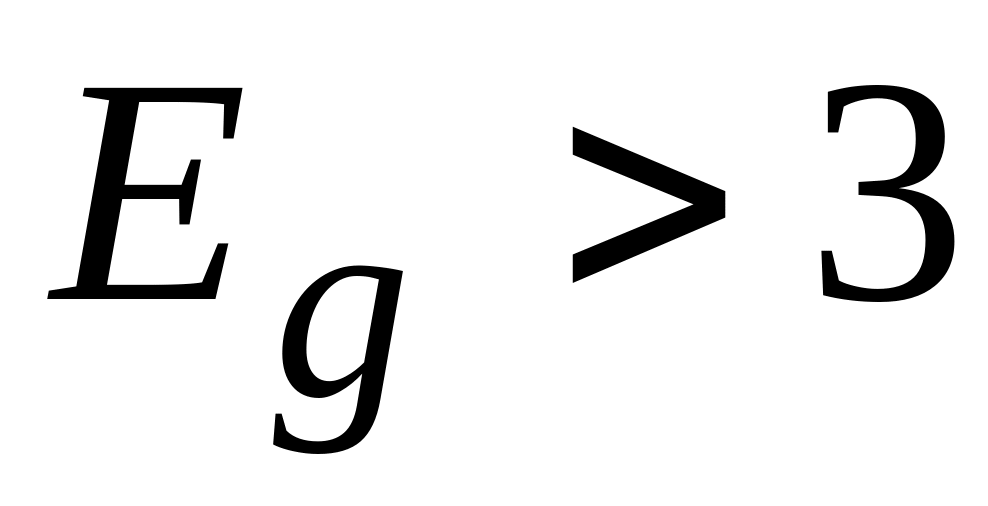2. Ко второй группе относятся тела, у которых над целиком заполненной валентной зоной расположена пустая зона проводимости (диэлектрики и полупроводники). Последние отличаются шириной запрещенной зоны (у полупроводников эВ, у диэлектриков эВ).

В отсутствии внешнего поля поток электронов слева направо компенсируется потоком электронов в обратном направлении и результирующий электрический ток в твердом теле . При включении электрического поля на каждый электрон действует сила , и они ускоряются или замедляются, т.е. изменяют свою кинетическую энергию, переходя в другие энергетические состояния. В системе нарушается равновесное распределение электронов по скоростям и возникает электрический ток. Однако, такие изменения возможны лишь в том случае, если в энергетической зоне имеются незанятые состояния, т.е. зона заполнена лишь частично (рис.2а). В случае кристаллов с зонной структурой, изображенной на рис.2б, это невозможно, и такие тела не могут быть хорошими проводниками. Если искусственно вызвать переход S-го электрона из валентной зоны в зону проводимости, то появляется нескомпенсированный ток с плотностью . Отсюда следует, что суммарная сила тока всех электронов валентной зоны, имеющей одно вакантное место, эквивалентно силе тока, обусловленное движением в ней одной частицы с положительным зарядом . Такую положительно заряженную фиктивную частицу назвали дыркой . Таким образом различают полупроводники типа, где основными носителями заряда являются электроны, и типа с основными носителями в виде дырок.

3.4. -переход в туннельном диоде.

Современные технологии позволяют получать полупроводники с наперед заданными свойствами путем введения специальных примесей (легирование) с высокой концентрацией примесей порядка 10²⁴м^-3. Предположим, что нам удалось создать два типа полупроводников и типа, таких, что уровень Ферми для электронов лежит в зоне проводимости для области и в валентной зоне для области (рис.3).

Зона проводимости

Зона проводимости

Уровень

Ферми F_n

Запрещенная зона













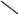
Запрещенная зона

Валентная зона



F_p

Валентная зона

























(n)

(p)

Рис.3 Зонная структура уровней p- и n-полупроводников.

Рассмотрим контакт двух таких полупроводников, между которыми образуется переходный слой ( переход) шириной порядка . Рассмотрим переход электронов через переход. Вследствие взаимной диффузии частиц электронные уровни в области поднимутся, а в области опустятся, переход будет происходить до тех пор, пока не выравниваются уровни Ферми . В зоне контакта в области из-за ухода электронов возникнет положительный заряд, в области – отрицательный. Электрическое поле этих зарядов приводит к возникновению на переходе потенциального барьера (рис.4), условно показанном на рисунке двойной штриховкой.

Если к переходу приложить внешнее поле в прямом направлении (минус к области, плюс  к области), т.е. противоположно внутреннему, то смещение зон уменьшится. Тогда часть занятых состояний в области будет находиться на одном уровне (перекроется) с незанятыми состояниями в области (рис.5). Следовательно, электроны из области смогут переходить на свободные уровни в валентной зоне области, но преодолеть барьер они смогут единственным способом  туннелированием. Если внешнее напряжение увеличивать, то будет увеличиваться и степень перекрытия занятых и свободных уровней и будет соответственно расти количество туннелирующих из в область электронов. Заметим, что перехода электронов из в область не произойдет, так как в области нет свободных уровней, следовательно, через контакт будет течь туннельный ток, возрастающий с ростом внешнего напряжения. При определенном напряжении степень перекрытия свободных и занятых зон достигнет максимума (рис.6) и при дальнейшем его росте начнет уменьшаться (рис.7). Соответственно и ток достигнет максимального значения и начнет уменьшаться. Это уменьшение будет проходить до тех пор, пока дно зоны проводимости области попадет в запрещенную зону области (рис.8), тогда туннельный ток полностью прекратится  частицам некуда переходить, нет соответствующих уровней энергии в области (рис.8).

При дальнейшем увеличении напряжения начнут перекрываться уровни зон проводимости обеих областей, потенциальных барьер уменьшится и возникнут условия движения частиц как на обычном переходе (рис.9).

Если на переходе подать обратное напряжение, то высота потенциального барьера возрастет, но возрастет и перекрытие зон. Теперь против свободных уровней области будут находиться заполненные уровни области (рис.10), следовательно, возникнет туннельный ток из в область  обратный ток диода. По мере роста обратного напряжения, растет перекрытие зон и обратный ток возрастает, т.е. туннельный диод не обладает односторонней проводимостью. Характерно, что обратный ток определяется движением основных носителей, в отличие от обычного диода. Полная вольтамперная характеристика туннельного диода приведена на рис.11.

Основными характеристиками туннельного диода являются:

пиковый ток (прямой ток в точке максимума вольтамперной характеристики);

ток впадины (прямой ток в точке минимума вольтамперной характеристики); отношение токов туннельного диода;

напряжение пика (прямое напряжение, соответствующее пиковому току); напряжение впадины (прямое напряжение, соответствующее току впадины);

напряжение раствора (прямое напряжение, большее , при котором ток равен пиковому;

среднее значение отрицательного сопротивления.

Наличие отрицательного дифференциального сопротивления у туннельных диодов позволяет применять их в схемах усилителей и генераторов, преобразователей и детекторов малых сигналов вплоть до сантиметрового диапазона длин волн, а также в импульсных схемах ЭВМ и устройствах автоматики. Более высокочастотные

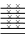
свойства туннельных диодов, по сравнению с «обычными» диодами обусловлены тем, что туннельный ток связан с движением основных носителей и поэтому явления наполнения и рассасывания неосновных носителей, ограничивающие свойства «обычных» диодов, у туннельных диодов отсутствуют.