Лабораторная работа № 8 Расчетные методы построения кривых ликвидуса
Цель работы: знакомство с методами построения кривых ликвидуса; построение диаграммы состояния двухкомпонентной системы.
Оборудование: калькулятор.
Основные понятия
Диаграммы состояния позволяют решать технологические задачи, связанные с синтезом силикатных материалов – стекла, керамики, вяжущих материалов: определять температурные интервалы возможной кристаллизации, составы эвтектик, кристаллических фаз в заданных условиях; оценивать плавкость систем; определять составы смесей для получения материала планируемого фазового состава с заданными эксплуатационными свойствами и т.д.
Существуют экспериментальные методы построения диаграмм состояния – динамический (получение кривых нагревания смесей и охлаждения расплавов) и статический (метод закалки) [1]. Но в ряде случаев в литературе отсутствуют данные по рассматриваемым системам, нет диаграмм состояния, то в этом случае прибегают к расчетным методам построения диаграмм состояния.
Используя законы химической термодинамики, можно определить температуру ликвидуса различных систем расчетным методом и построить их диаграммы состояния. Поскольку условием равновесия является минимум энергии Гиббса, каждая точка на диаграмме соответствует той фазе или совокупности фаз, энергия Гиббса которых меньше, чем у других возможных (конкурирующих) фаз в системе. Другими словами, для теоретического расчета и построения диаграммы состояния необходимо знание энергии Гиббса конкурирующих фаз при данных параметрах системы.
Энергии Гиббса конкурирующих фаз определяется из выражения ΔG=ΔH-TΔS на основании известных значений энтальпий (ΔH) и энтропий (ΔS) фазовых превращений компонентов, определяемых на основании экспериментального изучения термодинамических свойств веществ. Решая для различных задаваемых температур системы уравнений указанного типа для жидких и твердых фаз, находят их равновесные составы, т.е. геометрическое место точек кривых ликвидуса и солидуса на диаграмме Т – х.
Для двухкомпонентных систем можно рассчитать не только температуру ликвидуса, но и температуру, состав эвтектики. Расчетный метод применим только для систем, в которых между компонентами не образуются химические соединения.
Методика проведения работы
Существуют несколько методов построения кривых ликвидуса: по уравнению Шредера-Ле-Шателье, по уравнению Эпстейна-Хоуленда, по методу С.А.Суворова и др. [9].
Расчет кривых ликвидуса по уравнению Шредера-Ле-Шателье
Для расчета кривых ликвидуса двухкомпонентных систем используется уравнение Шредера-Ле-Шателье:
(8.1)
или
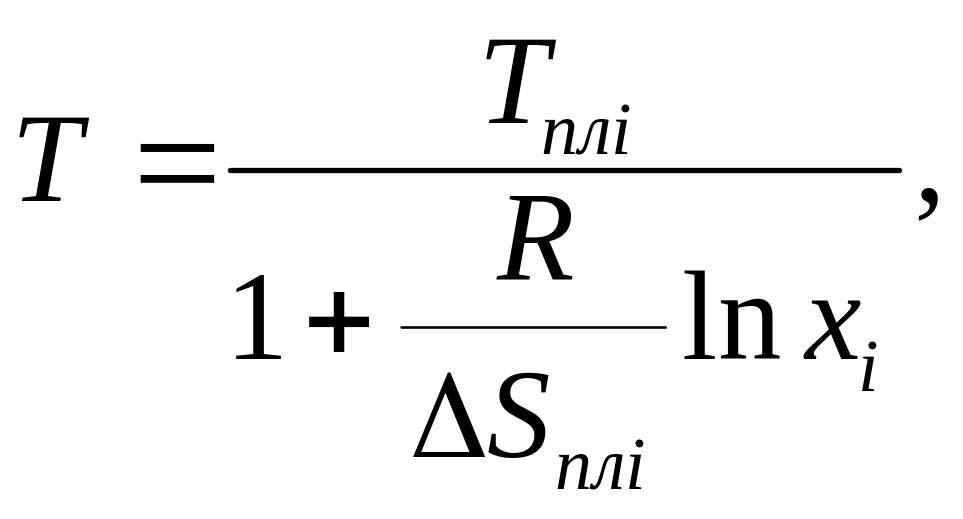(8.2)
где Т – температура ликвидуса, К; Tпл.i – температура плавления i-го компонента, К; R – универсальная газовая постоянная, равная 8,314 Дж/моль К; ΔS пл.i – энтропия плавления i-го компонента, Дж/моль; хi – молярная доля i-го компонента (хА + хВ =1).
Для исследуемых компонентов известны величины теплоты плавления ΔH, уравнение Шредера-Ле-Шателье будет иметь следующий вид:
(8.3)
(8.4)
или
(8.5)
(8.6)
где TА и TВ – температуры плавления компонентов А и В, К; ΔHА и ΔHВ - теплоты плавления компонентов А и В, кДж/моль К; хА и хВ – молярная доля компонентов А и В; TхА и TхВ – температуры ликвидуса соответственно при добавлении к компоненту А компонента В и наоборот, К.
По уравнениям (8.5, 8.6) строятся диаграммы плавкости двухкомпонентных систем, близкие диаграммам состояния, построенным на основании экспериментальных данных.