Линейная алгебра

Загрузка пакета >with(linalg):

Задание вектора

1) координатами >a: =vector([2,3,4]); a: = [2,3,4]

2) некоторыми первыми координатами с указанием размерности вектора

>b: = vector(4,[2,3]); b: = [2, 3, b3, b4]

Незаданные координаты b3 , b4 можно в дальнейшем вычислять или задавать

>b[3]:=2^3+4: b[4]:=2^5–1:

>print(b); вывести на экран вектор b [2, 3, 12, 31] .

3) Задание нулевого вектора >a:=vector(5,0); a:=[0,0,0,0,0].

4) Задание координат как функций от номера >a:=vector(3, x–>f(x)); a:=[f(1),f(2),f(3)].

(аргумент функции можно обозначать любой буквой).

Функцию можно задавать заранее:

>f:=n–>n^3;

>b:=vector(4,f); b:=[1, 8, 27, 64]

или

>h:=n–>diff(x^5,x$n);

>u:=vector(3,h); u:=[5x⁴, 20x³, 60x²] .

Примечание. n - ю координату вектора «а» можно вывести на экран командой >a[n];

Полностью любой вектор «а» выводится на экран командой >print(a);

Задание матрицы.

1) строками >A:=matrix([[1,2,3],[4,5,6]]); .

2) задать число строк (= 3) и число столбцов (= 2), а затем в квадратных скобках записывать через запятую элементы матрицы как строчки в книге

>A:=matrix(3,2,[1,2,3,4,5,6]); .

3) нулевая матрица, содержащая m строк и n столбцов, задается командой >A:=matrix(m,n,0);

4) единичная матрица n n задается командой >A:=array(1..n,1..n,identity);

5) матрица может быть задана функцией от номера строки m и номера столбца n

>F:=(m,n)–> 10*m+n:

>A:=matrix(2,3,F); .

Примечание. Для произвольной матрицы А можно вывести на экран командами

>A[m,n]; элемент m-й строки и n-го столбца ,

>row(A,n); полностью n-ю строку ,

>col(A,n); полностью n-й столбец .

Полностью матрица A выводится на экран командой >print(A);

Основные задачи линейной алгебры

1) Скалярное произведение двух векторов а и b

>dotprod(a,b);

Здесь векторы могут задаваться в форме >b:=[b1, b2, b3] , без слова vector.

2) Нахождение угла между векторами а и b

>angle(a,b);

Здесь векторы могут задаваться в форме >b:=[b1, b2, b3] , без слова vector.

3) Векторное произведение двух векторов а и b

>crossprod(a,b);

Здесь векторы могут задаваться в форме >b:=[b1, b2, b3] , без слова vector.

4) Нахождение базиса для произвольной системы векторов {a, b, c, d}

>basis({a, b, c, d});

5) Ортогонализация системы {a, b, c, d} линейно независимых векторов

>GramSchmidt({a,b,c,d}); [e1, e2, e3, e4] – система ортогональных векторов.

6) Норма вектора и его нормализация (координаты вектора делятся на его длину)

>a:=vector([3,4]); a:=[3,4] задание вектора,

>norm(a,2); 5 – норма (длина) вектора

>normalize(a); нормализация вектора, ответ: [3/5 , 4/5] .

7) Вычисление определителя квадратной матрицы А >det(A);

8) Сложение двух матриц или двух векторов одинаковой размерности

>add(A,B); A+B .

9) Линейная комбинация двух матриц или двух векторов одинаковой размерности

>add(A,B,m,n); mA+nB

10) Перемножение матриц подходящих размеров

>multiply(A,B,C);

11) Транспонирование матрицы А >transpose(A);

12) Для данной квадратной матрицы А вычисляется присоединенная матрица В (т.е. транспонированная матрица из алгебраических дополнений)

>B:=adj(A);

13) Вычисление обратной матрицы для квадратной матрицы А , если det(A)  0

>inverse(A);

14) Элементарное преобразование матрицы A: поменять местами m-ю и n-ю строки

>swaprow(A,m,n);

Аналогичная операция со столбцами осуществляется командой >swapcol(A,m,n);

15) Элементарное преобразование матрицы A: Умножение n-го столбца на число х

>mulcol(A,n,x);

Аналогичная операция со строкой производится командой >mulrow(A,n,x);

16) Элементарное преобразование матрицы A: столбец с номером m умножается на число х и прибавляется к столбцу с номером n

>addcol(A,m,n,x);

Аналогичную операцию со строками производит команда >addrow(A,m,n,x);

17) В матрице А выбирается ненулевой элемент A[m,n] и во всех строках над ним и под ним делаются нули при помощи элементарных преобразований

>pivot(A,m,n);

18) Вычеркивание из матрицы А столбцов с номерами от m до n

>delcol(A,m..n);

Если m=n , то удаляется только один столбец. Аналогичная команда для строк имеет вид

>delrow(A,m..n);

19) По данной системе S сформировать матрицу системы и расширенную матрицу системы

>S:=[2*x+3*y+4*z+5*t=6, x+y+z+t+a, x–y+z–t]; задание системы (отсутствие знака = означает равенство выражения нулю).

>V:=[x,y,z,t]; набор букв, которые принимаются за неизвестные,

>genmatrix(S,V); матрица системы,

>genmatrix(S,V,flag); расширенная матрица системы.

20) Приведение матрицы А к ступенчатому виду

>A:=matrix(3,3,[9,8,7,6,5,4,3,2,1]); 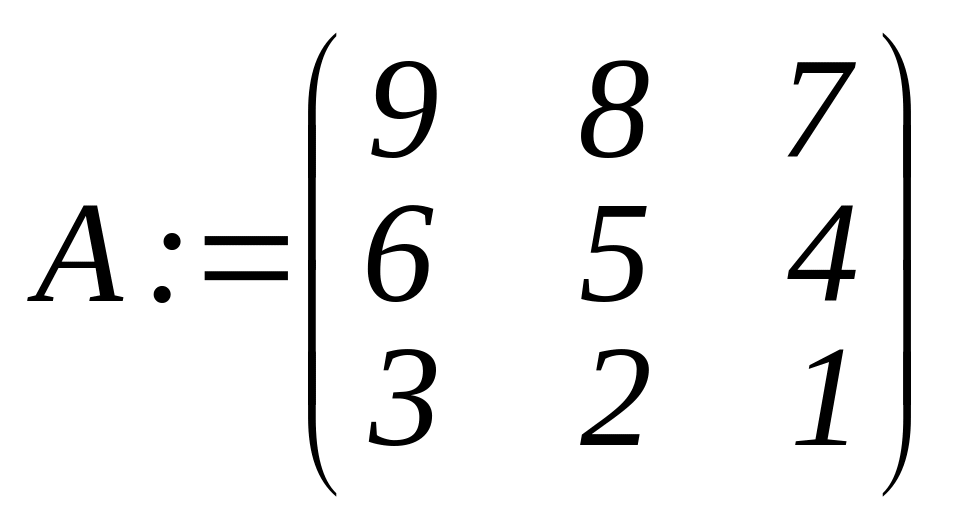задание матрицы.

>gausselim(A); (в ответе возможны дроби).

>ffgausselim(A); (в ответе дроби отсутствуют).

>gaussjord(A); приведение матрицы к главному ступенчатому виду.

21) Ранг матрицы А >rank(A);

22)Нахождение общего решения (с параметрами t1, t2, t3, …) для системы линейных уравнений с заданной расширенной матрицей А ступенчатого вида

>X:=backsub(A);

Пример.

>A:=matrix(2,5,[1,2,3,4,10,0,0,1,2,3]);

>X:=backsub(A); X: = [–2t₂+2t₄+1 , t₂ , –2t₄+3 , t₄].

Для получения какого-нибудь частного решения нужно придать свободным неизвестным (т.е. параметрам t2 , t4) какие-нибудь значения, например

>t2:=3; t4:=5;

и снова выполнить предыдущую команду >X:=backsub(A); получим X: = [5, 3, –7, 5] .

23) Решение линейной системы Ax=b (здесь вектор b задается без слова vector)

>linsolve(A,b);

Если система несовместна, то нет никакого ответа. При совместности выдается решение системы в параметрическом виде.

Матричное уравнение АХ=В решается такой же командой >linsolve(A,В);

Для решения матричного уравнения ХА=В нужно решить командой linsolve транспонированное уравнение А^ТХ^Т=В^Т и затем транспонировать результат. Если матрицы А и В квадратные, то уравнение ХА=В решается командой >X:=multiply(B,inverse(A));

24) Решение переопределенной системы Ах = b по методу наименьших квадратов

>A:=matrix(3,2,[2,3,1,1,1,-1]); задание матрицы А системы уравнений.

>b:=[4,2,3]; задание правых частей вектором b (можно без слова vector),

>leastsqrs(A,b); нахождение решения системы, ответ: [77/30, –2/5].

25) Нахождение характеристического многочлена для квадратной матрицы А

>P:=charpoly(A,lambda); (вместо  можно употребить любую другую букву). Команда вычисляет характеристический многочлен матрицы А.

Собственные числа матрицы А (корни этого характеристического многочлена) находятся затем командой

>solve(P,lambda);

26) Вычисление собственных значений матрицы А >eigenvals(A);

Ответ записывается в точном виде, если элементы матрицы заданы точно. Если же элементы матрицы заданы в десятичном виде, то собственные значения будут вычисляться приближенно.

27) Вычисление собственных значений (с указанием кратности) и соответствующих собственных векторов

>A:=matrix(2,2,[5,4,3,9]): задание матрицы А

>eigenvects(A); [3, 1, {[–2, 1]}] , [11, 1, {[1, 3/2]}] .

Здесь 3 – собственное значение , 1 – его кратность, [–2, 1] – собственный вектор.

28) Вычисление ротора векторного поля

>F:=[x*y, y*z, z*x]; задание пространственного векторного поля,

>u:=[x,y,z]; задание переменных, по которым будет вычисляться ротор,

>rotF:=curl(F,u); вычисление ротора, ответ: rotF:=[–y,–z,–x].

29) Вычисление дивергенции векторного поля

>F:=[x*y, y*z, z*x]; задание пространственного векторного поля,

>u:=[x,y,z]; задание переменных, по которым будет вычисляться дивергенция,

>divF:=diverge(F,u); вычисление дивергенции, ответ: divF: = y+z+x

30) Вычисление градиента скалярной функции

>F:=x*y*z; задание скалярной функции,

>V:=[x,y,z]; переменные, по которым будет находится градиент,

>gradF:=grad(F,V); вычисление градиента, ответ: gradF: = [yz, zx, xy].

31) Матрица Вронского от функций f(x), g(x), h(x) находится по команде

>A:=Wronskian([f(x), g(x), h(x)],x);

Определитель Вронского вычисляется затем по команде >det(A);

32) Нахождение потенциала векторного поля.

>f : = [P(x,y), Q(x,y)]; – задание векторного поля,

>potential(f,[x,y],’F’); – проверка поля на потенциальность (true, false) и вычисление

потенциала F векторного поля f ,

>F; – вывод потенциала на экран