§7. Функциональная последовательность. Предельная функция.

Характер сходимости.

В качестве образца разберем следующий пример. Пусть дана функциональная последовательность

.

Предельная функция U(x) находится по командам

>Un:=arctan(n^2*x/(n^2*x^2+1)); задание функциональной последовательности,

>U:=limit(Un,n=infinity): отыскание предельной функции.

Не исключено, что в ряде случаев предельная функция не имеет аналитического выражения. Поэтому вторая команда заканчивается двоеточием – предельная функция вычислена и записана в памяти, но не выводится на экран. График предельной функции строится затем по команде

>plot(U,x= – 3..3);

Для найденной предельной функции можно построить 2-окрестность (2-полосу)

>plot({U,U+0.2,U-0.2},x= –3..3); здесь  = 0,2 .

Можно построить семейство графиков функций U_n(x) , n=2..10

>plot({seq(Un,n=2..10)},x= –3..3);

Наконец, предельная функция, её 2-полоса и семейство функций U_n(x) изображаются на одном графике командой

>plot({ U,U+0.2,U-0.2, seq(Un,n=2..10)},x= –3..3,color=black);

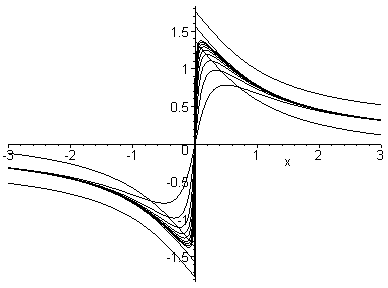
Вопрос. Можно ли утверждать, что начиная с некоторого номера п все кривые U_n(x) целиком попадут в 2-полосу? НЕТ! Следовательно, сходимость не является равномерной. Можно рассуждать по другому. Все функции последовательности U_n(x) непрерывны на всей числовой оси, а предельная функция разрывна. Следовательно, сходимость не является равномерной.

Динамику процесса можно наблюдать по команде >animate , подгрузив предварительно командой >with(plots): графический пакет.

>with(plots):

>animate({U,Un},x=-2..2,n=1..15,frames=100);

Видно, как кривая U_n(x) с ростом п «прижимается» к графику предельной функции.

§8. Дифференциальные уравнения.

1. Нахождение общего решения уравнения =f(x,y).

>eq:=diff(y(x),x)=f(x,y(x)); задание уравнения ,

>dsolve(eq); нахождение его общего решения.

Пример. Найти общее решение линейного уравнения xy’=y+x² cosx .

>eq:=x*diff(y(x),x)=y(x)+x^2*cos(x);

>dsolve(eq); y(x)=x sin(x)+x_C1 , где _С1 – произвольная константа.

Аналогичным образом решаются уравнения с разделяющимися переменными и с однородной правой частью. Для решения уравнения в полных дифференциалах Pdx+Qdy=0 следует подгрузить алгебраический пакет linalg.

>with(linalg): загрузка алгебраического пакета,

>H:=[P(x,y),Q(x,y)]; задание функций P(x,y) и Q(x,y) ,

>potential(H,[x,y],’f’); проверка условия полного дифференциала (true, false) ,

>f=C; нахождение общего решения в виде Ф(х, у)=С .

2. Решение задачи Коши =f(x,y) , y(x0)=y0 .

>eq:=diff(y(x),x)=f(x,y(x)); задание уравнения ,

>ic:=y(x0)=y0; задание начального условия,

>dsolve({eq,ic}); решение задачи Коши.

Пример. Решить задачу Коши y’=x+y , y(0)=2 .

>eq:=diff(y(x),x)=x+y(x);

>ic:=y(0)=2;

>dsolve({eq,ic}); y(x)= – x – 1 + 3e^x .

3. Уравнения 2-го порядка. Задача Коши.

Найти общее решение уравнения ay”+by’+cy=f(x).

>eq:=a*diff(y(x),x,х)+b*diff(y(x),x)+c*y(x)=f(x);

>dsolve(eq);

Найти решение задачи Коши ay”+by’+cy=f(x) , y(x0)=y0 , y’(x0)=y1 .

>eq:=a*diff(y(x),x,x)+b*diff(y(x),x)+c*y(x)=f(x); задание уравнения ,

>ic:=y(x0)=y0, D(y)(x0)=y1; задание начальных условий,

>dsolve({eq,ic}); решение задачи Коши.

4. Системы линейных уравнений.

Найти общее решение системы .

>sys:={diff(x(t),t)=a*x(t)+b*y(t),diff(y(t),t)=m*x(t)+n*y(t)};

>dsolve(sys);

Решить задачу Коши , x(t0)=x0 , y(t0)=y0 .

>sys:={diff(x(t),t)=a*x(t)+b*y(t),diff(y(t),t)=m*x(t)+n*y(t), x(t0)=x0, y(t0)=y0};

>dsolve(sys);

5. Поле направлений уравнения y’=f(x,y) .

Для построения поля направлений следует подгрузить пакет DEtools.

>with(DEtools):

>DEplot(diff(y(x),x)=f(x,y),y(x),x=a..b,y=m..n);

В правой части дифференциального уравнения вместо у(х) можно писать просто у , но обязательно нужно указать искомую функцию у(х) и области изменения переменных.

6. Собственные числа и собственные векторы.

При решении систем линейных однородных уравнений требуется находить собственные значения матрицы и собственные векторы. Для выполнения этих задач следует подгрузить алгебраический пакет linalg.

>with(linalg):

>A:=matrix([[0,2,3],[2,0,3],[3,3,5]]); задание матрицы A (по строкам),

>charpoly(A,lambda); нахождение характеристического многочлена ³ – 5² – 22 – 16

Нахождение собственных чисел (с указанием их кратности) и собственных векторов

>eigenvects(A);