Методические указания к лабораторной работе №4
Лабораторная работа №4 (далее – работа №4) содержит практические задания по теме лекции №4. Выбор варианта индивидуального задания – по номеру в списке академической группы.
Указания к выполнению работы №4. Работа №4 содержит задания по закреплению таких основных свойств отношений между элементами множеств как рефлексивность, симметричность и транзитивность.
При выполнении заданий необходимо использовать методики определения перечисленных свойств отношений, а также уметь строить их графические изображения и определять свойства отношений на графических множествах. При выполнении работы необходимо помнить, что отношения на множестве – это частный случай соответствия, и поэтому им присущи многие свойства соответствий.
Для обозначения отношения «параллельно» использовать символ ║ из меню «Добавить символ» ► «Набор: части рамок». Для обозначения отношения «не параллельно» использовать символ ╫ из того же меню.
Для обозначения отношения «перпендикулярно»
использовать символ
из редактора формул Microsoft
Equation. Для обозначения отношения «не
перпендикулярно» использовать символ
┬ из меню «Добавить символ» ► «Набор:
части рамок».
Для обозначения отношения «принадлежит» использовать символ •.
Вариант №1
Задание №1.
1. Даны выражения: 18+20; 40:8; 38; 50:10; 40-2. Используя отношение «равно», составьте все возможные истинные высказывания.
Задание №2.
1. Используя отношения «параллельно» и «перпендикулярно», составьте все истинные высказывания к рисунку 4.1.
Задание №3. Покажите на примерах, какие из следующих отношений: «равно», «больше», «меньше», «делится» – обладает свойством симметричности на множестве геометрических фигур.
Задание №4. Используя свойство транзитивности отношения на множестве, составьте третье высказывание и обоснуйте его истинность, исходя из данных двух:
(АВ) ║ (СД) и (СД) ║ (МЕ); 24х+1=у и у=20х+5.
Вариант №2
Задание №1.
1. Даны числа: 8, 13, 24, 17, 4, 9, 12. Используя отношение «больше», составьте все возможные истинные высказывания.
Задание №2.
Используя отношения «перпендикулярно» и «не перпендикулярно», составьте все ложные высказывания к рисунку 4.1.
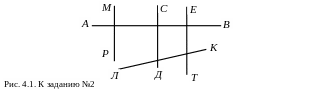
Задание №3. Покажите на примерах, какие из следующих отношений: «равно», «больше», «меньше», «делится» – обладает свойством симметричности на множестве натуральных чисел.
Задание №4. Используя свойство транзитивности отношения на множестве, составьте третье высказывание и обоснуйте его истинность, исходя из данных двух:
1. 3х+5=2 и 2=-3-5х; 2х+3=у и у=3х+1
Вариант №3
Задание №1.
1. Даны числа: 22, 11, 24, 15, 13. Используя отношение «меньше», составьте все возможные истинные высказывания.
Задание №2.
Используя отношения «параллельно» и «не параллельно», составьте все ложные высказывания к рисунку 4.1.
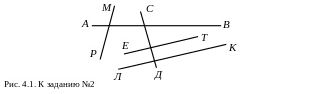
Задание №3. Покажите на примерах, какие из следующих отношений: «равно», «больше», «меньше», «делится» – обладает свойством транзитивности на множестве натуральных чисел.
Задание №4. Используя свойство транзитивности отношения на множестве, составьте третье высказывание и обоснуйте его истинность, исходя из данных двух:
1. ΔАВС = ΔОМД и ΔОМД = ΔРКЕ; 4х+2=у и у=5х.
Вариант №4
Задание №1.
1. Даны числа: 7+3; 10; 24-14; 14; 15, 24; 25. Используя отношение «равно», составьте все возможные истинные высказывания.
Задание №2.
Используя отношения «перпендикулярно» и «не параллельно», составьте все истинные высказывания к рисунку 4.1.
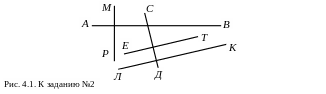
Задание №3. Покажите на примерах, какие из следующих отношений: «равно», «принадлежит», «параллельно», «шире» – обладает свойством транзитивности на множестве геометрических фигур.
Задание №4. Используя свойство транзитивности отношения на множестве, составьте третье высказывание и обоснуйте его истинность, исходя из данных двух:
1. ΔАВС > ΔОМД и ΔОМД > ΔРКЕ (отобразить графически); 3х+6=у и у=5х.