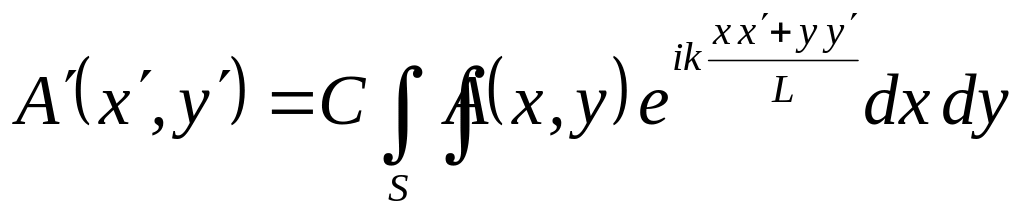Фурье-анализ

Из курса математического анализа известно, что если функция периодична с периодом , т.е. , то она может быть представлена в виде разложения в ряд Фурье

,

(*)

где - частота, и - коэффициенты разложения, определяемые как

(*)

Этот ряд можно представить в комплексной форме. Используя формулу Эйлера (*), выражение (*) можно записать как

,

(*)

где коэффициент разложения будет

.

(*)

При стремлении периода к бесконечности, что означает переход к непериодическим функциям, частоты, в силу соотношения , стремятся к нулю. При этом сумма (*) становится интегралом

.

(*)

где

.

(*)

Эти выражения для и представляют собой пару преобразований Фурье, причем для получения - прямое преобразование Фурье, а для - обратное. Функцию часто называют прообразом Фурье, а - образом.

Рис.*

Весьма важную роль при Фурье-анализе играет функция Дирака или так называемая - функция (дельта-функция). Она определяется двумя соотношениями

1. и 2. . (*)

	(*)
	(*)
	(*)

Эта функция является несколько необычной и определяется как предел. Таких предельных соотношений довольно много, приведем несколько из них (рис *).

где . На этом рисунке показан процесс деформации графиков функций при изменении параметра к предельному виду - -функции. При указанной зависимости функций от параметра значение интеграла от них остается постоянным и равным единице при любом, включая предельное значение , что фактически доказывает соотношения (*). Строгое доказательство этого обстоятельства можно найти в математической литературе. Дельта функция не является функцией в обычном смысле ее определения. Она относится к так называемым обобщенным функциям.

Отметим одно важное тождество, полученное на основе соотношения (*) и связанное с дельта - функцией

.

(*)

Основное и наиболее востребованное свойство ее представляется следующим соотношением. Если непрерывная функция, то

.

(*)

Это соотношение нетрудно доказать. с помощью определения функции как предел (*). Тогда

.

(*)

Теорема о среднем гласит, что если функция задана на отрезке , то на этом интервале найдется такая точка , что значение интеграла будет . В рассматриваемом случае , а , т.е. и в пределе, при , получится . Следовательно, значение искомого интеграла при подстановке и станет , что и требовалось доказать.

Таким образом, свертка с произвольной функцией дает значение этой функции в точке . Физическая интерпретация функции в теории электрических цепей представляет собой единичный импульс. Интеграл свертки (*) при этом является ее откликом на этот импульс, подаваемый на ее вход, т.е. выходным сигналом.

Операция преобразования Фурье в волновой оптике играет важную роль. При этом, однако, преобразования Фурье будут двумерными, поскольку распределения комплексных амплитуд, представляющих собой "предмет" и его "изображения"¹ являются двумерными и описываются функциями от двух переменных. Очень часто, однако, используются другие названия этих плоскостей (вообще поверхностей) – поверхность источников (ПИ) и поверхность анализа (ПА), поскольку оптические системы, особенно для лазерных систем, не всегда применяются для получения изображения, а часто используются для формирования световых пучков.

Интегралы преобразований Фурье будут иметь вид.

,

(*)

где и пространственные координаты, и так называемые пространственные частоты.

Часто такие двумерные интегралы записывают в виде, похожем на одномерные, только параметрами в них являются двумерные вектора – массивы из двух чисел , . При этом выражение для двумерного интеграла прямого преобразования Фурье будет иметь вид

(*)

где понимается как скалярное произведение. Обратное Фурье преобразование будет

.

(*)

По аналогии с одномерной - функцией можно ввести и двумерную - функцию соотношениями

1. 2. .

(*)

Соотношение же (*) будет иметь похожий вид

.

(*)

Использование преобразования Фурье в волновой оптике основано прежде всего на том, что основные дифракционные интегралы можно выразить через это преобразование. Показано. что дифракционный интеграл в приближении Фраунгофера или в дальней зоне, представляется интегралом Фурье (*)

(*)

где - волновое число, - распределение комплексных амплитуд в плоскости вторичных источников, - координаты в этой плоскости, - распределение комплексных амплитуд в плоскости, находящейся на расстоянии от нее (плоскости анализа), - координаты в этой плоскости, - несущественная константа, представляющая собой лишь общую энергию светового поля и никак не влияющая на структуру распределения. Эту константу в дальнейшем можно опускать, придав ее значение . Так как положение плоскости анализа в дальней зоне можно считать как в бесконечности, то такое же распределение будет и в оптически сопряженной с бесконечностью плоскости – фокальной плоскости некой линзы с фокусным расстоянием .

.

(15)

Распределение комплексных амплитуд в задней фокальной плоскости при этом будет

где , , - фокусное расстояние линзы, - координаты в задней фокальной плоскости линзы. Величины и по аналогии с преобразованием процессов во времени носят названия пространственных частот. Таким образом, линза осуществляет преобразование Фурье комплексной амплитуды светового поля, находящегося в передней фокальной плоскости.

В оптике двумерная дельта функция описывает точечный источник. В качестве примера рассмотрим прохождение светового поля через линзу от точечного источника, находящегося в передней фокальной плоскости. Пусть координаты точки и . Тогда распределение комплексных амплитуд в передней плоскости будет , а в задней фокальной плоскости получится как результат преобразования Фурье. Согласно определению - функции результат интегрирования будет

.

(*)

В

Рис.

показателе экспоненты находится линейная функция по , следовательно, это плоская волна. Сравнивая это выражение с уравнением наклонной плоской волны, распространяющейся в направлении вектора , найдем, что компоненты этого вектора будут , что полностью совпадает с геометрооптическим результатом (рис. *А)).

Если на линзу падает параллельный пучок, направляющий вектор которого , как и в предыдущем случае , то распределение комплексных амплитуд определится выражением

(*)

откуда следует, что в фокальной плоскости излучение сфокусируется в точку. Так как и определяются выражениями , , то координаты этой точки и будут и , что так же совпадает с геометрооптическим результатам (рис. Б)).

Следует отметить, что по логике, излучение в геометрическую точку сфокусировано быть не может, даже при идеальных, с точки зрения геометрической оптики оптических элементах (имеются в виду апланаты). Дело в том, что отсеченные выше соотношения справедливы лишь в параксиальном приближении, т.е. когда, во первых, с достаточной точностью можно считать, что , а во вторых, когда размер объекта по - крайней мере, больше половины длины волны. Другими словами "точка" как в случае А), так и в случае Б) – это объект порядка .

Дифракционный интеграл в приближении Френеля непосредственно может быть выражен через интеграл преобразования Фурье. Действительно если интеграл Френеля

,

(*)

где - координаты в исходной плоскости, - координаты в плоскости анализа, находящейся на расстоянии от исходной, - волновое число, представить как (разложив выражения в показателе экспоненты по формуле квадрата разности)

.

(*)

Полученное выражение представляет собой интеграл Фурье

,

(*)

где - множитель, не зависящий от переменных интегрирования, , , .

Преобразование Фурье применяется при решении многих оптических задач и не только в волновой оптике, но также и в геометрической. в частности что с его помощью находится так называемая оптическая передаточная функция, но это изучается в других разделах оптики.