Відлагодження алгоритму

В

ідлагодження алгоритму - систематичний процес іспиту алгоритму і вип­равлення що виявляються при цьому помилок.

При розробці алгоритму можуть допускатися синтаксичні помилки (по­ру­­шення правил запису алгоритму) і логічні помилки (порушення логіки рішення задачі). Локалізувати помилки в алгоритмі можна спеціальними методами:

 статичною перевіркою, що передбачає структурний аналіз керуючих кон­ст­рукцій алгоритму «вичитуванням» опису алгоритму з метою виявлення описок, недотримання відповідності типів даних у виразах, неузгодженістю фак­тичних і формальних параметрів модулів і т.п.;

 динамічною перевіркою (тестуванням) із метою виявлення відхилення дій­сних результатів від очікуваних.

Тест - набір вихідних даних, що дозволяє судити про правильність вико­нання алгоритму або його частин. Тест типу «білий ящик» основано на знанні внутрішньої структури алгоритму і полягає в перевірці роботи всіх блоків, кож­но­го окремо й у складі модулів. Тест типу «чорний ящик» передбачає пере­вірку еквівалентності вихідних даних їхнім описам і коректності функціонування мо­дулів для граничних значень параметрів.

Відомо, що модуль із 100 кроків містить 4..8 помилок, із яких приблизно 40% - алгоритмічні і 60% - помилки постановки задачі. Оскільки цілком уникнути помилок навряд чи можливо, прийнято вважати відлагодження успіш­ним, якщо у процесі відлагодження виявлено 50% алгоритмічних помилок.

«Якщо факти не підтверджують теорію, то їх треба позбутися» (Закон Майєрса) Етапи розв’язання задач на комп’ютері

Розв'язання задачі за допомогою комп'ютера потребує безмашинного і машинного опрацювання інформації.

Безмашинне опрацювання задачі займає приблизно 60...70 % часу, необ­хідного для її розв'язання, і містить у собі етапи:  - формалізація;  - вибір чи­сельного методу розв'язання;  - алгоритмізація;  - програмування.

Машинне опрацювання задачі полягає в обробці програми на комп'ютері за допомогою системи програмування.

Н

а цьому етапі задача моделюється математичними методами і будуються математична й інформаційна моделі.

Моделювання - дослідження об'єктів (явищ, процесів або систем) шля­хом побудови і вивчення їхніх моделей.

Модель - ідеальний або фізичний об'єкт (явище, процес або система), ана­­ліз і спостереження за яким дозволяє пізнавати суттєві риси іншого дослі­д­жу­ваного об'єкта.

Математична модель

Математична модель - модель, у котрій досліджуваний об'єкт подано у вигляді абстрактних величин і математичних співвідношень між ними.

Модель називають ізоморфною, якщо між нею і реальною системою існую повна поелементна відповідність. Модель називають гомоморфною, якщо від­по­відність існує лише між найбільш значимим складовими частинами об’єкта і моделі.

Функцією мети називають розрахункову характеристику моделі, що ви­значає необхідну її якість. Параметром функції мети називають вихідну вели­чину, необхідну для розрахунку значень функції мети. Областю визначення функції мети називається інтервал зміни її параметрів, для якого визначено формули розрахунку функції мети. Областю існування функції мети називає­ться інтервал її кінцевих дійсних значень.

У процесі побудови математичної моделі:

 - визначаються функції мети і їхні параметри; задача записується у вигляді математичних співвідношень, придатних для автоматизованої обробки даних, які вони містять;

 - чисельним аналізом математичних співвідношень виявляються обла­сті визначення й існування функцій мети; визначаються обмеження, що на­кладаються на ці області;

 - установлюються припустимі похибки чисельних розрахунків.

Наприклад, математична модель:

{

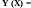описує залежність функції мети Y від параметра X. Область визначення функції обмежено множиною значень параметра X, що змінюється на сегменті [Xn; Xk]. Функцію не визначено при X=0. Областю існування функції мети є вся множина дійсних значень, за винятком значень Y (X = 5) і Y (X  -14).

У загальному вигляді математична модель об’єкта має функціональну специфікацію і представляється системою функціоналів: Ф (X, Y, Z, t) = 0, де: X, Y - вектори вхідних і вихідних координат, Z - вектор зовнішніх впливів, t - ко­ордината часу. Залежності між невідомими величинами фазових перемінних (X, Y, Z, t) і їхніми похідними визначаються з використанням різницевих мето­дів апрокси­мації. Засіб представлення Ф залежить від мети моделювання, при­зна­чення об'єк­та, обсягу інформації і характеру вихідних даних. По засобах пред­став­лен­ня математичні моделі підрозділяються на детерміновані і стохас­тичні, які у свою чергу класифікуються на безупинні і дискретні, аналітичні й імітаційні.

Детерміновані моделі

Поведінку більшості технічних систем можна охарактеризувати за допо­могою так називаних фазових змінних - фізичних величин типу потоку і потен­ціалу. При цьому доцільно виділити в об'єктах моделювання достатньо важливі елементи, розглянуті як неподільні одиниці. Закони функціонування елементів системи задаються компонентними рівняннями, що зв'язують різно­рідні фазові змінні. Спільність опису процесів, що відбуваються у різноманітних технічних системах, дозволяє виділити декілька типів елементів: R - елемент розсіювання енергії, С і L - елементи накопичення енергії. Сполученням цих найпростіших елементів і джерела фазових змінних одержують еквівалентну схему технічної системи будь-якої складності та її математичну модель. Сенс деяких фазо­вих змінних найпростіших елементів фізичних систем наведено у таблиці:

Підсистема	Фазові змінні		Элементи
	типу струму	типу потенціалу	типу Р	типу С	Типу L
Электрична	Струм	Напруга	Опір	Ємність	Індук­тивність
Механічна поступова	Сила	Швидкість	Тертя	Маса	Пруткість
. . .	. . .	. . .	. . .	. . .	. . .

Детермінована безупинна аналітична модель технічного об'єкта у зага­ль­ному випадку є системою звичайних диференціальних рівнянь. Подібну систему можна розв’язати тільки чисельними методами, замінюючи безупинну незалеж­ну змінну її дискретним аналогом. Ця операція визначає зміну безупинного типу моделі на дискретний тип.

Сукупність значень фазовий перемінних і їхній похідних на k-му кроці ін­тегрування утворюється як розв'язання системи n алгебраїчних рівнянь. (у зага­льному випадку нелінійних) із n невідомими Х₁, Х₂, ... , Хn:

f 1{ Х₁, Х₂, ... , Хn ) = 0;

f2{ Х₁, Х₂, ... , Хn ) = 0;

...... ...... ...... ...... ...... ...... ..

fn{ Х₁, Х₂, ... , Хn ) = 0;

Розв'язання такої системи рівнянь можливо ітераційними методами, найпоши­реним із який є метод Ньютона.

Стохастичні моделі

Стохастичні моделі за звичай мають додаткову процедурну специфіка­цію, що передбачає створення і використання алгоритмів (процедур) моделю­ван­ня об’єктів. Під час опису об'єктів виділяють такі види стохастичного (ймо­вірнос­но­го) моделювання.

Статистичне моделювання (що також називають методом Монте-Кар­­ло), окрім задач математичного моделювання, також застосовується при роз­в'я­зан­ні окремих задач чисельних методів, наприклад, узятті інтегралів чи роз­в'язанні диференціальних рівнянь. Статистичні моделі випадкових процесів мо­жуть бути реалізовані як на звичайних комп’ютерах (аналогових і цифрових), так і на спеціалізованих статистичних комп’ютерах, постачених моделюючими блоками для створення і перетворення випадкових чисел.

Аналітичне ймоврносне моделювання передбачає побудову моделей, що оперують не з конкретними випадковими числовими послідовностями, а без­по­середньо з їх ймовірносними (закони розподілу ймовірностей) і спектраль­ни­ми (спектральні щільності або кореляційні функції) характеристиками. У зага­ль­но­му випадку побудова аналітичних ймовірносних моделей являє собою склад­ну обчислювальну задачу, що не дозволяє повною мірою використовувати такої їх­ньої переваги, як можливість точного аналітичного задання характе­рис­тик ви­падкових процесів, відсутність необхідності генерації й опрацювання ве­ликих вибірок випадкових чисел, пристосованість до оперативної оптимізації. У літе­ратурі описано результати досліджень, спрямованих на створення спеціа­лі­зова­них проблемно-орієнтованих систем і пакетів прикладних програм, що об'єд­ну­ють чисельні алгоритми розв'язання найбільш характерних обчислю­ва­ль­них процедур аналітичного ймовірносного моделювання і засоби опису структур систем. Створення такого програмного забезпечення поряд із розробкою спеці­алізованих моделюючих комплексів дозволяє значно підвищити ефективність побудови і використання аналітичних моделей і, на цій основі, розв'язання задач стохастичного моделювання.

У поточний час основним методом стохастичного моделювання є метод статистичного моделювання на комп’ютері, що оперує зі стохастичними диск­ретними імітаційними моделями.

Методика статистичного моделювання включає ряд послідовних етапів:

- моделювання на комп’ютері псевдовипадкових числових послідовностей із за­даною кореляцією і законом розподілу ймовірностей, що імітують вхідні сигнали і обурюючі впливи у системі;

- моделювання перетворень отриманих числових послідовностей у системі;

- статистичну обробку результатів моделювання.