... Sk0 skj1 skj2 ... Qi sjk ... Skjr-1 skjr sk0 ...,  k[1;n]

по одному слову на кожну k-ту стрічку.

Така машина може переходити у наступний стан безпосередньо після та­ких дій:

 стан кожної поточної чарунки заміняється новим станом (він може спів­­падати зі старим);

 кожна стрічка зрушується на одну чарунку управо, уліво або ж залиша­ється нерухомою;

 внутрішній стан q_i пристою керування перетворюється у стан q_j, який може співпадати зі старим.

Задати програму багатострічкової машини - значить для кожного слова:

q_is_α1 ... s_αk (i  [1;n]; {α_j}_k  [1;n])

задати ябияку команду:

q_is_α1 ... s_αk  q_js_β1T₁ ... q_is_βkT_k, T  {Л, С. П}

Універсальна машина Тюрінга

До цього часу ми притримувалися тієї точки зору, що різні алгоритми здійснюються на різних машинах Тюрінга, які відрізняються набором команд, внутрішнім і зовнішнім алфавітами. Проте можна побудувати і універсальну машину Тюрінга, спроможну виконувати будь-який алгоритм.

В універсальній машині Тюрінга інформація також зображується симво­лами скінченого зовнішнього алфавіту, які розташовано на магнітній стрічці. Проте така машина повинна бути пристосована до сприйняття в якості вхідної інформації всіляких станив пристрою керування і конфігурацій, у яких можуть зустрітися літери із різноманітних алфавітів із якою-завгодно кількістю різно­ма­нітних символів. Це досягається шляхом кодування конфігурації і програми аби­якої даної машини Тюрінга в символах вхідного (зовнішнього) алфавіта уні­версальної машини.

Саме кодування повинно виконуватися у такий спосіб:

 різні букви повинні замінятися різними кодовими групами, але одна і та ж буква повинна замінятися усюди, де вона не зустрілася, однією і тією ж кодо­вою групою;

 рядки кодових записів повинні однозначним чином розбиватися на ок­ре­мі кодові групи;

 повинна мати місце можливість розпізнати, які кодові групи відпові­да­ють різноманітним зрушенням інформаційної стрічки, і розрізнавати кодові гру­пи, які відповідають буквам внутрішнього алфавіту і буквам зовнішнього алфа­віту.

Розгляньмо приклад такого кодування:

	Буква	Кодова група	Правило
Рух	Л	101	Один нуль
	С	1001	Два нулі
	П	10001	Три нулі
Зовнішній Алфавіт	S1	100001	Парна кількість нулів, більша 2
	S2	10000001
	. . .	. . .
	Sk	1(2·k+1 нулів)1
Внутрішній ал­фавіт (стан)	q1	1000001	Непарна кількість нулів, більша 3
	q2	100000001
	. . .	. . .
	qm	1(2·(m+1)+1 нулів)1

Так, наприклад, для машини Тюрінга, яке переробляє слово bcadc у сло­во bcdcc, вхідне слово з даним кодом буде подано рядком:

10000001 1000000001 100001 100000000001 1000000001,

, де 100001 - а, 10000001 - b, 1000000001 - c, 100000000001 - d.

Програма ж буде подана рядком:

1000001 10000001 1000001 10000001 101

1000001 1000000001 1000001 1000000001 101

1000001 100001 100000001 100001 101

100000001 100000000001 10000000001 1000000001 10001

10000000001 100001 100000000000001 100000000001 10001.

Таким чином, якщо яка-небудь машина Тюрінга розв’язує деяку зада­чу, то й універсальна машина Тюрінга може розв’язати цю задачу за умови, що ок­рім кодів вхідних наданих цієї задачі на її стрічку буде подано код програми.

Сучасні комп’ютери будуються як універсальні, а в запам’ятовувальний прист­рій, поряд із даними для поставленої задачі вводиться також і програма її роз­в’я­­зання. Проте, на відміну від машини Тюрінга, яка має необмежену зовніш­ню пам’ять (інформаційну стрічку), у будь-якому реальному комп’ютері пам’ять скінчена.

Для порівняння структур різних машин Тюрінга і оцінки їх склад­ності необхідно мати відповідну міру. Шеннон запропонував розглядати в якості та­кої міри критерій: «добуток кількості символів зовнішнього алфавіту і кіль­кості внутрішніх станів, відмінних від заключного».

Нарешті треба зазначити, що з математичної точки зору машина Тюрінга - просто визначений алгоритм для переробки слів, - тому математичні опера­ції композиції, виконувані над алгоритмами, дозволяють утворювати нові, більш складні алго­ритми з відомих простих алгоритмів.

Алгоритмічна система Маркова заснована на відповідності між слова­ми в абстрактному алфавіті і містить у собі об'єкти подвійної природи: элемен­тарні оператори й елементарні розпізнавачі. Елементарні оператори- опера­то­ри алфавіту, послідовне виконання яких реалізує будь-які алгоритми в аналізо­ва­­ній алгоритмічній системі. Елементарні розпізнавачі⁵ виконують розпізна­вання присутності тих або інших властивостей інформації, що переробляється алго­ритмом, а також для зміни (у залежності від результатів розпізнавання) по­слідовності виконання елементарних операторів. Для визначення множини еле­ментарних операторів і порядка їх виконан­ня у конкретному алгоритмі зручно користуватися особливими орієнтованими графами, які називають граф-схема­ми алгоритмів.

Граф-схема ал­го­ритму (її загальний вигляд наведено на мал. 1) являє со­бою скінчену множину вузлів, з’єднаних між собою відповідно наступним правилам:

 вузол «вхід» не має вхідних дуг (це позначається як Р⁺(х) = 0), але має одну вихідну дугу (Р^-(х) = 1);

 кожному вузлові, окрім «входу» і «виходу», зіставляєть­ся елементар­ний оператор або розпізнавач;

 у загальному випадку кількість дуг, що входять у вузол граф-схеми, мо­же бути до­вільною;

в окремому випадку (див. мал. 3):

- у кожний вузол, якому зіставлено елементарний розпізнавач, вхо­дить по дві дуги (Р⁺(х) = 2) і з кожного такого вузла виходить по дві дуги (Р^-(х) = 2);

- у кожний вузол, якому зіставлено елементарний оператор, в­хо­дить по одній дузі (Р⁺(х) = 1) і з кожного такого вузла виходить по одній дузі (Р^-(х) = 1);

 вузол «вихід» має одну вхідну дугу (Р⁺(х) = 1) і не має вихідних дуг (Р^-(х) = 0);

Вихід

Вхід

Р⁺(х) = 0

Р^-(х) = 1

Р⁺(х) = 1

Р^-(х) = 0

Р⁺(х) = 2

Р^-(х) = 2

Р⁺(х) = 2

Р^-(х) = 2

Р⁺(х) = 2

Р^-(х) = 2

Р⁺(х) = 1

Р^-(х) = 1

Р⁺(х) = 1

Р^-(х) = 1

Р⁺(х) = 1

Р^-(х) = 1

Граф-схема алгоритму

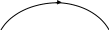
Мал. 3

Алгоритм, визначений граф-схемою, працює таким чином. Вхідне слово надходить на вхід і рухається по напрямкам, зазначеним стрілками. При влу­чен­ні слова в розпізнавальний вузол здійснюється перевірка умови, зіставленої вуз­лові. При виконанні умови слово спрямовується в операторний вузол, при неви­ко­нанні, - у наступний розпізнавач. Якщо вхідне слово р, яке подано на вхід граф-схе­ми, проходить через її вузли, перетворюється і кінець-кінцем потрапляє через скінчену кількість кроків на вихід, то враховується, що алгоритм можна за­­стосовувати до слова р (тобто слово р входить в область визначення цього ал­горитму). Результатом впливу на слово р буде те слово, що потрапляє до виходу граф-схеми. Якщо ж після подачі слова р на вхід граф-схеми перетворення і пря­­мування слова вздовжо граф-схеми продовжується нескінчено довго, не при­водячи на вихід, то враховується, що алгоритм не можна застосовувати до слова р (тобто слово р не входить в область визначення алгоритму).

У нормальних ал­горитмах в якості элементарного розпізнавача викорис­то­вується розпіз­на­вач входження, а в якості элементарного оператора - опера­тор підста­новки. Розпізнавач входження перевіряє умову «слово р входить у якості підслова у деяке надане слово q ?». Оператор підстановки заміняє пер­ше зліва входження слова р_i у слово q на деяке надане слово р₂. Оператор під­становки за звичай задається у вигляді: р_i р₂. Наприклад, для слова abcabca застосування підстановки bccb через два кроки:

 abcabca  acbabca

 abcacba  acbacba

призводить до слова acbacba. Послідовність слів p₁, p₂, ..., p_n, одержуваних у процесі реалізації алгоритму, називається дедуктивним ланцюжком.

Алгоритм, що задається граф-схемою, яку складено виключно з розпізна­вачів входження слів і операторів підстановки, називають узагальненим норма­ль­ним алгоритмом. При цьому передбачається, що до кожного оператора під­ста­новки веде лише одна дуга, що виходить із відповідного розпізнавача (Р⁺(х) = 1).

Нормальним алгоритмом називають такий узагальнений нормальний ал­горитм, граф-схема якого задовольняє наступним вимогам:

 всі вузли, що відповідають розпізнавачам, упорядковано за їхньою ну­мерацією від 1 до n.

 вихідні дуги вузлів, що відповідають операторам підстановки, під’єд­нуються або до вузла, відповідного першому розпізнавачу, або до вихідного вуз­ла. У першому випадку підстановка називається звичайною, у другому - заключ­ною.

 вхідний вузол під’єднується дугою до першого розпізнавача.

Нормальні алгоритми прийнято задавати упорядкованою множиною під­становок всіх операторів алгоритму (тобто схемою алгоритму). При цьому зви­чайні підстановки записуються у вигляді р_iр₂, а заключні підстановки - у виг­ляді р_i · р₂ (з точкою після стрілки). Процес виконання підстановок завершу­ється лише тоді, коли жодна з підстановок не застосовна до отриманого слова або коли виконано заключну підстановку.

Розгляньмо, наприклад, роботу нормального алгоритма Маркова, який задано алфавітом A = {+, 1} і системою підстановок: 1+111 та 1· 1 (граф-схему алгоритму наведено на мал. 4).

Нехай на вході задано рядок 11+11+1. Тоді наведеним алгоритмом його буде перетворено на рядок 11+11+11111+11111111111. Таким чином, алгоритм реалізує додавання одиниць.

Наявність у нормальних алгоритмах підстановок двох видів: звичайної і заключної є необхідною умовою універсальності нормальних алгоритмів, яка формулюється як принцип нормалізації: «Для абиякого алгоритму у довільному скінченому алфавіті А можна побудувати эквівалентний йому нормальний ал­го­ритм над алфавітом А».

На основі відомих нормальних алгоритмів можуть бути побудовані нові алгоритми шляхом застосування різноманітних засобів композиції алгоритмів:

 суперпозиції алгоритмів А і В, коли вихідне слово алгоритму А роз­гля­дається як вхідне слово алгоритму В;

 об’єднання алгоритмів А і В в алгоритм С, що перетворює абияке сло­во р, що міститься на перетинанні областей визначення алгоритмів А і В, в розта­шовані поряд слова A(p) i B(p).

Вихід

Вхід

Мал . 4

Наприклад, якщо задано: X = {a, b}, A = {ab  ba}, B = {ba  ab} і слово аbа із області перетинання, то: A(aba) = baa, B(aba) = aab, C(aba) = baaaab;

 розгалуження алгоритмів, тобто композиції D алгоритмів A, B і C, об­ласть визначення якої співпадає з перетинанням областей визначення алго­рит­­мів A, B і C, а для абиякого слова р з цього перетинання:

D(p) = A(p), якщо C(p) = e,

D(p) = B(p),

C(p)  e

, де е - порожній рядок.

Наприклад, якщо задано: A = {abba}, B = {baab}, C = {aba, ba e} в алфавіті X = {a, b}, то дії алгоритму D можна уявити як:

A(aba) = baa A(bab) = bba

B(aba) = aab B(bab) = abb

C(aba) = aa C(bab) = e

D(aba) = aab D(bab) = bba

 повторення (ітерація) являє собою комозицію С двох алгоритмів А і В. Для будь-яко­го вхідного слова р відповідне йому вихідне слово С(р) утворю­ється у резу­льтаті послідовного багатократного застосування алгоритму А до тих пір, поки не утвориться слово, що переробляється алгоритмом В в деяке фік­соване слово.

Наприклад, якщо задано: X = {a, b}, A = {abba}, B = {bbbaaab}, тоді C(ababb) = ab, оскільки: babbbaabbbababbbabbbbababbbaaab.

Важливе значення має можливість побудови складового універсального алгоритму, що може виконувати будь-які нормальні алгоритми; на його основі може бути побудовано універсальний комп’ютер.

Однією з особливостей абстрактної теорії алгоритмів є незмінність набору припустимих засобів побудови алгоритму і його виконання. Наприклад, усі час­тково рекурсивні функції утворюються з фік­со­ваного набору базисних функцій за допомогою операторів під­становки, при­мі­тивної рекурсії і найменшого коре­ня. Проте створення конкретних ал­горитмів потребує, щоби кожний алгоритм описувався у термінах своїх, най­більш зруч­них елементарніх засобів. Наприк­лад, алгоритм лінійної алгебри зруч­ніше опи­сувати за допомогою арифме­тич­них дій, а алго­ритм обліку функцій алгебри логіки - за допомо­гою ло­гічних опера­цій.

Тому першою вимогою, що пред’являється до алгоритмічної системи при практичному використанні алгоритму, є: «вигляд інформації, що переробля­є­ть­ся, і засоби її переробки повинні обиратися у залежності від класу алго­ритму».

У кожній класичній алгоритмічній системі список команд, що перетво­рю­ють вхідні надані на кінцевий результат, фіксується зазде­легідь і явно вказуєть­ся у запису алгоритму. Наприклад, список дій машини Тюрінга під час її робо­ти є незмінним. Проте можливість формування команд алгоритму у про­цесі його ре­алізації суттєво скорочує і спрощує запис алгоритму.

Тому другою вимогою, що пред’являється до алгоритмічної системи при практичному використанні алгоритму, є: «допускається формування команд алгоритму у процесі його виконання».

Розгляд реальних алгоритмів показує, що елементарні операції, які вироб­лено у процесі виконання алгоритмів, розпадаються на дві ариф­­­метичні і логіч­ні. Арифметичні операції перетворюють ін­формацію, а логічні визначають по­дальший напрямок обліку. Проте, логічні операції в кла­сичних алгоритмічних системах носять тривіальний характер. Наприклад, у машині Тюрінга логічною операцією є вибір напрямку руху інформаційної стрічки у залежності від стану машини і прочитаного символу. Така тривіаль­ність логічних операцій сильно ус­кладнює побудування конкретних алгоритмів.

Тому третьою вимогою, що пред’являється до алгоритмічної системи при практичному використанні алгоритму, є: «в алгоритмі допускається викори­с­тання універсальних логічних операцій».

Здебільше цим вимогам відповідають операторні алгоритмічні системи,

що й розглядаються далі.

Операторні алгоритми Ван Хао

Операторний алгоритм Ван Хао задається послідовністю наказів спеці­ального вигляду:

i

:

ω

α

β

Виконати такий наказ над числом х - значить знайти число ω(x) і далі: якщо ω(x) визначено, то перейти до виконання над ω(x) наказу з номером α; якщо ж ω(x) не визначено, то перейти до виконання над числом х наказу з номером β.

Наприклад, нехай:

x / 6 , якщо x = 24

ω(x) =

не визначено, якщо x  24

Тоді, якщо над числом x = 24 виконати наказ:

i

:

ω

7

12

, то одержимо число 4 і вказівку виконувати далі над числом 4 наказ із номером 7. Якщо ж виконати цей наказ над числом 23, то одержимо вказівку виконувати над числом 23 наказ із номером 12.

У термінах машини Тюрінга номера наказів відповідають номерам конфі­гурацій машини, а елементарна операція над об’єктом - елементарній дії над конфігурацією деякого стану.

Заключному стану машини Тюрінга відповідає наказ:

i

:

стоп

, який означає, що облік варто зупинити. Число, над яким виконується цей на­каз, є результатом обліку.

Програмою операторного алгоритму Ван Хао називається послідовність наказів:

i	:	ω	α		β
...	:	...	...		...
i + s	:	ωi+s	αi+s		βi+s
i+n	:	стоп

Якщо у результаті виконання алгоритму не буду здійснено переходу до на­казу «стоп», то результатом переробки x буде «невизначене значення».

Існує теорема Мінського, яка доказує, що «абияку частково рекурсивну фун­кцію можна обчислити за допомогою операторного алгоритму Ван Хао, якщо всі функції команд кодуються двійковими числами». Ця сентенція дозво­ляє реалізовувати програми операторних алгоритмів Ван Хао на універ­саль­них комп’ю­терах.

Операторні алгоритми Ляпунова

Алгоритмічна система Ляпунова, запропонована у 1953 р., стала од­нією з перших, що задовольняла усім вимогам до конкретних алгоритмів.

Для опису будови алгоритмів Ляпунов використав спеціальний матема­тич­ний апа­рат - так називані «логічні схеми алгоритмів». Логічна схема може містити:

 оператори - команди, що переробляють інформацію; спеціальний опе­ра­тор «ЗУПИНКА» позначає завершення роботи алгоритму;

 логічні умови, які перевіряються із метою визначення подальшого пе­ребігу виконання операторів алгоритму; при записі умов використовується за­га­льно прийнята символіка мате­ма­тичної логіки; наприклад, x < y позначає логі­чну умову, що може приймати зна­чен­ня «істина», якщоx дійсно менше, ніж y чи «брехня», якщо x не менше, ніж y;

 переходи, які використовуються для зміни порядку виконан­ня опера­то­рів алгоритму; вони позначаються ^N праворуч від логічної умови (тут N - уні­ка­льна позначка кожного напрямку переходу); оператор, до якого виконує­ться перехід, позначається поміткою ^N.

Логічна схема операторного алгоритму Ляпунова записується у при­род­ному порядку виконання операторів (зліва - направо) і завершується, якщо виконано оператор «ЗУПИНКА», або ж при відсутності в алгоритмі оператора, який повинен працювати далі.

Для запису алгоритмів використовуються оператори:

 арифметичні, що виконують арифметичні дії; вони позначаю­ть­ся за­го­ловними (великими) літерами латинського алфавіту, наприклад: А, В, С;

 перевірки логічних умов, що визначають порядок роботи команд алго­ритму; вони позначаю­ть­ся рядковими (малими) літерами латинського алфавіту, наприклад: p, q, s; якщо умова має значення «істина», то виконується наступ­ний оператор, інакше виконується оператор, який має відповідну помітку;

 переадресації, що:

- змінюють адреси у наказах;

- змінюють параметри, від яких залежить виконання операторі про­г­рами;

- відновлюють значення параметрі і адрес, які було змінено під час роботи алгоритму;

Оператори переадресації позначаються F(α), де α - адреса або параметр. Наприклад, F(i) збільшує і на 1, Fⁿ(i) збільшує і на n, F^-n(i) зменшує і на n і т.і..

 перенесення [α  β], що записує значення α у змінну β;

 формування, що ініціює початкові значення деяких параметрів чи роз­ташовує деякі зазделегідь визначені накази у визначені міс­­­ця алго­ритму. Опера­тор формування можна використовувати замість опера­тора переад­ресації, коли кількість переадресацій може бу­ти довільною, а початкове значення параметру завжди те ж саме. Наприклад, як­що початкове значення параметру і дорівнює s, то оператор формування може бути записано як {si}.

Розгляньмо приклад запису операторного алгоритму Ляпунова для під­сумовування п'ятьох чисел: а₁, а₂, а₃, а₄, a₅.

Нехай оператор A_i розраховує значення виразу c_і = c_i-1 + a_i, а параметр с розраховується як:

₅

с =  a_i

ⁱ⁼¹

Тоді операторний алгоритм Ляпунова для обліку суми має вигляд:

[1i] [0c_i-1] ^N A_i F(i) p(i=6) ^N ЗУПИНКА

Це позначає такі кроки алгоритму:

 Покласти i=1, c₀ = 0.

 Розрахувати c_і = c_і-1 + a_і.

 Збільшити і на 1.

 Перевірити, чи значення логічної умови i=6 є «істиною»; якщо ні, то пе­рейти до кроку , інакше зупинитися.

Блок-схемний метод алгоримізації передбачає розподіл усього обчис­лю­­вального процесу на окремі кроки, які позначаються графічними зобра­жен­ня­ми - «блоками». Блок-схемою алгоритму називається стандартизоване (див. ГОСТ 19.701-90) графічне зображення алгоритму, кож­ному кроку якого відпо­ві­дає блок. Звичайне співвідношення розмірів сторін блоку таке, що його довжи­на становить дві його висоти. Усі бло­ки, окрім блоків «Початок» і «Кі­нець», ну­ме­ру­ють­ по струмах зверху-донизу і зліва-на­право арабськими цифрами; номер ставлять ліворуч над блоком чи у розриві верхньої лініі блоку.

У блок-схемі може бути присутнім тільки один блок «Поча­ток», з якого починається абиякий алгоритм, і не менше одного блока-термінатора «Кінець», яким завершується виконання алгоритму:

Блоки «Введення» і «Виведення» використовуються для введення зна­чень нада­них, список ідентифікаторів яких вони містять усередині, із зовніш­ніх прист­роїв (клавіатури, файлу на дисці і т.і.) або виведення значень розра­хун­ко­вих даних на зовнішні пристрої (монітор, принтер, файл на дисці і т.і.):

Блок «Процес» (див. подальший малюнок, ліворуч) використовується для обліку даних за формулою, яку записано усередині блоку. Блок «Визначений процес» (див. подальший малюнок, праворуч) використовується для виклику на виконання підпорядкованого алгоритму:

Блок «Рішення» містить усередині умову, яка піддається сумніву; цей блок застосовується для організації розгалужень алгоритму.

Блок «Межа циклу» (типу «початок циклу» - ліворуч, типу «кінець цик­­лу» - праворуч) засто­совується для організації й обмеження циклів. Ініціююче значення пара­метру циклу (наприклад, X = X_n), його кінцеве значення (X_k), крок збільшення чи зменшення (X), або умова за­вершення циклу (X  X_k) записуються усередині початкового чи кінцевого блоку у залежності від типу циклу:

Блок «Модифікація» засто­совується для організації ітераційного циклу з передумо­вою і параметром, що змінюється з деяким кроком. Ініціююче зна­чення, кінцеве значення і крок збільшення чи зменшення параметру циклу запи­су­ють усередині блоку. Наприклад, запис X=X_n;X_k;X позначає зміну пара­метру X від початкового значення X_n до кінцевого значення X_k із кроком X:

Блоки у блок-схемі, як правило, мають один горизонтальний розмір, мо­жуть викреслюватися у будь-якій орієнтації і з'єднуються лініями потоку. Ці лі­нії повинні бути спрямовані до центру блоку і, за звичай, підходять до нього зверху або ліворуч, а виходиять з нього знизу або праворуч. Лінії потоку закін­чу­ються стрілкою, якщо блоки, що з'єднуються, виконуються у напрямках «лі­во­руч» чи «нагору», або ж лінія потоку перетерплює злам. Декілька ліній потоку можуть з'єднуватися в одну, причому місце з'єднання звичайно зсовується:

Абиякий блок можна коментувати; для цього праворуч чи ліворуч від нього накреслюють блок «Коментар» (див. подальший малюнок, ліворуч).

Частини блок-схеми на різних аркушах паперу з'єднуються за допомогою блоку «З’єднувач», усередині якого записується унікальна позначка (див. пода­ль­ший малюнок, праворуч).

HIPO (Hierarchy-Input-Process-Output⁶) - технологія алгорит­мізації, яка ви­користовується для побудови алгоритмів обробки інформації у склад­них (як правило корпоративних) інформаційних системах і передбачає побудову двох типів схем:

 схеми «ієрархії», яка являє собою схему підпорядкованості алгорит­мів розв’язання підзадач основної задачі:

 схем «Вхід - Процес - Вихід» (для кожного алгоритму схеми «ієрар­хії»), що використовують сиволіку блок-схемного методу алгоритмізації і пока­зують джерела наданих, засіб іх опрацювання і приймачі результатів обліку:

Алгоритм 2.1 «Облік прибутку Східного відділку банку «Зевс»»
Вхід	Процес	Вихід	Примітка
	Крок 1. V = 5·X - sin(X)		Облік відсотку прибутку за рік
. . .	. . .	. . .	. . .

«Складність програми зростає доти, поки не перевищить здібностей програміста»

(закон програмування)

Оцінка алгоритмів

Методи оцінки складності алгоритмів

В теорії алгоритмів поняття «алгоритм» за звичай уточнюється за допо­мо­гою опису «математичної моделі» обчислювальної машини. Тут мож­ливі два підходи в залежності від того, чи оцінюється складність алго­ритму (маши­ни, програми) або складність обліку, що протікає від­по­відно до алгоритму.

В якості міри складності алгоритмів розглядається функціонал, котрий спів­­відносить кожному алгоритму А деяке число μ(А), що характеризує його громіздкість (наприклад, число команд в А, довжину запису А або ж будь-яку іншу чисельну оцінку обсягу інформації, що міститься в А). Подібні функціо­на­ли давно застосовуються в теоретико-кібернетичних дослідженнях схем, що ре­алізують функції алгебри логіки (Шеннон, Яблонский, Ляпунов та ін.), а також в обчислювальній математиці, де потужність схеми, за якою обчислюється ба­га­точлен, вимірюється кількістю арифметичних операцій, що фігурують у схемі. Різниця полягає лише в тому, що в зазначених роботах розглядаються спеці­аль­ні вузькі класи функцій і спеціальні засоби опису алгоритмів.

В теорії ж алгоритмів необхідна розробка і застосування аналогічних по­нять для більш загальнихй ситуацій (будь-яких обчислюваних функцій, загаль­них концепцій алгоритму). Перші публікації, у яких такі міри складності знайш­ли застосування, належать Маркову й Колмогорову. К цих роботах в якості міри складності алгоритму розглядається функціонал, що спів­від­­но­сить кожній парі (А, а) деяке число (А, α) (тут А - алгоритм, α - індиві­дуа­ль­на зада­ча з того кла­су задач, що алгоритм А розв’язує). Це число характе­ризує склад­ність роботи всього алгоритму А від вхідних даних α до видачі ре­зультату. На­приклад, в якос­ті (А, α) можна брати кількість елементарних кро­ків, із яких складається алгоритм або обсяг пам'яті, що може знадобитися для реалізації усіх операцій під час перебігу процесу обліку і т.і. Оскільки для кож­ного алго­ритму А одно­значно визначено клас задач , що він вирішує (наприк­лад, функ­цію мети f), то можна вважати, що кож­ний алгоритм А характери­зуєть­ся функ­ці­єю змінної α:

α _А(α) = (А, α)

^df

Іншими словами, можна вважати, що мірою складності роботи алгоритму є опе­ратор, що зіставляє з кожним алгоритмом А відповідну функцію _А(α). За зви­чай вважають, що міра складності алгоритму приймає лише нату­ра­льне значен­ня, тому для кожної обчислюваної функції існує алгоритм її обліку з мініма­ль­ною складністю. Цю мінімальну складність природно розгля­дати як складність самої функції, тим самим і множина усіх залежних функцій упоряд­ко­вана по сту­пеням складності цих функцій.

Якщо ж вхідною є міра складності обліку, то утворюється інша картина. Дві сигналізуючі функції _А і _В, можуть виявитися непорівнянними, навіть як­що вважати _А < _В. Тому, якщо зафіксовано деяку функцію мети f, то апріорі не ясно, чи існує для неї найкращий облік. Тут доводиться обмежувати­ся більш слабкою характеристикою складності самої функції f, іншими словами дово­ди­ться шукати функції: φ₁ (нижня оцінка) і φ₂ (верхня оцінка), такі, що:

 існує алгоритм А обліку f із сигналізуючою, що не перевищує φ₂;

 який би не був алгоритм А обліку f, його сигналізуюча не менша ніж φ₁.

Зрозуміло, що чим ближче одна до одної верхня і нижня оцінки φ₁ і φ₂, тим точ­ніше охарактеризовано складність самої функції f.

Теорія складності залежить від покладених в її основу концепцій алгорит­му (рекурсивні функції, машини Тюрінга і т.і.), а також від обраної міри склад­ності. Можна було б припустити, що при переході від однієї концепцій алгорит­му до іншої необхідно наново будувати теорію складності. Проте ідея моделю­ван­ня одних алгоритмів іншими позбавляє нас від цього.

Розгляньмо оцінку складності алгоритму стосовно до машин Тюрінга. З кожною конфігурацією k, до якої застосовано машину Тюрінга, можна асоцію­вати число, що характеризує складність процесу М(k). Варіюючи k, одержимо функцію від неї, визначену на множині усіх кон­фігурацій, до яких дана машина застосовна. Функції такого роду називають си­г­налізуючими функціями.

Роботу машини М будемо характеризувати наступними си­г­налізуючими функціями:

Сигналізуюча часу t_m(k) дорівнює тривалості процесу М(k) (тобто кілько­с­ті його конфігурацій), якщо М застосовна до k і не визначена в іншому випад­ку. Активною зоною процесу будемо називати мінімальну частину стрічки, що обіймає активні зони всіх його конфігурацій. Активною зоною кон­фігурації будемо називати мінімальну зв'язкову частину стрічки, що містить ог­ля­даєму ча­рунку і всі чарунки, в яких записано значущі літери.

Сигналізуюча ємності s_м(k) дорівнює довжині активної зони процесу М(k), якщо М застосовна до k, і не визначена в іншому випадку.

Сигналізуюча коливань ω_м(k) дорівнює кількості коливань (зміни напрям­ків) голівки за час t_м(k), якщо М застосовна до k, і не визначена в іншому випад­ку.

Сигналізуюча режиму r_м(k) дорівнює максимальній кількості проходжень голівки через край чарунки за час t_м(k), якщо М застосовна до k, і не визначена в іншому випадку.

Зокрема, якщо в якості конфігурацій k узято початкові конфігурації для слова р, то процес буде характеризуватися сигналізуючими функціями t_м(р), s_м(p), ω_м(р), r_м(р). Поряд із ними розглядаються і функції типу:

t⁽ⁿ⁾_m = max tm(p), ω⁽ⁿ⁾_m = max ω _m(p), s⁽ⁿ⁾_m = max sm(p), r⁽ⁿ⁾_m = max rm(p),

, де |p| - довжина слова р ( |p| = n), а також функції типу:

t*_m (n) = max tm(γ); ω*_m (n) = max ω _m(γ);

s*_m (n) = max sm(γ); r*_m (n) = max rm(γ),

, де γ - найбільше з довжин слів р_i ( γ < n).

Побудова машини дає лише верхні сигналізуючі оцінки. Знаходження ж нижніх оцінок є більш складною справою і потребує спеціальної теорії. Має міс­­це теорема, що показує, що при наявності верхньої оцінки, для будь-якої з сигналізуючих (t, s, ω, r) і даних параметрах m и n (m - кількість сим­волів зов­нішнього алфавіту, n - кількість символів внутрішнього алфавіту) можна одер­жати верхні оцінки для інших.

Теорема. Для будь-якої машини М и для будь-якого слова р, до якого вона застосовна, справедливі такі нерівності:

ω(p)  t(p), r(p) ω (p) + 1, s (p)  |p| + 2nr^(p)+1 , t(p)  m^s(p) · s(p) · n