Блок-схеми алгоритмів інтерполяції і апроксимації функції

поліномами Лагранжа B-сплайнами

1

1

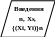
2

2

3

3

6

9

4

4

5

6

8

8

5

Так

Ні

7

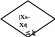
Ні

7

Так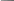

Мал. 28

Алгоритм статистичної обробки результатів експерименту

При розв'язанні задач ідентифікації, оптимального керування і т.п., а та­кож у процесі виконання практичних вимірів часто необхідно не тільки знахо­ди­ти похибку спостереження, але і давати оцінку похибки результатів експе­ри­мен­ту. Наприклад, для ігнорування грубих похибок необхідне попереднє статис­тичне опрацювання результатів вимірів, у загальному випадку розглядаються як випадкові значення.

Випадковим називається така подія, що при виконанні визначеного комп­лексу вимог може або відбутися, або не відбутися. Таким чином можна вважати, що при проведенні повторних експериментів в тотожних умовах кожна з мно­жи­­ни можливих незначних причин випадкових результатів спостережень може з'явитися або не з'явитися, може приймати всякі значення як за значенням, так і за знаком.

Для кожного i-го спостереження Xi випадкова абсолютна похибка роз­ра­ховується за формулою Xi = X - Xi , де Xi - дійсне значення вимірюваного па­раметру.

Теоретично доведено, що якщо закон розподілу значень випадкового па­раметру є нормальним (у більшості випадків це так) і систематична похибка цілком виключена, то дійсне значення вимірюваного параметру дорівнює мате­матичному очікуванню результатів виміру. Математичне очікування випад­кової величини - це таке її значення, біля якого групуються результати окремих вимірів. При обмеженій кількості в N наглядів результати наглядів характери­зу­ються оцінками параметрів функції розподілу випадкової.

Оцінкою математичного очікування M [x] є середнє арифметичне:

1 _N

X = —— •  Xi.

N ⁱ⁼¹

Мірою розсіяння значень випадкової є дисперсія D[x], оцінка D якої вира­жається формулою:

1 _N _

D = —— •  (Xi - X )².

N-1 ⁱ⁼¹

Міру розсіяння також характеризують середньоквадратичним відхилен-ням S[x], яке оцінюється за формулою  = D. Оцінку приписують кожному з N результатів наглядів і називають похибкою одного нагляду, стандартним від­хиленням або стандартом.

Для перевірки виду похибки і відкидання аномальних наглядів викорис­то­ву­ють критерій:

1 _

Vi =  • (X - Xi).



Якщо, наприклад, для N=20 виконується Vi > 2,71 (із вірогідністю 0,025), то ре­зультат i-го нагляду називається грубою похибкою і відкидається як аномаль­ний.

Мірою зв`язку між двома множинами {X1} і {X2} експериментальних на­даних є коефіцієнт кореляції:

_____ __ __

X1• X2 - X1• X2

r = ———————.

_X1 • _X2

Коефіцієнт кореляції може приймати значення у межах [-1; +1]. Значення мо­дуля коефіцієнта кореляції, яке дорівнює 1, свідчить про функціональну залеж­ність між даними множин, а нульове значення - про повну взаємну незалеж­ність елементів множин.

Алгоритм статистичної обробки результатів експерименту є досить три­ві­альним, тому його пропонується скласти самостійно.