Блок-схеми алгоритмів розв’язання диференціальних рівнянь першого порядку

Метод Ейлера Метод Рунге - Кутта

2

6

Мал. 23

3

5

Ні

Так

5

1

3

Ні

Ні

4

Так

4

7

6

1

2

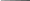
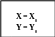
Блок-схеми алгоритмів розв’язання диференціальних рівнянь другого порядку

Метод Ейлера Метод Рунге - Кутта

1

2

6

3

5

Ні

Так

5

1

2

3

Ні

Ні

4

Так

4

7

6

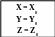
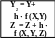
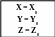
Мал. 24

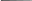
Алгоритм обліку визначеного інтегралу

У задачах, що пов'язані з аналізом, ідентифікацією, оцінкою якості, мо­де­люванням різноманітних пристроїв автоматики, керування, інформаційно-ви­мірювального техніки, радіоелектроніки, виникає необхідність обліку визначе­них інтегралів. Найпростішим прикладом може виступати оцінка якості керу­ван­ня за допомогою інтегральних оцінок якості:

_{b b}

I =  f(t)• dt або I =  f ²(t)• dt (a = 0, b  ),

^{a a}

я кий мають на меті дати загальну оцінку швидкості загасання і значення відхи­лення керованої змінної у сукупності, без визначення того або іншого відхи­лен­ня окремо (тут f(t) - відхилення керованої величини від нового сталого значен­ня, що вона буде мати після завершення перехідного процесу). У сталій системі при f  0 і t   (t - час) цей інтеграл має скінчене значення. У ряді випадків, якщо підінтегральна функція f(x) безперервна у межах [a; b], точний облік ін­те­г­рала за відомою формулою Ньютона - Лейбниця буває утрудненим великою склад­ністю аналітичного визначення першообразної. У розповсюдженій зада­чі, коли підінтегральна функція задається таблично (масивом значень), поняття першо­об­разної взагалі не має сенсу, і інтеграл може бути знайдено тільки чи­се­льно з використанням комп'ютера. Задача чисельного інтегрування функції по­ля­гає у розрахунку значень визначеного інтеграла на основі ряду значень під­ін­теграль­ної функції. Графічно інтеграл визначається площею, що обмежена графіком функції Y = f(X), віссю абсцис і перпендикулярами до неї у межах ін­тегрування [a; b] (мал. 25).

Мал. 25

Алгоритм до методу Ньютона - Котеса

Найбільш відомим серед використовуваних на практиці мето­дів обліку ви­значених інтегралів є метод Ньютона - Котеса. Метод полягає у роз­­поділі інтер­валу інтегрування [a; b] на k рівних підінтервалів X і заміщенні підінтег­раль­ної функції на кожному з них інтерполяційним поліномом Лагран­жа:

_{X2 k}

I =  f (x) • dx = (b - a) •  H_i • f (X_i), (1)

^{X1 i=0}

для k рівновіддалених вузлів інтерполяції {X_i}_k із кроком X = (b - a) / k і з точ­ніс­тю  (у формулі (1) Hi - коефіцієнти Котеса).

Якщо n = 1, то коефіцієнти Котеса складають: Ho = H₁ = 1 і формула (1) зводиться до формули трапецій:

I = X • [ f(X_i) + f(X_i+1) ] / 2.

Якщо ж n = 2, то коефіцієнти Котеса складають: Ho = 1, H₁ = 4, Н₂ = 1, а форму­ла (1) зводиться до формули параболічних трапецій для 2 • k підінтервалів:

I = X • [ f(X_i) + 4• f(X_i+1) + f(X_i+2) ] / 3.

Оскільки коефіцієнти Котеса для великих значень n є досить складними, то для прак­тич­ного наближеного розрахунку визначеного інтеграла інтервал розбива­ється на велику кількість малих інтервалів і до кожного з них застосовується формула Ньютона - Котеса з малим значенням n (n = 1 або n = 2). Отримані фор­­мули ма­ють більш просту структуру, а їх точність залежить від кількості під­інтервалів інтегрування і може бути довільно високою.

Нижче наведено алгоритм розрахунку визначеного інтеграла із наперед заданою точністю (блок схему алгоритму наведено на мал. 26):

Початок.

Крок 1. Задати межі інтегрування [a; b], точність  обліку інтеграла і кількість k вуз­­лів інтегрування.

Крок 2. Розрахувати визначений інтеграл S₂ за формулою Ньютона - Котеса при значенні n = 2.

Крок 3. Покласти S₁ = S₂ і подвоїти кількість вузлів інтегрування (k = k • 2).

Крок 4. Розрахувати визначений інтеграл S₂ за формулою Ньютона - Котеса при значенні n = 2.

Крок 5. ЯкщоS₁ - S₂  , то вважати точність розрахунку досягнутою, ви­вес­ти результати (S₁) на зовнішній пристрій і зупинитися; інакше пе­рейти до кроку 3.

Кінець.