Блок-схема алгоритму методу хорд
1
5
10
2
14
Мал. 17
Ні
13
7
3
4
6
Так
9
8
12
15
16
17
19
11
Так
Так
Ні
f
- початкове
зна-
чення
аргументу; l
- кінцеве
значення
аргументу;
18
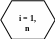
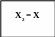
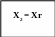
Початок циклу
Кінець циклу
Ітераційний метод Ньютона не потребує визначення інтервалу ізоляції кореня. В основі цього метода лежить розклад функції F(X) у ряд Тейлора:
h2
F(Xn + h) = F(Xn) + h · F'(Xn) + — · F"(Xn) + ...
2
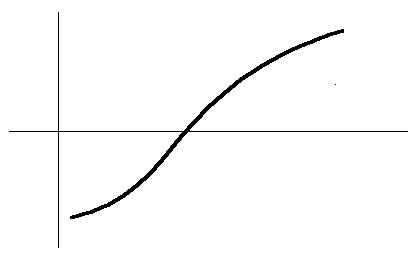
Члени, які містять h, що піднесені до степіні 2 чи вище, відкидаються. F'(Xn) моделюється доторканою (мал. 19).
Y
X
X1
X0
0
X3
X2
Мал. 19
Використовується співвідношення Xn + h = Xn+1. Пропонується, що перехід від Xn до Xn+1 наближає значення функції F(X) до нуля. Тоді:
F(Xn+1) = F(Xn) + F'(Xn) · h = F(Xn) + F'(Xn) · (Xn+1 - Xn) = 0
Потóму, оскільки F'(Xn) · (Xn+1 - Xn) = - F(Xn), то:
F(Xn)
Xn+1 = Xn - ———
F'(Xn)
Якщо |Xn+1 - Xn| > 0,1 · √ ( - задана точність обліку), то ітерації продовжують, причому замість Xn використовують Xn+1. Початкове наближення X0 обирається із умови (F'(X0))2 > F"(X0)·F(X0) >0.
Якщо знаходження похідних F'(X) і F"(X) у методі Ньютона утруднено, то використовують споріднений йому метод «перетинних», у якому F'(X) заміняють виразом (F(Xn+1) - F(Xn)) / (Xn+1 - Xn).
Алгоритм розв’язання системи лінійних рівнянь
З
адача
формулюється
таким чином:
треба знайти
значення {Xi}n,
якi
задовольняють системi
n
лiнiйних
рiвнянь
:
A11 • X1 + A12 • X2 + ... + A1n •Xn = B1
A21 • X1 + A22 • X2 + ... + A2n •Xn = B2
............................................................................. (1)
An-1,1 • X1 + An-1,2 • X2 + ... + An-1,n-1 • Xn = Bn-1
An1 • X1 + An2 • X2 + ... + Ann • Xn = Bn
Метод Гауса полягає у цiлеспрямованому перетвореннi розширеної матрицi коєфiцiєнтiв {Aij, Bi} системи рiвнянь (1) з метою її приведення до три-кутного (мал. 20) вигляду (Aij = 0 для j < i, i [ 1; n]), знаходженнi з останнього рiвняння Xn i обліку {Xi}n-1 зворотньою пiдстановкою визначених змiнних {X} у рiвняння системи (1).
Мал. 20
Алгоритм методу передбачає два етапи розрахункiв: прямий хід і зворотній хід.