«Маленька практика краща за велику теорію» (закон Букера)
Алгоритми розв’язання інженерних задач
Алгоритми розв’язання нелінійного рівняння
Розв’язання нелінійних рівнянь є не тільки важливою самостійною задачею, але і частиною інших задач обчислювальної математики, наприклад, розв’язання нелінійних диференціальних рівнянь або облік власних значень матриць. З ним також пов'язана побудова різноманітних моделей пристроїв і систем опрацювання інформації, інформаційно-вимірювальної техніки.
Трансцендентним рівнянням називається нелінійне рівняння F(X) = 0, що містить тригонометричні або інші спеціальні функції, наприклад, логарифмічні або експоненціальні. Рівняння, що не містить спеціальних функцій, а тільки ступеня аргументу з відповідними коефіцієнтами, є нелінійним алгебраїчним. Всяке значення X*, що звертає функцію F(X) у нуль, називається коренем рівняння.
Використання прямих методів розв'язання нелінійних рівнянь можливо лише для алгебраїчних рівнянь, причому практично доцільно при порядку не більше третього; тому, варто використовувати універсальні ітераційні чисельні методи, які можна реалізувати на комп'ютері і які дають приблизні значення коренів будь-яких рівнянь із наперед заданою точністю. Усі чисельні методи припускають, що рівняння має лише ізольовані корені, або інакше, що для кожного кореня існує інтервал ізоляції [X1; X2], що не містить інших коренів рівняння.
Ітерація знаходження приблизного значення дійсного кореня нелінійного рівняння складається з двох етапів:
ізоляція кореня, або ж пошук сегменту [X1; X2], який містить единий корінь.
уточнення значення кореня на інтервалі ізоляції з заданою точністю.
Ізоляція кореня
Ізоляція кореня практично виконується табулюванням функції F (X) для множини дискретних значень аргументу, отриманою зміною аргументу X із деяким достатньо малим кроком X доти, доки функція не змінить знак на протилежний. Якщо безперервна функція F(X) приймає значення різних знаків на кінцях сегменту [X1; X2] (ознакою цього є виконання F (X1) • F (X2) < 0), то цей сегмент містить корінь X* рівняння F (X) = 0. Графічно це вказує на перетинання графіком функції F (X) вісі абсцис у деякій точці X*, що і є коренем рівняння.
Уточнення значення кореня
Для уточнення значення кореня на інтервалі ізоляції розгляньмо універсальний метод хорд (метод фальшивого становища). Метод хорд полягає у лінійній інтерполяції функції хордою (мал. 16). Хорда проходить через два значення функції у межах інтервалу ізоляції, що мають протилежні знаки, і перетинає вісь абсцис при значенні Xr:
X2 - X1
Xr = X1 - F (X1) • ——————.
F (X2) - F (X1)
Y
X
0
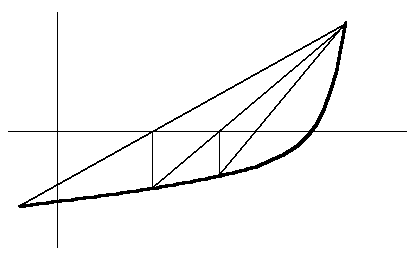
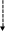
Мал. 16
Значення Xr моделює розташування дійсного кореня X* рівняння на кожній ітерації. Якщо |F (Xr)| > (- задана точність обліку), то ітерації продовжують, розраховують F(Xr) і порівнюють його з F(X1) і F(X2). Надалі в якості однієї з меж інтервалу ізоляції використовують значення Xr:
X2 = Xr, sign F (Xr) = sign F (X2),
X1 = Xr, sign F (Xr) = sign F (X1)
, а значення F (Xr) використовують замість того значення функції, із яким воно збігається за знаком.
Блок-схему алгоритму методу хорд наведено на мал. 17.
Перевагою методу є те, що він породжує оцінки кореня незалежно від вигляду функції і не потребує обліку похідних (як, наприклад, метод Ньютона), хоча іноді і повільно сходиться до результату.
Серед інших методів уточнення значень кореня треба відмітити методи: «дихотомії», Ньютона, «перетинної».
Метод «дихотомії» (мал. 18), передусім, передбачає облік значень функції F(X) на кінцях (X1 і X2) інтервалу визначення функції і у точці Xсер = (X1 + X2) / 2. Значення Xсер моделює розташування дійсного кореня X* рівняння на кожній ітерації. Якщо |F (Xсер)| > (- задана точність обліку), то ітерації продовжують, розраховують F(Xсер) і порівнюють його з F(X1) і F(X2). Надалі в якості однієї з меж інтервалу ізоляції використовують значення Xсер:
X2 = Xсер, sign F (Xсер) = sign F (X2),
X1 = Xсер, sign F (Xсер) = sign F (X1)
, а значення F (Xсер) використовують замість того значення функції, із яким воно збігається за знаком.
λ
λ
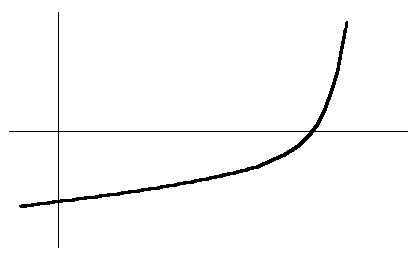
Y
X
X1
X2
Xсер
0
Мал. 18