Блок-схема алгоритму пошуку мінімуму і максимуму

3

4

5

(i>n)

8

1

6

7

2

11

Мал. 11

Так

Ні

Так

Ні

10

9

(i>n)

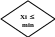
Алгоритми сортування наданих

Нехай задано множину {X_i}_n, елементи якої індексовано довільним чи­ном. Необхідно індексувати{X_i}_n так, щоб із i < j (де i  [1;n], j  [1;n]) випли­вало чи X_i ≤ Xj (упорядкування за збільшенням), чи X_i ≥ Xj (упорядкування за змен­шен­ням).

Аналіз задачі.

Про­цес сортування полягає у послідовних перестановках елементів {Xi}_n доти, доки їхня індексація не узгодиться з їхнім упорядкуванням. Розгляньмо найпростіші алгоритми сортування наданих: метод обміну і метод вибору.

Основна ідея методу обміну (блок-схему алгоритму див. на мал. 12) по­ля­гає у тому, що на кожній i-ій ітерації (i  [1; n-1]) циклу по­рівнюються два су­сі­д­ніх даних X_i і X_i+1. Якщо Xi < X_i+1 (упоряд­ку­вання за зменшенням) або X_i > X_i+1 (упорядкування за збільшенням), то елемен­ти X_i і X_i+1 міняють місцями і ре­­єст­руєть факт такої перестановки прапорцем Prapor = 1 (до того часу Prapor = 0). Таким чином, найменший (найбільший) елемент опиниться на своєму місці у множині {Xi}_n. Після завершення циклу порівняння всіх елементів значення Prapor = 1 є ознакою того, що виконання циклу треба повторити з першої іте­ра­ції, зменшивши кількість ітерацій n на одну. Насправді, в упорядкованій множи­ні не відбу­де­ться жодної перестановки і прапорець Prapor залишить значення 0.

Метод має невелику швидкодію (середня кількість ітерацій складає 1,25• n• n), є малоефективним для великих множин, але ж має найбільш про­зо­рий механізм виконання.

Основна ідея методу вибору (блок-схему алгоритму див. на мал. 13) по­ля­гає у тому, що на кожній i-ій ітерації (i  [1; n-1]) зовнішнього циклу серед еле­ментів {X_j}_n (j  [i+1; n]) шукається індекс k елементу X_k, що є найменшим (упо­рядкування за збільшенням) або найбільшим (упорядкування за зменшен­ням) у порівнянні з елементом X_i. Після цього еле­менти X_k і X_i міняють місця­ми. Метод має трохи більшу швидкодію, ніж метод обмі­ну, оскільки на кожній (i+1)-ій ітерації розглядається множина {X}, менша, ніж на i-ій ітерації, за раху­нок збільшення мінімального індексу множини на 1. У загальному випадку кіль­кість порівнянь даних складає n• (n-1)/2.

Блок-схема алгоритму сортування наданих методом обміну

(за збільшенням)

5

6

7

(i>n)

1

8

Так

Ні

2

4

3

10

Мал. 12

Так

Ні

11

9

Блок-схема алгоритму сортування наданих методом вибору

( за збільшенням)

5

6

7

Мал. 13

Так

Ні

10

11

2

3

8

9

4

1

Алгоритм рекурсивної структури

А ппарат рекурсії є інструментом моделювання абияких об'єктів і про­це­сів реального світу, побудованого загальним методом вкладення фрактально-ре­курсивних структур від мікро- до макрорівня (наприклад, фрактально-рекурсив­ною є система: «елементарна частка  планетна система  галактика  ... »). Наприклад, геометричну фігуру, подібну кожній своїй частині, назива­ють рекурсивною (мал. 14, ліворуч), а зовнішній контур рекурсивної фігури на­зива­ють фракталом (див. мал. 14, праворуч). Кожна деталь фрактала подіб­на повному зображенню у зменшеному масштабі.

Мал. 14

Використання аппарату рекурсії також дозволяє спростити громіздкі ал­горитми розв'язання інженерних і наукових задач.

Алгоритм є рекурсивним, якщо він містить одне чи декілька звернень до самого себе чи до інших алгоритмів, в яких є звернення до такого алгоритму. Під час звернення до звичайного алгоритму вихід з нього завжди трапляється ра­ніше ніж повторний вхід, але для рекурсивного алгоритму це необов'язково. Глибиною рекурсії n називають аргумент рекурсивної функції, який визначає кількість звернень алгоритму до себе. Цей аргумент зменшується на 1 при кож­ному рекурсивному зверненні, а при досягненні самого глибокого рівня рекурсії значення n дорівнює 0, що призводить до термінового звороту керування до ви­кликаючої функції.

Розгляньмо найпоширеніший приклад алгоритму рекурсивної структури -алгоритм обліку факторіалу цілого позитивного числа n:

n! = 1· 2 · 3 · ... · n = (n - 1)! · n

Аналіз задачі.

Алгоритм Factorial (мал. 15) обліку факторіалу цілого позитивного числа

n (треба зауважити, що 0! = 1) звертається до самого себе так, що послідовність

цих викликів виглядає так:

Factorial (n) = n · Factorial (n-1)

= n · (n-1) · Factorial (n-2)

= n · (n-1) · (n-2) · Factorial (n-3)

........................................................................................

= n · (n-1) · (n-2) · ... · 1 · Factorial (1)

= n · (n-1) · (n-2) · ... · 1 · 1

Блок-схема алгоритму обліку N!

2

Алгоритму передається параметр N.

3

Так

1

Мал. 15

Ні

Алгоритм повертає значення Factorial.