Алгоритм циклічної структури (параметр циклу є елементом масиву)
Розрахувати значення функції:
cosXi• e2Y Xi {X1, X2, ... , Xn}10 (n = 10)
Z = ,
3 (sin3Xi - Y) Y = π
, склавши алгоритм циклічної структури.
Аналіз задачі. Якщо sin3Xi = Y, то функція Z=f (Xi,Y) не існує.
Алгоритм (блок схему див. на мал. 8, варіант 1):
Початок.
Крок 1.
Присвоєння значення
змінній
Y.
Крок 2. Введення значення змінної n.
Крок 3. i = 1 (тут i - параметр циклу введення елементів масиву {Хi}n).
Крок
4.
Введення елементу Хi
масиву {Хi}n.
Крок 5. i = i + 1.
Крок 6. Якщо in , то перехід до кроку 4 ().
Крок 7. i = 1 (тут і - параметр циклу обліку значень функції Z (Xi, Y)).
Крок 8. Якщо
sin3Xі
= Y,
то виведення повідомлення «Функція
не існує»
і перехід до кроку 11 ().
Крок 9. Облік значення функції Z (Xi, Y).
Крок 10. Виведення значення функції Z (Xi, Y).
Крок 11. i = i + 1.
Крок 12. Якщо і n, то перехід до кроку 8 ().
Кінець.
Алгоритм розв’язання цієї задачі може бути складено й іншим шляхом (блок схему див. на мал. 8, варіант 2), де цикл введення елементів масиву {Xi}n і цикл опрацювання цих елементів об’єднано в один цикл. У такому варіанті введення елементів масиву {Xi}n буде чергуватися із обліком значень функції мети.
Блок-схема алгоритму циклічної структури (параметр циклу є елементом масиву)
Варіант 1 Варіант 2
1
1
2
2
3
3
(i>n)
5
9
4
Так
4
7
Ні
5
6
8
Так
8
Ні
6
7
Мал. 8
Алгоритм складної циклічної структури
Розрахувати значення функції:
cosX• e2Yi X [Xn; Xk] ; X=α;
Z = ,
3 (sin3X - Yi) Yi {Y1, Y2, ... , Yn}10 (n = 10)
для всіх можливих пар значень аргументів X i Yi функції Z = f (X, Yi), склавши алгоритм складної циклічної структури.
Аналіз задачі. Якщо sin3X = Yi, то функція Z=f (X,Yi) не існує.
Алгоритм (блок схему див. на мал. 9):
Початок.
Крок 1. Введення значень змінних Xn, Xk, X.
Крок 2. Введення значення змінної n.
Крок 3. i = 1 (тут i - параметр циклу введення елементів масиву {Yi}n).
Крок 4. Введення елементу Yi масиву {Yi}n.
Крок 5. i = i + 1.
Крок 6. Якщо і n, то перехід до кроку 4 ().
Крок 7. Присвоювання параметру циклу X значення Xn.
Крок 8. i = 1 (тут i - параметр циклу обліку значень функції Z (X, Yi)).
Крок 9. Якщо sin3X = Yі, то виведення повідомлення «Функція не існує» і перехід до кроку 12 ().
Крок 10. Облік значення функції Z (X, Yi).
Крок 11. Виведення значення функції Z (X, Yi).
Крок 12. i = i + 1.
Крок 13. Якщо і n, то перехід до кроку 9 ().
Крок 14. X = X + X.
Крок 15. Якщо XXk, то перехід до кроку 8 ().
Кінець.
Максимальну кількість Nz значень функції мети Z (X, Yi) можна підрахувати за формулою:
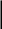Xk
- Xn
Nz = ( + 1) · n
int X