ЛАбы за 1 семестр. Может кому-то понадобятся / Лаба№9(физика)

Лабораторная работа №9

Маятники

Цель работы:

1. Уяснить теоретическое описание колебания математического и физического маятников.

2. Экспериментально установить связь между периодом и длиной математического маятника.

Введение

Ещё в первой половине XVII века Галилей исследовал качания маятника и установил, что их период пропорционален корню квадратному из длины математического маятника. Полное же решение задачи о маятниках выполнено Гюйгенсонсом в 1673 году. Решение этой задачи имело не только исключительное значение для практики изготовления точных часов. Оно в сильной степени способствовало также уяснению принципов динамики, формировавшихся в тот же период.

Мы остановимся на рассмотрении двух частных примеров: математический и простой физический маятники.

Рассмотрим сначала колебания физического маятника. Физическим маятником называется твёрдое тело, которое может начаться под действием силы тяжести вокруг непосредственной горизонтальной оси. Точка пересечения оси качания с вертикальной плоскостью, проходящей через центр масс тела, называется точкой подвеса маятника. На рисунке схематически изображен физический маятник.

Точка подвеса обозначена буквой О. Положение маятника в любой момент времи t можно характеризовать углом отклонения его из положения равновесия φ.

Выведем закон колебания физического маятника, основываясь на уравнении (1)

Связывающим между собой момент силы М относительно неподвижной оси z. С угловым ускорением β и моментом инерции J тела относительно этой же оси. Оно применимо и для физического маятника, качающегося вокруг неподвижной оси. В этом случае М создаётся силой тяжести mg, приложенной в центре масс С. момент силы относительно качания М, равен произведению силы тяжести на плечо h – кратчайшее расстояние от оси качания до направления действия силы тяжести (см. рис.):

(2)

где l_ф - длина физического маятника, она равна расстоянию от точки подвеса О до центра масс С.

Угловое ускорение β, по определению, равно второй производной от угла поворота φ по dt.

(3)

Подставив (2) и (3) в (1), получим:

(4)

Знак минус поставлен потому, что сила тяжести стремиться отклонить маятник в направлении, которое противоположно углу отклонения φ маятника от положения равновесия. При малых углах отклонения (φ<5°= 0,087рад.) можно принять, что φ=sinφ, если φ выразить в радианах. Ограничиваясь в дальнейшем только малыми углами отклонения, перепишем (4) в виде

(5)

Введем обозначение:

(6)

Тогда уравнение (5) можно записать так:

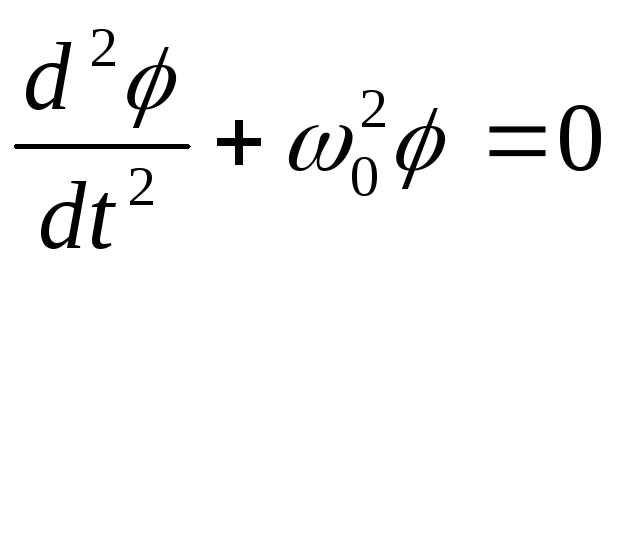
Уравнение такого вида называется уравнением гармонического осциллятора. Оно имеет решение в виде:

Из него следует, что угол отклонения маятника от положения равновесия изменяется по гармоническому закону с круговой частотой ω₀, достигая наибольшего (амплитудного) значения φ₀.

Из (6) следует, что:

Напомним, что круговая частота ω₀ связана с частотой ν(числом колебаний в единицу времени, т.е. ω₀=2πν. Выражение ω₀t+α называется фазой колебания. Оно определяет величину φ в любой момент времени. В частности, при t=0 фаза равна α и называется начальной фазой.

Период полного колебания физического маятника Т – время одного полного колебания выражается через ω₀, как

Подставив сюда выражение для ω₀, получим

(7)

Итак, при малых углах отклонения периода колебания физического маятника прямопропорционально корню квадратному из отношения момента инерции J к длине физического маятника l_ф.

Величину J/ml_ф обозначают l_пр и называют приведённой длиной физического маятника. Это обозначение позволяет придать (7) новый вид:

(7’)

Математический маятник является частным случаем физического маятника. Математическим маятником называется маятник, вся масса которого практически сосредоточена в одной точке – центре масс. Примером математического маятника может служить небольшой шарик, подвешенный на длинной нити. Для такого маятника момент инерции J относительно оси качания равен произведению массы шарика m на квадрат длины нити l², т.е. J=ml². кроме того для него l_ф=l. Подставив в (7) выражения для l_ф и J, получим, что период качания математического маятника, равен:

(8)

Итак, период колебания математического маятника прямопропорционален . График зависимости Т от при этом должен получиться в виде линии, проходящей через начало координат. Угловой коэффициент К этой линии зависит лишь от g и запишется, как

(9)

Сравнивая выражения (7’) и (8), можно приведённой длине физического маятника l_пр придать наглядный смысл. Приведённая длина физического маятника l_пр численно равна длине l такого математического маятника, период колебания которого совпадает с периодом колебания физического маятника.

Если на рисунке вдоль линии ОС отложить l_пр, то получится точка О’, называемая точкой качания физического маятника. Отличительной особенностью этой точки является то, что периоды колебания физического маятника около оси, перпендикулярной ОС и проходящей через О или О’ одинаковы. Физический маятник, имеющий две оси качания, проходящие через точки качания, называется оборотными. Для такого маятника очень легко определить приведённую длину: она равна расстоянии между осями качания.

Ход работы:

Для подтверждения справедливости формулы (8) определили период Т колебания математического маятника для шести различных длин, увеличивая каждую последующую длину. Полученные результаты занесли в таблицу:

l, м	0,6	0,5	0,4	0,3	0,2	0,1
, м1/2	0,8	0,7	0,6	0,5	0,4	0,3
t, c	33	30	25	22	17	13
T, c	1,7	1,5	1,3	1,1	0,85	0,65

Число колебаний приняли за 20 раз. Затем согласно полученным данным построили график зависимости Т от .

Определили теоретическое значение углового коэффициента К, проведенной прямой, по формуле 9.

Выбрали произвольно точку А и нашли её координаты Т и, они равны: 1,1 и 0,5

Теперь по формуле

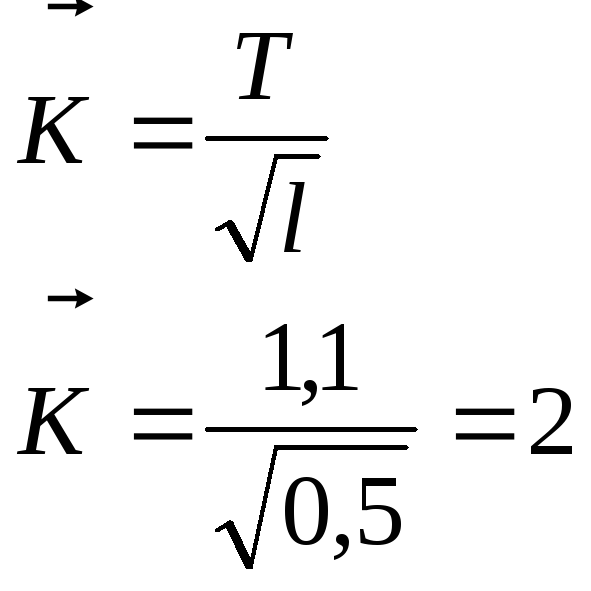
вычислим , для этого подставляем координаты точки А. Учитывая значение и то, что - цена деления, равная 0,1м^1/2, рассчитаем К при практических вычислениях , подставляя наши результаты

Вывод: из графика видно, что у нас получилась прямая, проходящая через начало координат. А это доказывает справедливость формулы 8