1. Критериальный язык описания выбора

Критериальный язык – самый простой, наиболее развитый. Это название связано с основным предположением, состоящим в том, что каждую отдельно взятую альтернативу можно оценить конкретным числом (значением критерия) и сравнение альтернатив сводится к сравнению соответствующих им чисел.

Пусть x– некоторая А из множества альтернатив АX. Считается, что для всехxXможет быть задана функцияq(x), которая называется критерием (критерием качества, целевой функцией, функцией предпочтения, функцией полезности и т.д.) и обладает тем свойством, что если альтернативаx₁предпочтительнее альтернативыx₂(будем обозначать этоx₁>x₂), тоq(x₁)>q(x₂) и обратно.

Предположим, что выбор любой альтернативы А приводит к однозначно известным последствиям (выбор в условиях определённости) и заданный критерий q(x) численно выражает оценку этих последствий, то наилучшей Аx* является та, которая обладает наибольшим значением критерия:

x* = q(x) – для однокритериальной задачи

Сложности решения этой простой по постановке задачи определяются:

• размерностью вектора x;

• характером множества X;

• характером критерия q(x);

и самое главное, сложность существенно возрастает, если (как часто бывает на практике) оценивание А единственным числом является неприемлемым упрощением. Чаще всего необходима оценка А. по нескольким критериям, качественно различающимся между собой. (Например, при выборе конструкции самолёта.).

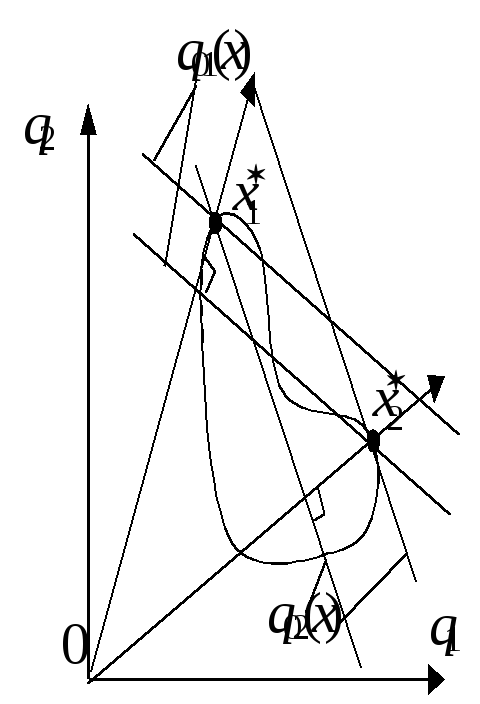
Рис. 1 Рис. 2

Итак, постановка многокритериальной задачи.

Пусть для оценивания А используется несколько критериев q_i(x), i = 1,…,p. Теоретически можно представить себе, что во множестве X окажется одна альтернатива, обладающая наибольшими значениями всех p критериев, тогда она и будет наилучшей. Однако на практике такие случаи почти не встречаются и возникает вопрос, как же тогда оценить выбор (рис. 1, множеству X соответствуют точки фигуры на плоскости значений двух критериев q₁ и q₂, оба критерия желательно максимизировать.

(Линейные комбинации частных критериев работ смысл: чем дальше от нуля, тем лучше).

Рассмотрим наиболее употребительные способы решения многокритериальных задач.

1.1. Сведение многокритериальной задачи к однокритериальной

Это означает введение суперкритерия, т.е. скалярной функции векторного аргумента:

q₀(x) = q₀(q₁(x), q₂(x),…, q_p(x)).

Суперкритерий позволяет упорядочить альтернативы по величине q₀, выделив тем самым наилучшую А (в смысле этого критерия). Вид функцииq₀определяется тем, как мы представляем себе вклад каждого критерия в суперкритерий. Для этого вводят весовые коэффициенты_i, где.

Существуют аддитивные и мультипликативные функции:

;

Тогда задача сводится к максимизации суперкритерия:

x* = q₀(q₁(x), q₂(x),…, q_p(x)).

Недостатки метода: изменение упорядочивающей функции суперкритерия приводит к появлению новой оптимальной А в новом смысле, которая может сильно отличаться от старой (см. рис. 2). Если была функция q₀₁, то  ; но при смене коэффициентов вq₀, например, q₀₂:  ?

1.2. Условная максимизация

Недостатки 1.1. заставляют искать другие подходы. Рассмотрим второй способ решения таких задач. Отметим, что 1 и 2 используются для задач, где частные критерии не равнозначны между собой (разноважные критерии). Идея 2 состоит в выделении главного и рассмотрении остальных как дополнительных, сопутствующих. Такое различие критериев позволяет сформулировать задачу выбора В как задачу нахождения условного экстремума основного критерия

при условии, что дополнительные критерии остаются на заданных им уровнях. На рис. 3 приведено решение задачи

Рис. 3

а) 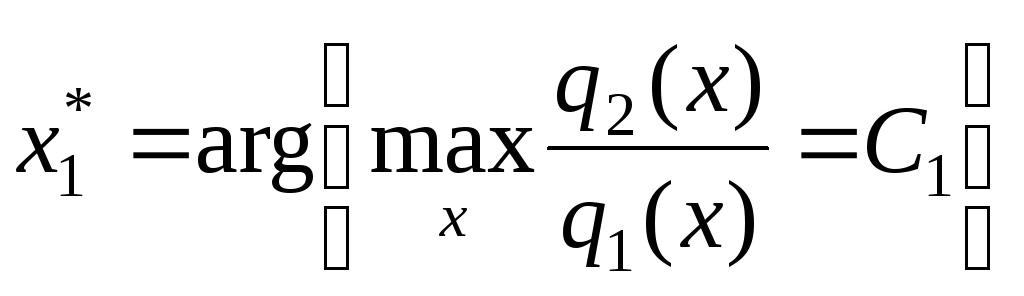– условная оптимизация.

б) оптимизация с нежёсткими ограничениями.

На практике часто оказывается возможным или даже необходимым задавать ограничения на сопутствующие критерии не столь жёстко. Например, если сопутствующий критерий характеризует стоимость затрат, то вместо фиксации затрат разумнее задавать их верхний уровень, т.е. сформулировать задачу с ограничениями типа неравенств:

.

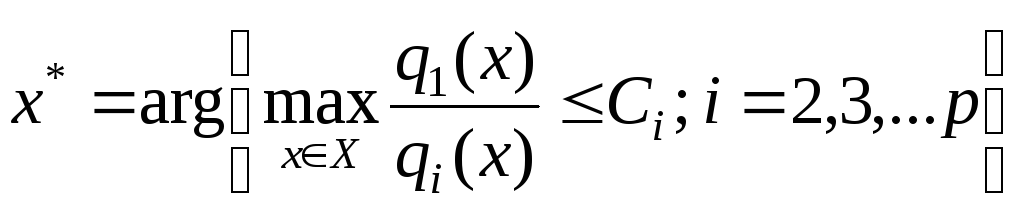На рис. 3 – решение задачи .

в) метод уступок. Пусть частные критерии упорядочены в порядке убывания их важности. Возьмём первый из них и найдём наилучшую А по этому критерию (на рис. 3 это , еслиq₂– самый важный, и– дляq₁). Затем определим уступку Δq_i, т.е. величину, на которую мы согласны уменьшить достигнутое значение самого важного критерия, чтобы за счёт уступки попытаться увеличить, насколько возможно значение следующего по важности критерия и т.д. (на рис. 3и).

1.3 Метод для равноважных критериев.

Поиск альтернативы с заданными свойствами

Этот способ многокритериального выбора относится к случаю, когда заранее могут быть указаны значения частных критериев (или их границы), тогда задача будет состоять в том, чтобы найти А, удовлетворяющую этим требованиям, а если такая отсутствует на множестве Х, найти вХ– такую А, которая подходит к поставленным целям ближе всего. Обсудим некоторые принципиальные моменты данного подхода.

Желаемые значения критериев иногда называютуровнями притязаний, а точку их пересечения в равномерном пространстве критериев – целью, или опорной точкой, идеальной точкой (у разных авторов). Поскольку уровни притязаний задаются без точного знания структуры множества Х, целевая точка может оказаться как внутри, так и вне Х (достижимая и недостижимая цель – на рис. 4 – и ).

Рис. 4

Теперь идея оптимизации состоит в том, чтобы, начав с любой альтернативы, приближаемся к x* по некоторой траектории в пространствеХ. Это достигается введениемчисловой меры близостимежду очередной Аxи цельюx*, т.е. минимизируют расстояния между векторамиq(x)= (q₁(x), q₂(x),…, q_p(x)) и.

4. Нахождение Паретовского множества. Также – для равноважных критериев

Этот способ состоит в отказе от выделения единственной “наилучшей” А, и соглашении о том, что предпочтение одной А перед другой можно отдавать, только если первая по всем критериям лучше второй.

Если предпочтение хотя бы по одному критерию расходится с предпочтением по другому, то такие А признаются не сравнимыми. В результате попарного сравнения А, все худшие по всем критериям А отбрасываются, а все оставшиеся не сравнимые между собой (недоминируемые) принимаются. Если все максимально достижимые значения частных критериев не относятся к одной и той же А, то принятые А образуют множество Парето, и выбор на этом заканчивается.

На рис. 5 жирной линией выделено множество Парето. При необходимости же выбора единственной А следует привлекать дополнительные соображения: новые критерии и ограничения, либо бросать жребий, либо прибегать к услугам экспертов.

Рис. 5

Вывод: многокритериальные задачи не имеют однозначного общего решения. Поэтому предлагается, как мы видели, много разных способов придать многокритериальной задаче частный вид, обладающей единственным решением. Естественно, что для разных способов эти решения являются различными (рис. 5). Поэтому главным в решении многокритериальной задачи является обоснование именно данного (выбранного) вида ее постановки.

2. Язык бинарных отношений (более общий по сравнению с 1)

В реальности дать оценку отдельно взятой А часто затруднительно, однако если рассматривать её не в отдельности, а в паре с другой А, то можно найти основания сказать, какая из них более предпочтительна.

Основные предположения языка:

1) отдельная А не оценивается, т.е. критическая функция не вводится;

2) для каждой пары альтернатив (x, y) некоторым образом можно установить, что одна из них предпочтительнее другой. Либо они равноценны или несравнимы (чаще всего два последних понятия отождествляются);

3) отношение предпочтения внутри любой пары А не зависит от остальных А, предъявленных к выбору.

Существует четыре способа задания отношений:

1. непосредственное перечисление пар – для конечного множества;

2. матричный способ – для конечного множества; матрица отношений определяется элементами:

для всех i, j. Примеры – турнирные таблицы.

3. задание отношения графом; вершины графа G(R) – пронумерованные элементы множества Х, и если – то проводят направленную дугу отк, если же – дуга отсутствует.

4. задание отношения R-сечениями – для бесконечных множеств:

- верхнее сечение отношенияR; (множество всех, которые находятся в отношениис элементом);

- нижнее сечение; (множество всех, с которыми элементхнаходятся в отношении).

Разработана так называемая теория полезности, которая использует при описании выбора язык бинарных отношений. Согласно этой теории возможно по определённым правилам построить некоторую функцию полезности U(x) по определенным правилам, которая позволяет перейти от языка бинарных отношений к критериальному языку.