Глава 3. Обработка результатов измерений

Любые измерения направлены на получение результата, т.е. оценки истинного значения физической величины в принятых единицах. Вследствие несовершенства средств и методов измерений, воздействие внешних факторов и многих других причин результат каждого измерения неизбежно отягощен погрешностью. Качество измерения тем выше, чем ближе результат измерения оказывается к истинному значению. Количественной характеристикой качества измерений является погрешность измерения, определяемая как разность между измеренным х_изм и истинным х_ист значениями измеряемой величины:

dх=х_изм –х_ист , (3.1)

где dx- погрешность измерения.

Результат измерений должен сопровождаться указанием погрешности, с которой он получен.

Погрешность измерений – отклонение результатов измерений от истинного (действительного) значения измеряемой величины.

Достоверность измерений определяется степенью доверия к результату измерения и характеризуется вероятностью того, что истинное значение измеряемой величины находится в указанных пределах. Данная вероятность называется доверительной [7].

Истинное значение физической величины неизвестно и применяется в теоретических исследованиях; действительное значение величины определяется экспериментально из предположения, что результат эксперимента (измерения) наиболее близок к истинному значению величины.

Цель любого измерения – это получение результата измерений с оценкой

истинного значения измеряемой величины. Для этого проводится обработка результатов измерений, в большинстве случаев с помощью вероятностно-статистических методов теории вероятностей и математической статистики.

3.1 Обработка результатов прямых измерений

Пусть результаты n прямых измерений равны . Предположим, что истинное значение измеряемой величины равно a , тогда - погрешность

i-го измерения.

Относительно погрешности предполагаются следующие допущения:

1) - случайная величина с нормальным распределением.

2) Математическое ожидание (отсутствует систематическая погрешность).

3) Погрешность имеет дисперсию , которая не меняется в зависимости от номера измерения, т.е. измерение равноточное.

4) Измерения независимы.

При этих допущениях плотность распределения результата измерения y_i запишется в виде:

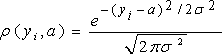(3.1.1).

В данном случае истинное значение измеряемой величины a входит в формулу (2.3.1) как параметр.

Вследствие независимости отдельных измерений плотность распределения системы величин выражается формулой:

(3.1.2).

С учетом (2.3.1) и независимости их многомерная плотность распределения (2.3.2) представляет собой функцию правдоподобия:

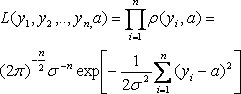. (3.1.3)

Используя функцию правдоподобия (3.1.3) необходимо найти оценку a₀ для измеряемой величины a таким образом, чтобы в (3.1.3) a=a₀ выполнялось условие:

. (3.1.4)

Для выполнения (4.1.4) необходимо, чтобы

. (3.1.5)

По сути условие (3.1.5) является формулировкой критерия наименьших квадратов, т.е. для нормального распределения оценки по методу наименьших квадратов и методу максимального правдоподобия совпадают.

Из (4.1.4) и (4.1.5) можно получить также наилучшую оценку

. (3.1.6)

Важно понимать, что полученная оценка является случайной величиной с нормальным распределением. При этом

. (3.1.7)

Таким образом, получая , мы увеличиваем точность измерений, т.к. дисперсия этой величины в n раз меньше дисперсии отдельных измерений. Случайная погрешность при этом уменьшится в раз.

Для оценки неопределенности величины a0 необходимо получить оценку погрешности (дисперсии). Для этого прологарифмируем функцию максимального правдоподобия (3.1. 3) и оценку дисперсии найдем из условия

(3.1.8)

После дифференцирования получим

, (3.1.9)

а далее, оценку дисперсии : . (3.1.10)

Таким образом мы доказали, что для нормально распределенных данных СКО является лучшей оценкой дисперсии.