
- •3. Расчет подкрановых и тормозных балок
- •3.1 Определение усилий в подкрановой и тормозной балках; подбор сечений подкрановой и тормозной балок и проверка их прочности
- •1. Разработка схемы стального каркаса цеха
- •Определение основных размеров поперечной рамы цеха
- •1.2 Разработка схем горизонтальных связей в плоскости верхних и нижних поясов стропильных ферм; вертикальных связей между фермами и колоннами
- •1.3. Разработка схем продольного и торцового фахверков
- •2. Статический расчет поперечной рамы
- •2.1 Определение нагрузок на раму
- •2.2 Заполнение бланка исходных данных для эвм
- •2.3 Определение невыгодных сочетаний усилий для сечений колонны и анкерных болтов
- •4. Конструктивный расчет колонны
- •4.1 Определение расчётных длин колонны
- •4.2 Расчёт нижней части колонны
- •4.3 Расчёт верхней части колонны
- •4.4 Расчет сопряжения верхней части колонны с нижней
- •4.5 Расчет базы сквозной колонны
- •4.6 Расчёт анкерных болтов
- •5. Расчет ригеля рамы
- •5.1 Определение усилий в стержнях ригеля
- •5.2. Подбор сечений стержней фермы
- •5.3. Расчёт узлов ригеля
- •Литература:
- •Введение
- •Содержание
4. Конструктивный расчет колонны
4.1 Определение расчётных длин колонны

Рисунок 12 – Схемы расчётных длин элементов колонны и приведённые нормальные усилия в ветвях колонны.
При расчете колонн предварительно необходимо установить расчетные длинны нижней и верхней частей колонны в плоскости и из плоскости рамы, а для сквозных колонн и расчетные длины ветвей и элементов решетки в двух плоскостях. Расчетные длины колонн в плоскости рамы определяют по формулам:
![]()
![]() ,
,
где,
lв – длина верхней части колонны, равная 5,23м;
lн – длина нижней части колонны, равная 13,52м.
Коэффициент расчетной длины μ1 для одноступенчатых колонн, закрепленых только от поворота, определябт по таблице 68 СНиПа в зависимости от соотно
шений:
![]()
![]() ,
где
,
где
![]()
Нормальные силы F1 и F2 в сечениях C и A колонны принимают наибольшими по величине и должны соответствовать одним и тем же загружениям. Принимаем F1+F2=2076,1+591,1=2667,2кН, а F2 =591,1кН получим в сечении C из загружения 10.Для определения расчетных длин вычисляем отношения:
![]() ;
;
![]() ;
;
![]() .
.
По таблице 68 СНиПа определим коэффициенты μ1 и μ2:
μ1=1,794;
![]() ,
следовательно принимаем μ2=3.
,
следовательно принимаем μ2=3.
Расчетные длины элементов колонны :
![]()
![]()
![]()
![]()
![]()
![]()
4.2 Расчёт нижней части колонны
Расчет подкрановой (внутренней) ветви.
Расчетное усилие Nв=1740,45кН.
Высота сечения должна
быть:
![]() ,
а также в пределах
,
а также в пределах
![]() .
.
Принимаем h=60см.
Требуемую площадь
сечения ветви определим по формуле,
приняв заранее![]() =0,7:
=0,7:
![]() см2
см2
Внутреннюю ветвь колонны подбираем в соответствии с h и площадью сечения из широкополочных двутавров. Принимаем двутавр 60Б2, со следующими характеристиками и в соответствии с осями: А=145см2, Iу=89320см4, Iх=3720см4, ix=5,07см, iу=24,8см.
Гибкости:
![]() ;
;
![]()
По вычисленным гибкостям ( по наибольшей) определяем φy=0,772.
Проверим общую устойчивость ветви:
![]() ;
;
![]()
общая устойчивость подкрановой (внутренней) ветви обеспечена.
Расчет наружной ветви.
Расчет ведём на усилие Nн =3123,75кН.
Требуемая площадь ветви:
![]() см2
см2
Компонуем ветвь из листа 560х20мм и двух уголков 125х10мм.
Характеристики сечения:
![]() см2
см2
Координаты центра тяжести:
![]() см;
см;
![]() см.
см.
Геометрические характеристики:
![]() см4
см4
![]() см4
см4
![]() см
;
см
;
![]() см;
см;
![]()
![]() ;
;
По наибольшей гибкости находим φу=0,735.
Проверим общую устойчивость ветви:
;
![]()
Устойчивость наружной ветви обеспечена.
Определим центр тяжести всего сечения, где b=bн-z0=150-2,35=147,65см
![]() см
см
Корректируем усилия в ветвях:
![]() кН
кН
![]() кН
кН
Устойчивость наружной ветви проверим повторно:
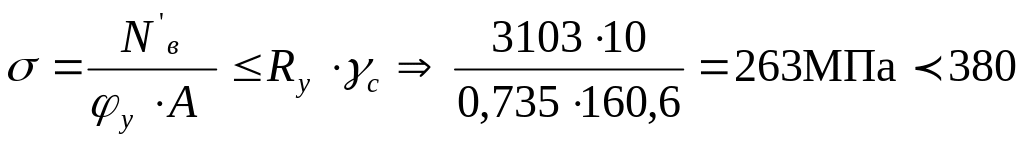 МПа;
МПа;
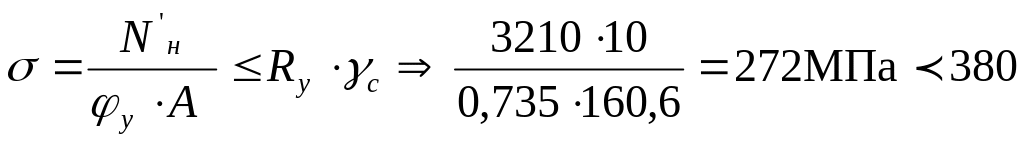 МПа.
МПа.
Устойчивость обеспечена.
Геометрические характеристики всего сечения:
![]() см4
см4
![]() см4
см4
![]() см2
см2
![]() см
;
см
;
![]() см;
см;
![]() ;
;
![]() .
.

Рисунок 13 – Схема сквозной колонны.
Расчет раскоса
Расчёт производим на большую поперечную силу: расчетную Q=243,2кН или условную определяемую по формуле:
![]() ,
,
где,
c – величина, принимаемая по табл. 9: c=12,8;
N – наибольшая сила в нижней части колонны N=2106,5кН.
Коэффициент продольного изгиба определяем по гибкости:
λх=1352/74=18,
откуда φ=0,956.
Следовательно:
![]() кН
кН
Расчетной является сила Q=243,2кН.
Тогда расчетное усилие в раскосе одной системе планок (sinα=1,5/1,75=0,86)
![]() кН
кН
Требуемая площадь
сечения раскоса при φ=0,7
и
![]() =0,75:
=0,75:
![]() см2
см2
Принимаем уголок
110х8мм; A=17,2см2;
imin=2,18см;
![]() ,
откуда φr=0,548
,
откуда φr=0,548
Устойчивость раскоса:
![]() МПа
МПа
устойчивость раскоса обеспечена.
Устойчивость нижней части колонны как целого стержня в плоскости действия момента поверяем по двум расчетным комбинациям усилий. Вычислим приведенную гибкость колонны по формулам:
 ;
;
![]() .
.
Условная гибкость:
![]() .
.
Проверку устойчивости колонны как целого стержня производим в таблице 5.
Таблица 5 – Проверка устойчивости колонны как целого стержня
Формула |
Комбинация №1 усилий |
Комбинация №2 усилий |
N, кН |
2106,5 |
2106,5 |
M, кН∙м |
3105,8 |
3105,8 |
|
1,47 |
1,47 |
|
|
|
|
|
|
|
1,5 |
1,5 |
|
0,321 |
0,303 |
|
|
|
|
|
|

