3. Вопросы к разделу «Случайные величины и числовые характеристики случайных величин»

3.1. Что называется случайной величиной (СВ)?

3.2. Были проведены проверки посещаемости занятий по информатике. При первой проверке обнаружилось, что из 20 студентов присутствуют 15, при второй – 17, при третьей – 13 и т.д. Данные десяти проверок (x_i) сведены в таблицу 3.1. Чему равна средняя посещаемость студентами занятий по информатике?

Таблица 3.1. Данные посещаемости студентами занятий по информатике

№№ проверок	1	2	3	4	5	6	7	8	9	10
xi	15	17	13	20	14	11	19	17	20	18

3.3. Проверяется меткость (попадания в цель) стрелка А. Стрелку выдается пятьдесят патронов. В таблице 3.2. приведены результаты его стрельбы. Согласно этим данным, стрелок один раз попадает в единичку (одно очко), четыре раза – в двойку (двойка - два очка), ... три раза в десятку (десятка – десять очков). Определите статистические вероятности «выбивания» стрелком одного, двух, трех и т.д. очков (заполните третью строку таблицы). Здесь x_i – возможные исходы испытания (стрельбы по мишени), и соответственно частотность и статистическая вероятность попадания в i – й сектор мишени.

Таблица 3.2. Результаты произведенной испытуемым А стрельбы по мишени

xi	1	2	3	4	5	6	7	8	9	10
mi	1	4	6	8	7	7	6	5	3	3
pi

3.4. Сколько очков в среднем выбивает стрелок А одним патроном? Для вычисления используйте формулы (4) и (5).

3.5. Объясните тождественность формул (4) и (5)

(4)

, (5)

где N – общее количество проведенных испытаний (объем выборки).

3.6. Какое свойство случайной величины определяется с помощью формул (6) и (7)

(6)

? (7)

3.7. Аналогичному испытанию подвергается и стрелок В. Результаты его стрельбы приведены в таблице 3.3. Определите статистические вероятности событий x_i, а также среднее значение и величину разброса x_i относительно среднего значения СВ (дисперсию и среднее квадратичное отклонение ).

Таблица 3.3. Результаты испытания стрелка В

xi	1	2	3	4	5	6	7	8	9	10
mi	0	0	7	8	9	10	9	7	0	0
pi

3.8. Объясните выявленное различие между данными испытания стрелков А

и В. Кого бы Вы взяли в команду – стрелка А или стрелка В? Ответ мотивируйте.

3.9. Понятие «математическое ожидание» ( ). Что оно означает?

3.10. При каком условии среднее значение ( ), вычисленное по формуле (4), соответствует математическому ожиданию случайной величины?

3.11. Объясните смысл уравнений

; (8)

, (9)

где - вероятность взятого в круглые скобки выражения (аргумент функции), - сколь угодно малая положительная величина указанной в скобках разности.

3.12. При большом значении N правая часть в формуле (9) будет близка к единице. О чем это говорит?

3.13. По формуле (9) вычислите, при каком значении N вероятность события будет равна 0,95, т. е. .

При определении N используйте дисперсию, вычисленную в задании 3.7.

3.14. Испытание стрелка на меткость (при том же самом числе патронов) может быть проведено в иной форме. Процедура испытания разбивается на несколько серий (допустим, пять либо десять). В каждой серии производится, соответственно, пять или десять выстрелов. Подсчитывается количество очков, выбитых в каждой серии. По ним и производится оценка качества стрельбы.

В таблице 3.4 приведены данные испытания стрелка С. Согласно сведениям, содержащимся в таблице, стрелок С выполняет десять серий по пять выстрелов в каждой серии. Сколько очков в среднем выбивает стрелок С за серию, т.е. используя пять патронов?

Таблица 3.4. Результаты десяти серий опытов по оценке качества стрельбы стрелка С

№№ серий	1	2	3	4	5	6	7	8	9	10
xi	15	36	31	35	42	28	40	45	26	37

3.15. Статистическая обработка данных при указанной в задании 3.15 выборке начинается, как правило, с исключения сомнительного результата. Таковым в данном случае является результат первой серии. Возникает вопрос – не была ли проведена первая серия опытов при отличающихся от других серий условиях? Выяснение этого вопроса осуществляется по следующей схеме:

1. Вычисляют среднее значение случайной величины без учета сомнительного результата (10)

2. Определяют разность

3. Определяют среднее квадратичное отклонение без учета сомнительного результата (11)

4. Находят вспомогательную величину (12)

В рассматриваемом случае вычисления дали следующие результаты: = 35,56,

= 20,56; s = 6,35 и t = 3,24.

Сравним полученное значение с соответствующим теоретическим. Согласно таблице 3.5, при k = 9, теоретическое значение .

Таблица 3.5. Теоретические величины разностей между средним значением и результатом i-того измерения случайной величины для различных n при вероятности β = 0,05

Число измерений (n)	t΄β	Число измерений (n)	t΄β	Число измерений (n)	t΄β
1	2	3	4	5	6
5	0,041	17	2,181	29	2,083
6	2,177	18	2,168	30	2,079
7	2,616	19	2,156	31	2,075
8	2,508	20	2,145	32	2,071
9	2,431	21	2,135	33	2,067
10	2,371	22	2,127	34	2,063

Продолжение таблицы 3.5.

1	2	3	4	5	6
11	2,327	23	2,119	35	2,060
12	2,291	24	2,112	36	2,057
13	2,261	25	2,105	37	2,054
14	2,236	26	2,099	38	2,052
15	2,215	27	2,093	39	2,050
16	2,197	28	2,088	40	2,048

Вычисленное значение больше теоретического, следовательно, предположение о том, что первая серия была проведена в условиях, отличающихся от условий выполнения других серий, подтверждается. Результат первой серии должен быть исключен из рассмотрения.

3.16. Оцените абсолютную и относительную погрешности, допущенные при вычислении среднего количества очков за серию. Используйте формулы (13) и (14).

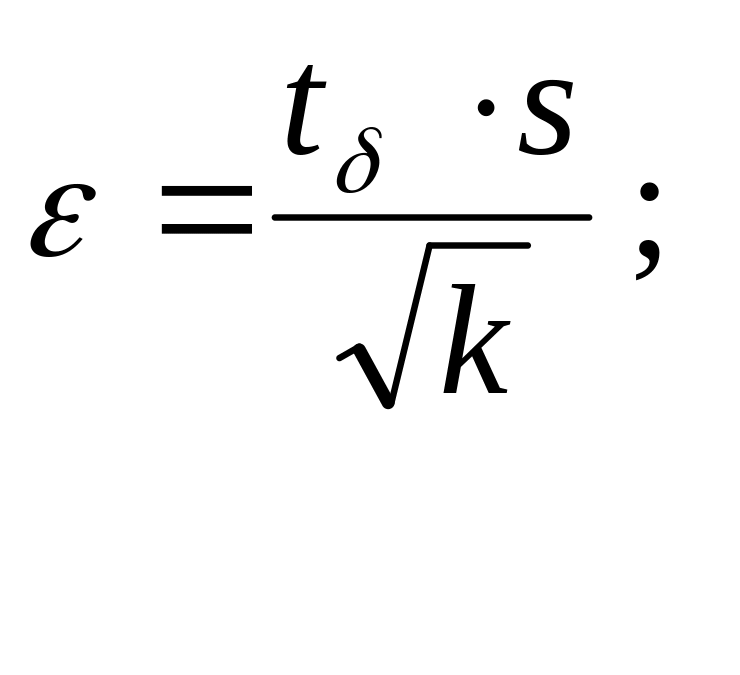(13)

(14)

где коэффициент, зависящий как от числа проведенных опытов, так и от величины доверительной вероятности. В таблице 3.6 приведены значения для каждого конкретного случая. Как следует из таблицы, = 2,31 при k = 9 и доверительной вероятности = 0,95.

3.17. В формуле замените , и их численными значениями. Поясните смысл выражения.

3.18. Заменив в формуле (14) на , а табличную величину её приближенным значением, равным двум, получим

(15)

Какова должна быть величина k (количество серий), чтобы погрешность не превышала 10 процентов, т.е. ? ( )?

Таблица 3.6. Величины , соответствующие конкретным значениям k и доверительным вероятностям .

Число из- мерений k	Значения		Число из- мерений k	Значения
	= 0,90	= 0,95		= 0,90	= 0,95
5	2,132	2,776	20	1,729	2,093
6	2,015	2,571	21	1,725	2,086
7	1,943	2,447	22	1,721	2,080
8	1,895	2,365	23	1,717	2,074
9	1,860	2,306	24	1,714	2,069
10	1,833	2,262	25	1,711	2,064
11	1,812	2,228	26	1,708	2,060
12	1,796	2,201	27	1,706	2,056
13	1,782	2,179	28	1,703	2,052
14	1,771	2,160	29	1,701	2,048
15	1,761	2,131	30	1,699	2,045
16	1,753	2,131	31	1,697	2,042
17	1,746	2,120	41	1,684	2,021
18	1,740	2,110	61	1,671	2,000
19	1,734	2,103	121	1,658	1,980