
- •Введение
- •Техническое задание на типовую курсовую работу*
- •Краткие сведения о модальном управлении
- •Методические указания
- •Выбор основных элементов сау и расчет
- •Выбор электродвигателя
- •Выбор генератора
- •Расчет параметров структурной схемы сау
- •Синтез замкнутой сау
- •Вывод уравнений состояния системы
- •Вывод характеристического полинома системы.
- •Вывод уравнений статистики системы
- •2.4. Расчет коэффициентов обратных модальных связей
- •Расчет переходных процессов синтезированной сау
- •Подготовка данных для расчета на цвм.
- •Расчет и анализ графиков переходных процессов
- •Министерство образования российской федерации
Расчет параметров структурной схемы сау
Суммарное сопротивление якорной цепи, Ом
![]() (1.1.)
(1.1.)
где
![]() - суммарные сопротивления якорных цепей
двигателя и генератора, вычисляемые по
формулам
- суммарные сопротивления якорных цепей
двигателя и генератора, вычисляемые по
формулам
![]() (1.2)
(1.2)
![]() (1.3)
(1.3)
Суммарная индуктивность цепи, Гн
![]() (1.4)
(1.4)
где
![]() - индуктивность якоря двигателя и
генератора, вычисляемые по формулам.
- индуктивность якоря двигателя и
генератора, вычисляемые по формулам.
![]() (1.5)
(1.5)
![]() (1.6)
(1.6)
![]()
Здесь
![]() - угловые частоты вращения двигателя и
генератора
- угловые частоты вращения двигателя и
генератора
![]() .
.
Электромагнитная постоянная времени якорной цепи, c
![]() (1.7)
(1.7)
Конструктивные постоянные двигателя (в системе СИ):
![]() (1.8)
(1.8)
Электромеханическая постоянная времени двигателя, с
![]() , (1.9)
, (1.9)
где
![]() - суммарный момент инерции двигателя и
приводного механизма (при расчете
принять
- суммарный момент инерции двигателя и
приводного механизма (при расчете
принять
![]() ).
).
Постоянная времени обмотки возбуждения генератора, с
![]() (1.10)
(1.10)
Коэффициент передачи обмотки возбуждения генератора, В/А
![]() (1.11)
(1.11)
где
![]() - коэффициент усиления генератора по
напряжению.
- коэффициент усиления генератора по
напряжению.
Кроме указанных параметров структурной схемы, необходимо вычислить следующие величины:
угловую частоту холостого хода двигателя, 1/с
![]() (1.12)
(1.12)
(где ЭДС
генератора
![]() );
);
статическую ошибку (статизм) объекта управления
![]() ; (1.13)
; (1.13)
коэффициент передачи двигателя по управлению
![]() ; (1.14)
; (1.14)
коэффициент передачи двигателя по возмущению
![]() (1.15)
(1.15)
Синтез замкнутой сау
Вывод уравнений состояния системы
Для обеспечения заданных показателей
качества рассматриваемого объекта
(рис.1) достаточно синтезировать три
обратных модальных связи по его физическим
переменным. Наиболее удобными для
практических измерений и преобразований
в управляющие сигналы являются величины
![]() , которые следует принять за переменные
состояния объекта и синтезировать по
ним обратные модальные связи (см. пунктир
на рис.1).
, которые следует принять за переменные
состояния объекта и синтезировать по
ним обратные модальные связи (см. пунктир
на рис.1).
На основании структурной схемы САУ нужно составить операторные уравнения ее элементов и соответствующие им дифференциальные уравнения первого порядка; разрешив эти уравнения относительно первых производных, получим уравнения состояния объекта, которые для удобства дальнейшего использования целесообразно представить в матричной форме
(2.1)
и в соответствующей ей векторной форме
![]() (2.2)
(2.2)
где
![]() - вектор-столбцы переменных состояния
объекта и их производных;
- вектор-столбцы переменных состояния
объекта и их производных;
![]() - постоянные матрицы указанных
размерностей.
- постоянные матрицы указанных
размерностей.
Вывод характеристического полинома системы.
На основании (2.1), (2.2) запишем в компактной форме характеристический определитель системы
,
раскрыв который и выполнив подстановки коэффициентов из (2.1), получим характеристический полином замкнутой системы
(2.3)![]()
где
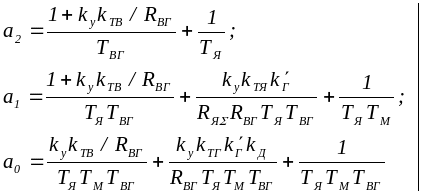 (2.4)
(2.4)
Приравнивая коэффициенты полинома (2.3) к соответствующим коэффициентам выбранного «стандартного» полинома и выполнив ряд несложных преобразований, получаем
 (2.5)
(2.5)
Система (2.5) содержит в качестве неизвестных
три парных произведения искомых
коэффициентов
![]() .
решив эту систему и задавшись одним из
коэффициентов, можно было бы найти
остальные коэффициенты и тем самым
решить традиционную задачу модального
управления. Однако, система (2.5) отражает
требования, предъявляемые лишь к
динамике САУ, поэтому ее нужно дополнить
уравнением, отражающим требования к
статистике САУ.
.
решив эту систему и задавшись одним из
коэффициентов, можно было бы найти
остальные коэффициенты и тем самым
решить традиционную задачу модального
управления. Однако, система (2.5) отражает
требования, предъявляемые лишь к
динамике САУ, поэтому ее нужно дополнить
уравнением, отражающим требования к
статистике САУ.
