6. Точность и погрешность измерений

Из рассмотренных выше примеров мы убедились, что всякое измерение дает лишь приближенный результат, кото­рый в силу множества причин отличается от истинного значения измеряемой физической величины.

Важно иметь в виду, что истинное значение измеряемой физической величины определить абсолютно точно нельзя в принципе. Так, например, значения фундаментальных физических констант постоянно уточняются за счет использования более совершенных методик измерения и измерительной аппаратуры. Каждое последующее уточнение приближает принятое мировым сообществом значение константы к ее истинному значению.

В связи с этим обстоятельством на практике вместо истинного значения используют так называемое действительное значение измеряемой физической величины. Действительное значение – это значение физической величины, полученное экспериментальным путем и столь близкое к истинному значению, что может быть использовано вместо него при решении конкретной реальной задачи измерения. Например, результат измерения массы сахара 1 кг, полученный на исправных и прошедших поверку торговых весах, является в данном опыте действительным значением массы сахара, хотя взвешивание на более точных весах даст другой результат, например, 1,015кг или 0,994кг. Эти значения лишь более соответствуют истинному, и тоже могут использоваться в качестве действительных.

Из сказанного следует, что процедура измерения обязательно должна включать определение и указание степени приближения найденного значения к истинному.

Качественно степень этого приближения характеризуется точностью измерения. Количественная оценка точности есть погрешность измерения. Погрешность есть отклонение результата измерения от истинного (действительного) значения физической величины.

6.1. Абсолютная и относительная погрешности

По виду представления погрешности разделяют на абсолютные и относительные.

Разность между действительным значением физической величины Х и результатом ее измерения х называется абсолютной погрешностью, Δх.

С учетом абсолютной погрешности действительное значение Х записы­вается в виде

.

Абсолютная погрешность выражается в единицах измеряемой вели­чины. Такое представление результата измерения означает, что действительное значение измеряемой величины находится (скорее всего) в пределах от х - Δх до х + Δх, задающих доверительный интервал. Действительное значение X находится внутри этого интер­вала с некоторой – доверительной - вероятностью Р. Доверительная вероятность при технических измерениях задается не менее р = 0,95. таким образом, находят не действительное значение измеряемой физической величины, оценку этого значения в виде границ интервала, в котором находится с заданной вероятностью.

Досмотрим пример. Пусть в результате опыта по определению ускорения свободного падения с помощью математического маятника (см. лабораторную работу №1) получено значение g = 9,7±0,5 м/с². Табличное значение g для средних широт Земли дается как 9,8 м/с^2.. Является ли достоверным полученный результат?

Результат измерения Х_изм считается достоверным, если известное – достоверное – значение измеряемого параметра х₀ принадлежит интервалу Х_изм ∆х, где ∆х – абсолютная погрешность измерения.

В нашем случае Х_изм = g_изм = 9,7 м/с²; ∆х = ∆g = 0,5 м/с².

Х₀ = g₀ = 9,8 м/с².

Изобразим расположение данных на оси g (рис. 23)

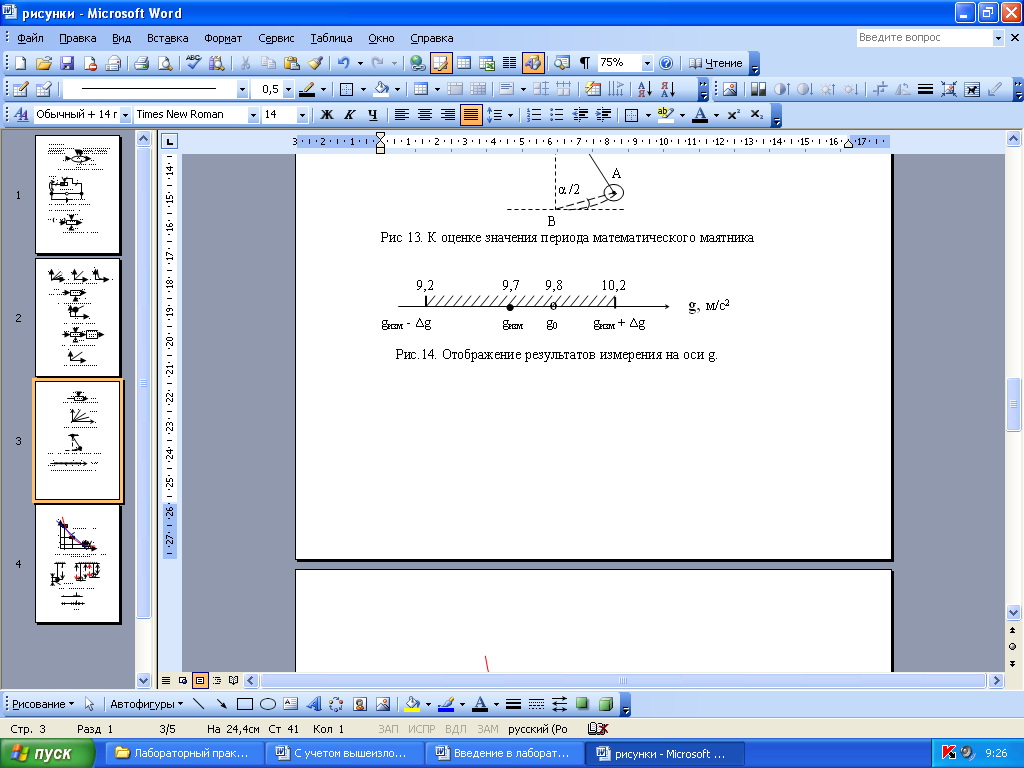
Рис. 23. Отображение результатов измерения на оси g.

Таким образом, результат измерения ускорения свободного падения в данном опыте является достоверным.

Аналогично, если результат измерения температуры представлен в виде Т=273±0,5К, с доверительной вероятностью Р=0,95, это значит, что с вероятностью 95% действительное зна­чение температуры находится в интервале от 272,5 К до 273,5 К.

Чем больше Р и меньше Δх , тем ближе измеренное значение физической величины к действительному (и истинному), т.е. выше точность измерений

.

Абсолютная погрешность не позволяет непосредственно сравнивать результаты измерений по точности. Так, абсолютная погрешность измерения длины Δℓ = 1 м при длине ℓ = 1000 м сви­детельствует о достаточно высокой точности, а при длине 10 м - о низкой. Поэтому кроме абсолютной используется относительная погрешность, определяемая как отношение абсолютной погрешности к результату измерения . Относительная погрешность обычно выражается в процентах.